1. 引言
根据OECD的评估报告,2005~2010年间,经合组织国家的室外空气污染死亡人数下降约4%,但同期中国的室外空气污染死亡人数增加5%,年死亡人数为120多万,年经济损失为1.4万亿美元 [1]。亚洲开发银行与清华大学发布的《中华人民共和国国家环境分析》报告称,中国空气污染每年造成的经济损失,基于疾病成本估算相当于国内生产总值的1.2%,基于支付意愿估算则高达3.8% [2]。另据韩国政府引用安阳大学和水原大学的联合研究报告声称,2011年首尔市PM2.5的污染总量中,来自周边国家的污染占49% (网址:http://politics.people.com.cn/n/2013/1102/c70731-23408272.html),意指中国。中国是以煤为主的能源结构,持续快速的经济增长使中国成为最大的二氧化碳排放国 [3]。“十四五”规划(2021~2025)明确提出:到2025年单位国内生产总值能耗和二氧化碳排放将分别降低13.5%、18%。中国向世界承诺,力争到2030年前实现碳达峰,2060年前实现碳中和,减污降碳协同治理刻不容缓。
PM2.5引发的雾霾天气,是经济长期粗放式增长造成生态赤字的短期集中涌现,产业结构调整战略迫使污染企业从东向西、沿海向内地、城市向农村转移,导致雾霾在城市群间成片连区,笼罩城乡 [4],与实现碳达峰与碳中和目标这一愿景相去甚远。2014年1月4日,中国首次将雾霾天气纳入自然灾情进行通报。但是,空气作为公共物品的性质,导致空气质量的波动不仅与属地系统关系密切,也极有可能受到地缘因素的影响。雾霾所代表的空气质量问题,不仅仅是环境污染问题,更是与自然、经济和社会复合生态系统密不可分的系统问题。相关研究虽广泛,但在讨论雾霾与自然条件的关系时,虽已形成基本共识,即地面气象因素(风速、气温、地面气压、相对湿度等)与雾霾形成显著相关,但大多沿用传统统计方法,将数据看成离散或连续变量,运用面板数据和时序数据进行回归分析,尚缺少大数据、长周期、全地域的系统研究。需要运用基于大数据的函数型数据分析方法和信号分解方法,探讨在近似的气象条件下,空气质量的时空异质性特征及其波动周期,现实意义重大,科学意义明显。
2. 国内外研究现状及发展动态
2012年2月29日,中国环保部废除了空气污染指数(API),确定将空气质量指数(AQI)作为测量空气污染程度的指标 [5]。AQI共考察SO2、NO2、PM10、PM2.5、O3、CO等六方面污染物浓度,除考察细颗粒的危害之外,强调空气中的其他成分也会对人类社会和自然环境造成极大影响 [6]。气象要素和大气污染之间存在密切的相关关系 [7],作为影响空气质量环境重要因素之一,对大气污染物的稀释、扩散、输送和转化过程起制约作用 [8]。1) 与气温的关系。研究发现,空气污染具有典型的季节性特征 [9],气温升高对空气质量好转有显著正效应 [10]。也有研究认为,气温本身对污染物浓度没有太大的影响,是低温带来的采暖需求导致了污染物的排放量增多 [11]。2) 与风速的关系。风速大,大气扩散条件好,污染物稀释能力强,空气质量较好;反之,风速小,大气水平输送能力差,污染物易堆积,空气质量较差 [12]。3) 与气压的关系。地面气压增高有利于空气质量的提高 [13]。4) 与相对湿度的关系。湿度越大,越利于霾的出现和发展 [14]。总体上,风速、温度和气压与污染物日均浓度的相关大于湿度与污染物日均浓度的相关。研究普遍认为,在本地污染源及其排放量相对稳定的情况下,污染物浓度的高低、空气质量的变化主要取决于本地大气的扩散能力 [15]。
上述研究多基于OMI卫星遥感数据,采取描述性数据分析、相关分析主、成分分析等方法对空气污染和气象因素的相关性进行统计分析 [16];或者运用神经网络、模糊数学、支持向量机和计量经济学方法等对大气污染物浓度进行预测 [17]。随着高频海量数据的出现,应用数据挖掘方法,精细化研究大气复合污染的时空特征及关联规律 [18] 是必然趋势。
大数据背景下,当观测时间点十分密集时(如日度数据,小时数据,甚至以分秒为计量单位的数据),例如,脑电信号、基因微序列、股票量价、温度变化和大气污染物浓度等数据 [19],本质上都表现出明显的曲线特征。AQI的实时动态监测,具有显著的大尺度、大数据特征,可以借鉴信号分解的方法,依据数据自身的时间尺度分析空气污染的空间集聚特性和时间波动特征。自然正交函数(EOF)是经典的信号分解技术,通过数据降维来分析变量的时空变化,在气象领域应用比较成熟 [20]。经过EOF正交展开后,特征向量表示空间模态,反映信号的空间分布;主成分代表时间系数,反映信号的时间变化(图1)。由于分解是基于信号序列的局部特性,据此形成的空气污染空间模态分布最近似地还原了污染物在不同区域的聚集程度,具有显著的自适应性 [21]。经过EOF分解出来的时间系数可以反映空气污染随时间波动的趋势。将AQI不同频率的波动逐级分解,产生一系列本征模函数(Intrinsic Mode Function, IMF),反映不同特征尺度波动的波幅随时间变化,具有时域上的局域化特征 [22]。基于EOF的时空分解方法,不必预先设立基函数,在处理非平稳及非线性数据上,具有直观、后验的优势 [23]。
3. 数据来源与研究方法
AQI值基于六种大气污染物,即二氧化硫(SO2)、二氧化氮(NO2)、一氧化碳(CO)、臭氧(O3)、粒径小于或等于10微米的颗粒物(PM10)和粒径小于或等于2.5微米的颗粒物(PM2.5)。
3.1. 数据来源
样本城市在2014年1月1日至2019年12月31日的日AQI值均来自中国国泰君安数据库(CSMAR)。2014年,中国有160个城市进行了空气质量监测1,2015年至2019年的样本城市共335个2。本文“季平均值”指一个日历季内各日平均浓度的算数平均值,“年平均值”指一个日历年内各日平均浓度的算数平均值3。
3.2. 研究方法
3.2.1. Moran’s I
Moran’s I用于检验城市AQI值是否具有空间效应。Moran’s I值在−1到1之间,接近于0说明AQI在空间上随机分布,负值表示负相关,正值表示正相关,其计算公式如式(1)所示 [24]。
(1)
其中
为城市i和城市j的AQI值,n是城市总数,
是空间相关权重,
是样本城市AQI的平均值。本研究采用queen neighborhood rule计算空间权重。如果两个地区接壤,则
;反之,则
。用标准化统计量Z值来检验AQI是否存在显著的空间自相关效应,计算公式如下。
(2)
(3)
(4)
其中
是由Moran’s I组成的空间矩阵,
和
分别是该矩阵的期望和方差。用95%的置信区间检验是否具备显著性。
3.2.2. LISA
LISA指数
是局部莫兰指数,能够检验局部区域内的集聚和分散效应,揭示各城市及其邻近城市的空气质量之间的空间自相关关系 [25],计算公式如式(5)所示。
(5)
式中各符号含义与公式(1)相同,显著性检验也由公式(2)计算。局部空间自相关结果可分为四种类型:高–高型(H-H)、低–低型(L-L)、低–高型(L-H)和高–低型(H-L)。前两种类型在空间上表现为同质性,后两种类型在空间上表现为异质性。
3.2.3. 经验正交函数(EOF)
EOF分析可以对空间数据进行时空分解,识别出主导的空间模态,得到并解释各个模态的变化情况 [26]。特征向量代表的是空间样本,故称为空间模态;主成分则表示为时间变化,称之为时间系数。研究采用EOF分析2014~2019年160个城市AQI值的主要时空分布特征。以160 × 2191日AQI值为矩阵X,将其分解为空间特征向量矩阵EOF和对应时间系数矩阵PC的线性组合,模型构建如下。
(6)
其中,EOF和PC是相互独立的,PC是唯一的时间变量,X的所有时间特征都转移到PC中。
3.2.4. 小波分析
小波分析作为信号处理工具,已成功用于多尺度信息的提取 [27]。一定尺度范围内的局部谱之和表示特定尺度范围内的总方差,用于计算时间序列的周期。小波系数计算如(7)所示:
(7)
其中a是尺度参数,b是相位参数,f(t)是用于分析的信号,
是Ψ的共轭复数。由于时间和频率间的良好平衡性,Morlet小波被用作本研究的母小波函数Ψ。小波系数的方差为:
(8)
研究利用MATLAB的小波分析工具箱进行连续小波变换,以反映时间序列在时间尺度和能量大小上的特征。在某一尺度上小波方差值越大,表明在该尺度上能量和信息越丰富,是主要的特征尺度。
4. 实证结果
研究利用EOF分析将AQI的时间与空间部分进行分离。对于时间部分,利用小波分析识别AQI的波动周期;对于空间部分,通过全局空间自相关、局部空间自相关,分析AQI的空间分异特征。
4.1. 时间特征
用Matlab对AQI进行EOF分析,获得空间模态和对应的时间系数。前三个模态通过了North检验,其中,第一模态的方差贡献率高达86.1%,对应的时间序列可以描述AQI随时间变化的趋势,见图1。第一模态的系数全为正值(图1(a)),说明AQI的变化一致,空气污染以河北省南部为中心,向周边地区逐渐衰减。
 (a)
(a) 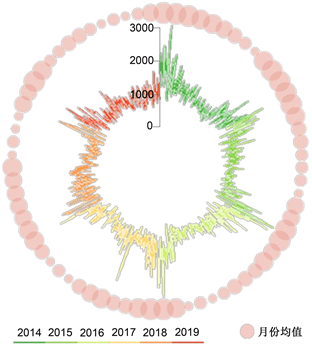 (b)
(b)  (c)
(c)
Figure 1. The first mode of AQI and the corresponding time sequence. (a) First mode; (b) First-mode time sequence; (c) Original plot of the first modal time sequence
图1. AQI的第一模态及对应的时间序列。(a) 第一模态;(b) 第一模态时间序列;(c) 第一模态时间序列原图
时间序列的系数均为正(图1(b)),AQI具有显著的先下降后上升的年度趋势。一年中,AQI的时间序列系数在1、2月份最大,此后波动下降,9月份最低;10~12月份回升。
对AQI第一模态的时间序列进行小波分析,通过峰值对应的主时间尺度来研究AQI的周期变化,如图2。两个主峰分别为562天和273天,说明AQI有19个月的主周期和9个月的第二主周期。
4.2. 空间分异特征
为进一步验证其空间分异特征,用全局空间自相关和局部空间自相关进行分析。全局空间自相关能够衡量AQI的全局空间相关性水平,局部空间自相关能够反映AQI的局部空间特征。
4.2.1. 全局空间自相关
为衡量AQI的全局空间相关性水平,用Moran’s I进行说明,结果见表1。Moran’s I始终大于0,且通过0.001水平的显著性检验,说明AQI存在显著的全局空间正相关效应。

Table 1. Moran’s I of AQI in Chinese cities
表1. 中国城市AQI的Moran’s I
注:表中Moran’s I的均值(mean)、标准差(standard deviation)等值是经过99,999次蒙特卡洛模拟所得,***表示通过0.001的显著性水平。
4.2.2. 局部空间自相关
使用GeoDa绘制莫兰散点图,进一步探究AQI的局部空间特征,如图3。散点在象限I和象限III内较多,说明城市及其邻近地区的AQI多表现为H-H和L-L的同质化聚集特征。
象限I的点表示高AQI的城市被高AQI的城市所环绕(H-H),象限II的点表示低AQI的城市被高AQI的城市所环绕(L-H),象限III的点表示低AQI的城市被低AQI的城市所环绕(L-L),象限IV的点表示高AQI的城市被低AQI的城市所环绕(H-L)。
莫兰散点图难以直观反映空间单元属性与相邻单元相近或相异程度及其显著性,因此,用GeoDa绘制0.05显著性水平下的LISA图来进一步分析AQI的局部空间关联,如图4。H-H和L-L型城市占多数,H-L和L-H型城市占少数,说明相邻区域空气质量存在交互作用。
5. 结论与讨论
5.1. 结论
1) 从时间变化上来看,空气质量指数AQI存在波动周期。一年中,AQI有19个月的主周期和9个月的第二主周期,具有显著的先下降后上升的年度趋势。这种波动周期与自然和人类活动的季节性变化相关 [28]。冬季气温低且降雨少,气压稳定,易出现逆温天气,从而不利于污染物的扩散和稀释;同时冬季淮河以北城市进入供暖期,燃料消费增大,污染排放增多,加剧了空气污染。春秋两季大风天气居多,易引发沙尘,从而加剧了空气污染。因此,时间序列系数在1、2月份最大,此后波动下降。夏季降雨增多,空气湿度增加,有利于污染物的沉积、稀释和扩散,从而改善空气质量,9月份时间序列系数最低,10~12月份回升。
2) 从空间变化上看,空气污染以河北省南部为中心,向周边地区逐渐衰减。总体上,空气污染表现出由南到北、由西到东、由沿海到内陆逐渐加重的空间分异性;此外,空气质量指数AQI存在空间分异特征,从全局空间相关性来看,AQI存在显著的全局空间正相关效应,即AQI指数越高(低)的地区越容易发生聚集现象;从局部空间特征来看,AOI的空间分布变化存在差异,城市及其邻近地区的AQI多表现为H-H和L-L的同质化聚集特征,而H-H和L-L型城市占多数,H-L和L-H型城市占少数,则说明相邻区域空气质量存在交互作用。
5.2. 讨论
从政策启示上看,空气污染不再是单个城市面临的问题,相邻城市间存在较强的空间正相关效应,且存在显著的区域集聚性。因此,为提高空气质量国家及地方政府需要打破行政区域的界限,加强区域合作,将治理方式由城市内部的因地制宜转变为区域联防联控,实现更大空间范围内的全方位区域协同发展。
基金项目
教育部人文社会科学研究青年基金(18YJC630095);
中央高校基本科研业务费专项资金资助(22120210224)。
NOTES
*通讯作者。
1由于莱芜市在2019年1月被撤销并划归济南市管辖,因而2014年的最终样本为160个城市的AQI。
2335个城市覆盖4个直辖市和除海南省的三沙市、儋州市外的所有地级行政区。
3借鉴已有研究和GB3095-2012对AQI平均值的标准定义。