基于粒子群优化算法的模糊PI控制性能研究

Research on the Performance of Fuzzy PI Control Based on Particle Swarm Optimization Algorithm

摘要: 对于传统PI控制系统，其比例常数和积分常数的整定往往依赖于人工经验，在对永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)进行矢量控制时，出现了稳定性不高、控制性能欠佳等情况，于是，提出了模糊PI控制系统。而模糊控制系统中的比例因子和量化因子是经过实验耗费大量时间反复调整取值，随机性大且无法确定最佳的控制器参数，因此，采用粒子群算法来优化模糊控制系统中的比例因子和量化因子，在MATLAB/Simulink中搭建了PMSM整体的矢量控制系统，在不同工况下分析了传统PI控制系统、模糊PI控制系统、基于粒子群优化算法的模糊PI控制系统的调速性能。仿真结果表明，基于粒子群优化算法的模糊PI控制系统，能够有效地缩短调节时间、减小转速的震荡，大幅提升了稳定性。验证了此控制系统能够满足永磁同步电机精度高、输出稳定及快速响应的工作要求。

Abstract: For the traditional PI control system, the adjustment of the proportionality and integration constants often relies on manual experience, and in the vector control of the Permanent Magnet Synchronous Motor (PMSM), the stability is insufficient and the control performance is poor, thus the fuzzy PI control system is proposed. The proportional and quantization factors in the fuzzy control system are adjusted repeatedly after a large amount of time in experiments, which is random and the best controller parameters cannot be determined, therefore, the particle swarm algorithm is used to optimize the proportional and quantization factors in the fuzzy control system, and the overall vector control system of PMSM is built in MATLAB/Simulink. The control performance of the traditional PI control system, fuzzy PI control system and fuzzy PI control system based on particle swarm optimization algorithm was analyzed under various working environments. The simulation results show that the fuzzy PI control system based on the particle swarm optimization algorithm can effectively diminish the regulation time, reduce the speed oscillation and significantly improve the stability. It is verified that this control system can meet the requirements of high precision, stable output and fast response of permanent magnet synchronous motors.

1. 引言

钢铁工业作为国民经济的基础原材料产业，在经济发展中具有重要地位。由于冶金行业复杂多变的生产环境，目前，基于冶金行业的巡检机器人研究较少。上面搭载的红外测温仪、视频摄像头、以及各类传感器、视觉识别功能等工作时，需要巡检机器人保持静止状态，以保证巡检质量，但由于冶金工厂规模大、巡检任务重，巡检效率还远远不能满足实际需求。而永磁同步电机作为巡检机器人动力系统的重要组成部分，其在不同负载、不同坡度下保持稳定运行的特性，能够保证巡检质量的情况下大大提高巡检效率。永磁同步电机(PMSM)是目前工业中使用最为广泛的一种伺服电机，其具有体积小、性能优越、功率密度高、机械特性好以及容易控制等优点 [1] [2] [3]。但是，在永磁同步电机实际运行时，也容易受到内部和外部因素的干扰，所以对永磁同步电机的调速控制系统要求也越来越高。

永磁同步电机是一个非线性且强耦合的负载对象，许多学者基于永磁同步电机的PID控制策略做了大量研究，文献 [4] 采用自适应模糊PID控制，将PID控制与自适应模糊控制相结合，不仅能提高控制效果，而且还能优化控制性能；文献 [5] 对电机实时调速分别采用模糊PID控制和神经网络PID控制方式，实验表明，神经网络在抗干扰方面更具优势，而在实时性方面模糊PID更好；文献 [6] 设计了变论域自适应模糊PID控制器，控制器由双模糊控制器组成，分别负责粗调和微调，与传统PID控制方法相比，抗干扰能力显著提高，具有良好的鲁棒性。基于上述背景，本文为了提高永磁同步电机调速系统的控制效率，针对基于粒子群算法和模糊PI相结合的永磁同步电机调速控制策略进行了深入研究。首先，建立永磁同步电机的基本理论模型，利用粒子群算法对模糊PI控制器进行改进，优化其参数选择和控制，设计基于粒子群算法改进模糊PI的控制系统，并搭建Simulink仿真模型实验平台，进而获得复合控制系统的仿真与实验结果，对基于粒子群优化算法的模糊PI控制系统的有效性进行验证，具有更好的实时性、更短的调速时间、更优良的稳态性能。其结果具有一定的工程实际意义。

2. 永磁同步电机模型的建立

2.1. 矢量控制原理

矢量控制理论是由德国西门子公司的F. Blaschke于1971年提出，矢量控制技术自提出以来，该控制理论就一直在电机控制工程领域中大量使用。矢量控制的基本思想是模仿直流电机的磁场定向方式，以转子磁链方向作为旋转坐标系的参考方向，根据这个坐标系，将定子电流分解为与转子磁链同方向的定子电流励磁分量和与磁链方向正交的定子电流转矩分量。这两个分量相互正交，分别进行调节和控制，从而得到需求的理想转矩。

2.2. PMSM物理模型

永磁同步电机可以理解为定子、转子和转子位置传感器三个部分。定子可以简单认为是绕组，其是电机在运行时不能转动的构件，具体包括三相对称分布的绕组、硅钢片及用来固定铁芯的机壳等部分。转子可以简单理解为磁极铁芯，是电机在运行时可以转动的构件，是永磁电机的关键和核心，具体通常情况下包括磁极铁芯、永磁磁钢、励磁绕组、及磁轭等部分。而转子位置传感器是用来对转子的位置及速度信号进行检测的。由于转子的重要性，我们往往理解的永磁同步电机的结构指的就是转子的结构。电机结构可以进行很多的分类，光是从永磁体方面考虑的，就可以分为表面式和内置式，其是由永磁体不同的转子上安装位置决定。表面式结构采用的是瓦片型永磁体，其附在铁芯的外表面形成径向的磁通，而内置式结构的永磁体是在铁芯的内部。同时，又由于永磁体材料的使用不同，表面式结构可细分为隐极的凸出式和凸极的插入式。凸出式结构的永磁体直接面向气隙，电机交直轴和电感相近，转动惯量小、结构简单、加工和安装简单。相应的插入式结构动态性能以及功率密度都较强，主要是利用了不对称磁路产生了阻磁转矩，但其漏磁极大。两种表面式的转子结构见图1，本文研究的永磁同步伺服系统的执行电机属于表面式中的突出式结构形式。

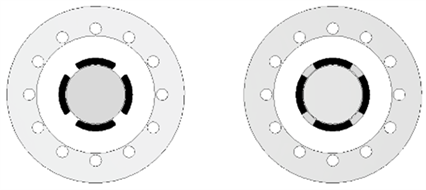
Figure 1. Surface type rotor construction

图1. 表面式转子结构

2.3. PMSM数学模型

三相永磁同步电机(PMSM)是一个强耦合、复杂的非线性系统，为了能够更好地设计先进的PMSM控制算法，建立合适的数学模型就显得尤为重要，建立数学模型时，假设PMSM为理想电机，且满足下列条件。

a) 忽略电机铁芯材料的饱和、涡流、磁滞造成的影响。

b) 不考虑电机参数受温度及频率变化的影响。

c) 电机中的电流为对称的三相正弦波电流。

d) 永磁同步电机为Y形连接，且三相呈2pi/3均匀对称分布。

为了获得静止坐标系的α−β下的基本方程，只需要将同步旋转坐标系d−q下的方程通过反Park变换到静止坐标系α−β即可。旋转坐标系下，其定子电压方程可表示为：

$\{\begin{array}{l}{u}_d=R{i}_d+\frac{\text{d}{\phi }_d}{\text{d}t}-{\omega }_e{\phi }_q\\ u_q=R{i}_q+\frac{\text{d}{\phi }_q}{\text{d}t}+{\omega }_e{\phi }_d\end{array}$ (1)

定子磁链方程为：

$\{\begin{array}{l}{\phi }_d=L_d{i}_d+{\phi }_f\\ {\phi }_q=L_q{i}_q\end{array}$ (2)

式中， $u_d$ 、 $u_q$ 分别是定子电压的d−q轴分量； $i_d$ 、 $i_q$ 分别是定子电压的d−q轴分量；R是定子电阻； ${\phi }_d$ 、 ${\phi }_q$ 为定子磁链的d−q轴分量； ${\omega }_e$ 是电角速度； $L_d$ 、 $L_q$ 分别是d−q轴电感分量； ${\phi }_f$ 代表永磁体磁链。

根据上式可以得出如图2所示的电压等效电路，从图可以看出，三相PMSM的数学模型实现了完全的解耦。

Figure 2. Voltage equivalent circuit of three-phase PMSM

图2. 三相PMSM的电压等效电路

此时，电磁转矩方程为：

$T_e=\frac{3}{2}{p}_n{i}_q\left[i_q\left(L_d-L_q\right)+{\phi }_f\right]$ (3)

将同步旋转坐标系d−q变换到静止坐标系α−β的坐标变换矩阵可表示为：

${\left[f_{\alpha }{f}_{\beta }\right]}^{\text{T}}=\left(\begin{array}{c}\cos {\theta }_e-\sin {\theta }_e\\ \sin {\theta }_e\cos {\theta }_e\end{array}\right){\left[f_d{f}_q\right]}^{\text{T}}$ (4)

经过坐标变换矩阵可得到静止坐标系α−β下的定子电压电流方程：

$\left[\begin{array}{c}{u}_{\alpha }\\ u_{\beta }\end{array}\right]=\left[\begin{array}{c}R+\frac{\text{d}{L}_{\alpha }}{\text{d}t}\\ \frac{\text{d}{L}_{\alpha \beta }}{\text{d}t}\end{array}\begin{array}{c}\frac{\text{d}{L}_{\alpha \beta }}{\text{d}t}\\ R+\frac{\text{d}{L}_{\alpha }}{\text{d}t}\end{array}\right]\left[\begin{array}{c}{i}_{\alpha }\\ i_{\beta }\end{array}\right]+{\omega }_e{\phi }_f\left[\begin{array}{c}-\sin {\theta }_e\\ \cos {\theta }_e\end{array}\right]$ (5)

静止坐标系α−β下的定子磁链方程可表示为：

$\{\begin{array}{l}\frac{\text{d}{\phi }_{\alpha }}{\text{d}t}=u_{\alpha }-R{i}_{\alpha }\\ \frac{\text{d}{\phi }_{\beta }}{\text{d}t}=u_{\beta }-R{i}_{\beta }\end{array}$ (6)

静止坐标系α−β下的电磁转矩方程可表示为：

$T_e=\frac{3}{2}{p}_n\left({\phi }_{\alpha }{i}_{\beta }-{\phi }_{\beta }{i}_{\alpha }\right)$ (7)

FOC矢量定向控制通过Clark变换和Park变换，得到旋转垂直的d−q坐标系，将自然坐标系A、B、C的电流正交分解投影到d−q轴，为i_d，i_q，FOC控制方法有以下四种：

1) 控制D轴电流i_d = 0，电机的转矩只和q轴电流相关，计算出的电机转矩只包含永磁转矩分量，虽然功率因数会随着转矩的增大而减小，但是能保证转矩输出跟随期望设定值。

2) 控制交直轴电流，使得 $\phi =0$， $\cos \phi =1$，这种方法无功功率较小，符合逆变器控制要求，但该方法最大输出的转矩较小，效率低。

3) 对d−q轴电流分量进行配置获得单位电流下的最大电机输出转矩，该方法定子电流小，对逆变器要求较低，可以最好发挥逆变器的功效。

4) 弱磁控制，通过d轴电流磁场与永磁同步电机的气隙磁场相互抵消破坏了电机的平衡状态，若要保持平衡状态则需要对电机进行提速，但是，长时间运行后电机永磁体易退磁，造成不可逆的损伤。

综上所述，对于运行的永磁同步电机，需要调速范围更大，精度更高，i_d = 0的矢量控制方式控制思想简单，易于实现，可以保证充分利用永磁体的磁能，因此，采用i_d = 0的矢量控制方式。

3. 模糊PI控制系统的建立

3.1. PI控制

PI控制是由PID控制发展而来，在电机与电力电子等领域运用较为广泛，二者唯一区别在于微分增益是否存在。因为微分环节往往会导致一定程度的发散，而比例和积分环节已经能够快速调节系统响应，且消除稳态误差，稳定性也得到保障，介于PI控制器已经能够实现相关控制性能，本文设计的永磁同步电机矢量控制系统的电流环和转速环均采用PI控制器来实现 [7]，PI控制系统如图3所示。

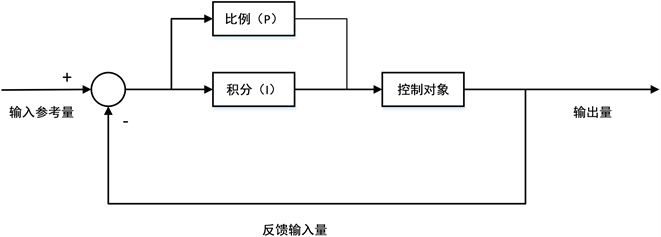
Figure 3. PI control system block diagram

图3. PI控制系统框图

3.2. 模糊控制

模糊控制理论是处理人类语言所特有的模糊信息理论，主要包含模糊集及其隶属函数，模糊算子和模糊关系。模糊控制实质上是一种非线性控制，从属于智能控制的范畴。模糊控制的一大特点是既有系统化的理论，又有大量的实际应用背景。为了实现对电机运动的高精度控制，系统采用全闭环的控制策略，但在系统的速度环控制中，因为负载直接作用在电机而产生的扰动，如果仅采用PI控制，则很难满足系统的快速响应需求。由于模糊控制技术具有适用范围广、对时变负载具有一定的鲁棒性的特点，而电机伺服控制系统又是一种要求具有快速响应性并能够在极短时间内实现动态调节的系统，所以本文考虑在速度环设计了PI模糊控制器，利用模糊控制器对电机的速度进行控制，并同电流环和位置环的经典控制策略一起来实现对电机的精确控制。

模糊控制把设定值和反馈值之间的误差作为输入量，经过模糊控制器将其进行模糊化处理成模糊量，通过专家知识库进行模糊推理，最后对其解模糊化处理成精确量输入控制系统。

3.3. 模糊PI控制器的设计

模糊PI控制器即将增量PI控制与模糊智能控制进行组合，其设计思想首先求出PI控制器的两个参数KP、KI与误差绝对值e与误差变化率绝对值ec之间的关系，运行过程中不断检测误差与误差变化率，根据模糊控制规则不断对参量进行在线调整，来达到不同误差和误差变化率对控制器参数的要求，从而使得被控对象拥有良好的动态性能，模糊PI的控制流程如图4所示。

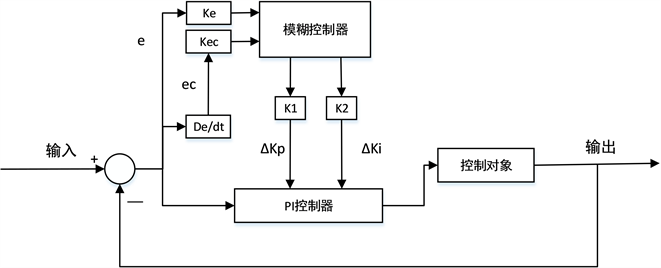
Figure 4. Fuzzy PI control flow chart

图4. 模糊PI控制流程图

经过模糊控制对PI参数的在线调整，实际的Kp，Ki为：

$\begin{array}{l}Kp=K{p}_0+\Delta Kp\\ Ki=K{i}_0+\Delta Ki\end{array}$ (8)

上式中，Kp₀、Ki₀是原PI的控制参数；∆Kp、∆Ki是由模糊控制器生成的补偿量；Kp、Ki是输入被控对象的新PI控制参数；ke、kec为量化因子；k1、k2为比例因子。

模糊控制过程首先将误差(e)和误差变化率(ec)乘以量化因子进行量化；其次，通过模糊化得到E、Ec，而后再有模糊规则库进行推理；最后，反模糊化得到∆Kp、∆Ki。将输入的误差(e)和误差变化率(ec)论域定义为{−3, −2, −1, 0, 1, 2, 3}，输出Kp，Ki论域分别定义为{−0.3, −0.2, −0.1, 0, 0.1, 0.2, 0.3}，{−0.06, −0.04, −0.02, 0, 0.02, 0.04, 0.06}，模糊集合为负大(NB)、负中(NM)、负小(NS)、零(Z)、正小(PS)、正中(PM)、正大(PB)，输入和输出隶属度函数本文选取了三角形隶属函数和Z型隶属函数。其隶属度函数如图5所示。

模糊规则库在模糊推理中至关重要，Kp如果越大，系统的响应速度越快，但是过大容易产生超调，过小响应速度则越慢，Ki若越大则误差消除的越快，过大会产生积分饱和现象，导致产生超调，若过小则系统的稳态误差将难以消除，所以模糊规则是依据专家经验和知识，经过大量实验得出如表1所示。

Figure 5. Membership function diagram

图5. 隶属度函数图

Table 1. ∆Kp, ∆Ki fuzzy rule

表1. ∆Kp、∆Ki模糊规则

以上通过模糊推理得到的是模糊量，给执行机构需要将模糊量转换成精确量，此外去模糊化后的变量是模糊集合论域的清晰值，该论域可能和执行机构所需要的数值范围不一致，因此，输入量进行论域变换，模糊化转化成精确量通常有中位数法(面积评分法bisector)、加权平均法(面积重心法centroid)、最大隶属度法。其中，最大隶属度法如果输出量模糊集合的隶属度函数仅有一个最大值，则取为清晰值，若有多个最大值，通常有平均值法、最大值法、最小值法来获得输出量的清晰值，本文采用的是平均值法，在simulink搭建模糊PI，如图6。

Figure 6. Fuzzy PI control system

图6. 模糊PI控制系统

4. 基于粒子群算法的模糊PI控制系统的建立

粒子群作为智能算法的一种，在1995年，由美国学者在一种鸟群模型中得到启发后提出的，该算法具有易实现、简单、参数比较少并且收敛速度快等优点，一直备受学者们的关注和研究，随着研究的深入，粒子群算法也在越来越多的领域上得到应用。

模糊PI控制系统在永磁同步电机上相比于传统的PI控制系统有较好鲁棒性，对电机的控制比较高效和稳定，且效果显著，但过于依赖专家知识和实验人员的实践经验是模糊PI控制系统的不足，此外，模糊控制系统中量化因子和比例因子的不同取值会影响基本论域不同程度的缩放，从而影响误差控制的灵敏度，而模糊控制系统中的比例因子和量化因子是由人工经验耗费大量时间反复调整取值，随机性大且无法确定最佳的控制器参数，因此，合理地选择模糊控制系统中比例因子和量化因子对于提高控制系统的效果尤为重要，本文采用粒子群优化算法来选取模糊控制系统中的比例因子和量化因子，以此来达到最佳的控制性能。

粒子群算法的基本原理和步骤

粒子群算法是一种受鸟群行为启发的全局优化算法，其中的每一个粒子都可能代表一个解向量，通过跟踪个体最优解和全局最优解来更新速度和位置来实现全局优化 [8]，空间中粒子的相应位置和速度可以表示为：

$V_{id}^{\left(t+1\right)}=w\times V_{id}^{\left(t\right)}+c_1{r}_1\left(P_{id}^{\left(t\right)}-X_{id}^{\left(t\right)}\right)+c_2{r}_2\left(P_{gd}^{\left(t\right)}-X_{id}^{(\; t\; )}\right)$

$X_{id}^{\left(t+1\right)}=X_{id}^{\left(t\right)}+V_{id}^{\left(t+1\right)}$

式中，X_i是粒子i的空间位置；V_i为粒子i的飞行速度； $P_{id}^{\left(t\right)}$ 、 $P_{gd}^{\left(t\right)}$ 分别为t时刻的个体最优解和全局最优解；c₁、c₂为学习因子；w为惯性权重；d为决策变量的维数；r₁、r₂是(0, 1)之间均匀分布的随机数。

粒子群算法优化模糊PI控制流程如图7。

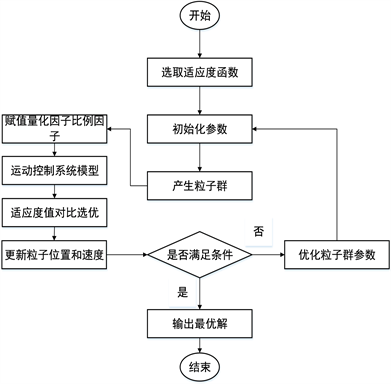
Figure 7. The basic flow of PSO optimizing fuzzy PI parameters

图7. PSO优化模糊PI参数的基本流程

5. 仿真结果及分析

为验证粒子群模糊PI控制的性能，利用 MATLAB 对模糊控制器参数进行寻优，粒子群算法的各项参数设置为：惯性权重ω = 0.6，学习因子c₁ = 1，c₂ = 1，维数D = 5，粒子群规模为30，最大迭代次数为100，最小适应度值为0.1，经过算法优化选取后得到最优的量化因子与比例因子，然后将寻优后的参数导入到Simulink中，调整模糊控制器论域。

设计的目标函数为z = 5 * sys_overshoot/118.0221 + RiseTime/0.0012 + 4 * AdjustTime/0.0024，sys_overshoot为电机转速的超调量，RiseTime为电机超调量时间，AdjustTime是电机从超调量到达目标转速调整时间。经过粒子群算法优化选取最佳的比例因子和量化因子，如何将优化后的参数导入到simulink模型中，调整模糊控制器中的论域，使其达到对电机的优良的控制效果，基于粒子群算法优化的模糊PI控制系统simulink模型如图8。

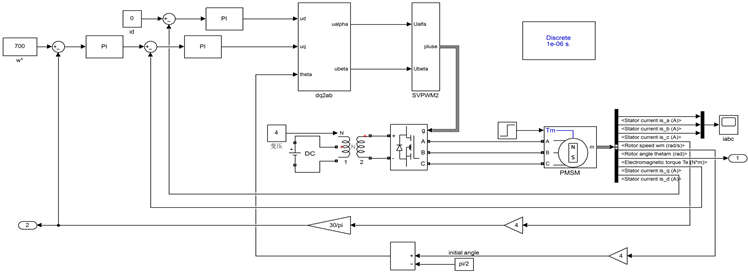
Figure 8. Fuzzy PI control system based on particle swarm optimization algorithm

图8. 基于粒子群算法的模糊PI控制系统

最优个体适应值在大概在第九代趋于稳定，量化因子和比例因子分别对应图6中gain1、gain2、gain3、gain4、gain5，经过粒子群算法优化后得出的值分别为gain1 = 0.5；gain2 = 0.5；gain3 = 0.0653；gain4 = 49.0817；gain5 = 31.8587；适应值优化曲线和比例因子量化因子优化曲线如图9所示。

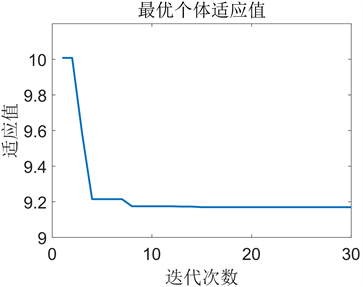
Figure 9. Optimization curve of adaptive value and parameter value

图9. 适应值与参数值优化曲线

基于冶金行业的悬挂轨道式巡检机器人通过搭载仪器仪表实现红外精准测温、可见光视频输助检测功能、视觉识别功能、红外温度传感器、摄像头等精密设备和技术，这些精密的设备要求在运行时巡检机器人的速度波动较小，永磁同步电机在不同工况下保持稳定运行的特性，可以在保证巡检质量的情况下大大提高巡检效率，在simulink中给定电机转速保持稳定在700 r/min，仿真时间为0.04 s，为了模拟不同工况下电机的运行，分别在以下情况中对电机传统的PI控制系统、模糊PI控制系统、基于粒子群算法的模糊PI控制系统进行仿真研究。

1) 设定电机转速700 r/min，仿真时间0.04 s，电机无负载启动，在0.02 s时加入10 N*m负载。

2) 设定电机转速700 r/min，仿真时间0.04 s，电机以5 N*m的负载启动，在0.02 s时负载为0。

仿真结果如图10、图11所示

Figure 10. No load start

图10. 无负载启动

通过比较图10电机无负载启动工况时，为了达到巡检机器人的预定转速，三种控制方法都快速地增加电机转速，超过预定转速后，为了调节超调量，传统PI控制系统调节的转速产生了很大的波动，模糊PI控制系统和基于粒子群优化算法的控制系统产生的速度波动较小，且基于粒子群算法的模糊PI控制系统比模糊PI控制系统和传统PI控制系统调节到预定速度的时间最快。在0.02 s时，加入10 N*m的负载，模拟巡检机器人在轨道上运行时爬坡，由图中转速波形可知，基于粒子群优化算法的模糊PI控制系统产生的速度波动最小，传统PI控制系统产生的波动最大，且基于PSO优化算法的模糊PI控制系统最快。

Figure 11. Load startup

图11. 负载启动

通过比较图11电机负载启动工况，模拟巡检机器人携带取样样品，由速度波形图可知，经过粒子群优化了模糊控制的比例因子和量化因子，其控制产生的速度波动相较于初始的比例因子量化因子波动小，并且调控到达预定转速的时间比模糊PI控制大大地缩短，很快便调节至稳定转速。在0.02 s时，负载突变为0，模拟巡检机器人将样品运送至指定位置卸下，从速度波形图中可知，其波动和调节时间都优于模糊PI控制系统。永磁同步电机参数如表2所示。

Table 2. Simulation parameters of magnet synchronous motor

表2. 永磁同步电机仿真参数

6. 结论

通过模拟不同工况运行得出的仿真波形可知，相较于传统固定增益的PI控制系统与模糊PI控制系统，用粒子群优化比例因子和量化因子后，能够使模糊地输入误差e和误差变化率ec很好地落在论域上，使其控制系统能够有效地缩短调节时间和减小转速的震荡，无论是不加负载启动后突然增加负载还是带负载启动后卸下负载，基于粒子群优化算法的模糊PI控制系统用于永磁同步电机矢量控制时，调速效果更加优良，对于整个系统中的参数变化有更好的适应性，大幅有效地提升了系统的鲁棒性与稳定性。