带熵的随机线性二次最优控制问题

Linear Quadratic Optimal Control Problem with Entropy

摘要: 本文研究了随机线性二次最优控制问题，对带有随机参数的无限时间内的离散时间线性二次最优控制问题，我们不考虑控制过程本身的最优解而是求解控制过程的概率分布，并用熵来度量这个随机概率分布的探索水平。经计算得到控制过程的最优概率分布服从高斯分布，再利用概率分布可求得线性二次型最优控制问题值函数的各项系数矩阵的迭代式。在值迭代的基础上使用Q-learning算法求解各项系数值的平稳解。最后选择两个数值算例证明了Q-learning算法的有效性，并比较了加熵和不加熵时的算法效果，结果表明熵的运用可以使算法收敛更快更稳定。

Abstract: This paper studies the stochastic linear quadratic optimal control problem. For the discrete time linear quadratic optimal control problem with random parameters in infinite time, we do not con-sider the optimal solution of the control process itself, but solve the probability distribution of the control process, and use entropy to measure the exploration level of this stochastic probability distribution. The calculation results show that the optimal probability distribution of the control process obeys the Gaussian distribution. By using the probability distribution, the iterative for-mulas of the coefficients of the linear quadratic optimal control problem value function can be ob-tained. According to the value iteration, Q-learning algorithm is used to solve the stationary solution of each coefficient value. Finally, two numerical examples are selected to illustrate the effectiveness of Q-learning algorithm, and the effect of the algorithm with and without entropy is compared. The results show that the application of entropy can make the algorithm convergence faster and more stable.

1. 引言

线性二次最优控制问题具有非常广泛的应用，在金融、工程等领域有很大的实用价值。Kamlman首先建立了确定性线性最优二次控制理论 [1]，Wonham将此类问题扩展到具有可观察性的确定性参数问题 [2] [3]，Bismut又将问题扩展到参数随机的随机线性二次控制最优问题 [4]。自此，确定性和随机性线性二次最优控制问题被广泛研究。

本文研究的就是随机线性二次最优控制问题。随机线性二次控制优化问题自提出以来，在理论和应用上都得到了快速的发展。Prozaton等人考虑一类参数未知的离散线性系统的二次最优控制问题，利用信息矩阵预测参数的后验不确定性，即后验分布的协方差矩阵，设计了主动自适应控制策略 [5]。在确定性线性二次问题中，成本函数中对应的控制权重矩阵是正定的时候可以通过黎卡提方程求解，很多研究者在研究随机线性最优控制问题时都会假设控制权重矩阵非负定。Chen等人发现对于一些随机线性最优控制问题，即使控制权重项是负的也可以是well-posed，并提出了倒向随机微分方程式的非线性随机黎卡提方程，解决了当权重矩阵是非负定以及不确定情况下的问题 [6] [7]。Rami等人解决了当成本函数中的状态和控制权重矩阵不确定(indefinite)时的有限时间内随机线性二次最优控制问题，通过对原有黎卡提方程放松约束条件和增加新的约束条件引入广义黎卡提方程，并构建出最优控制和最优成本值 [8]。Wang等人基于值迭代使用自适应动态规划算法解决无限时间内的系统动态未知的随机线性二次最优控制问题，并用神经网络识别未知的系统动态以及近似值函数 [9]。Du等人研究了无限时间内随机参数独立同分布的离散线性二次最优控制问题，提出了一种基于Q-learning的迭代算法 [10]。

概率论中熵是不确定性的度量，不确定性越大熵越大。目前在很多方法中都运用了熵。比如强化学习问题中一些方法在目标函数中加上熵。加熵后的强化学习改变了目标函数，但是在探索性和鲁棒性方面提供了实质性改进。比如Ziebart等人所讨论的最大熵策略在面对模型和估计误差时是鲁棒的 [11]。Boularias等人在最大熵框架的基础上介绍了一种新的无模型逆强化学习算法，通过梯度下降方法最小化相对熵来设计算法，并证明了这种方法和已有方法相比有所改进 [12]。Haarnoja等人在最大熵框架下通过获得不同的行为来改进探索 [13] [14]。Zhao等人首先提出了一种基于加权熵的新型多目标强化学习，并开发了一个基于最大熵的优先排序框架来优化所提出的目标。实验显示这种方法在性能和样本效率方面有很好的改进 [15]。Wang等人提出并发展了一种广义熵正则化、松弛的随机控制公式，称之为探索性公式，以明确捕捉强化学习中探索(exploration)和开发(exploitation)之间的权衡。在他的随机控制公式里智能体随机化它的控制来探索和学习环境，经典的控制被控制的分布取代 [16]。同样地，Wang等人在强化学习框架下解决有限时间内连续时间均值方差投资组合问题的时候引入熵来增加探索率，通过探索权重来反应探索和开发之间的权衡，最终实现最佳交易问题 [17]。

在已有的随机线性二次最优控制问题方法的基础上，本文引入熵。对于随机线性二次最优控制问题，目前大部分方法都是根据黎卡提方程或者其他方法直接求最优控制，而本文考虑控制过程的概率分布，即通过求解控制过程的最优概率分布来确定策略，将最优概率分布带入目标函数即可求得随机线性二次型问题各项系数迭代式。数值分析证明了熵的加入使算法收敛更快更稳定。

2. 方法

对于离散时间随机线性二次控制问题，给定初始状态 $x_0=x\in {ℝ}^n$，系统为

$x_{t+1}=A_{t+1}{x}_t+B_{t+1}{u}_t={\Lambda }_{t+1}\left[\begin{array}{c}{x}_t\\ u_t\end{array}\right],t=0,1,2,\cdots ,$ (2.1)

其中 $x_t\in {ℝ}^n$ 代表t时刻的状态， $u_t\in {ℝ}^m$ 代表t时刻的控制。现在考虑折算(discount)问题，其中折现因子 $\gamma <1$，对应成本函数为

$J\left(x,u_{tr}\right)={\displaystyle \underset{t=0}{\overset{\infty }{\sum }}{\gamma }^t\left[x_t^{\text{T}},u_t^{\text{T}}\right]N_{t+1}\left[\begin{array}{c}{x}_t\\ u_t\end{array}\right]}$ (2.2)

其中 $u_{tr}$ 代表控制u的整个轨迹，即 ${\left\{u_t\right\}}_{t=0}^{\infty }$。对应的价值函数定义为

$V\left(x\right):=\underset{u_{tr}}{\min }E\left[J\left(x,u_{tr}\right)\right]$ (2.3)

其中 ${\Lambda }_{t+1}$ 和 $N_{t+1}$ 是随机项，E表示对随机项求期望。

控制过程 $u_t$ 是随机的，可表示为探索和学习，是一个测量值或者分布控制过程，它的密度函数表示为 ${\pi }_t\left(u\right)$。根据贝尔曼最优原则，值函数可以表示为以下形式

$V^{\pi }\left(x\right)=\underset{\pi \in \mathcal{A}\left(x\right)}{\min }{\displaystyle \int {\pi }_t}\left(u\right)E\left[r_t\left(x,u\right)+\gamma V^{\pi }\left(x_{t+1}\right)|x_t=x\right]\text{d}u$ (2.4)

其中 $r\left(x,u\right)=\left[x^{\text{T}},u^{\text{T}}\right]N_{t+1}\left[\begin{array}{c}x\\ u\end{array}\right]$ 是在t时刻控制概率为 ${\pi }_t\left(u\right)$ 下的即时奖励， $\mathcal{A}\left(x\right)$ 是 $x_t=x$ 下的可行性控制分布集(admissible distributional controls)。随机控制过程的概率分布分布可以用 ${\pi }_t\left(u\right)$ 来衡量探索率，可以通过熵来计算它的水平

$\mathcal{H}\left(\pi \right)=-{\displaystyle \int {\pi }_t}\left(u\right)\ln {\pi }_t\left(u\right)\text{d}u$ (2.5)

考虑熵的问题，探索权重用 $\lambda >0$ 表示可以权衡探索和利用(exploitation and exploration)。此时值函数变为

$V^{\pi }\left(x\right)=\underset{\pi \in \mathcal{A}\left(x\right)}{\min }{\displaystyle \int {\pi }_t}\left(u\right)E\left[r_t\left(x,u\right)+\lambda \ln {\pi }_t\left(u\right)+\gamma V^{\pi }\left(x_{t+1}\right)|x_t=x\right]\text{d}u$ (2.6)

如果值函数是有界的，值函数应该是一个二次型形式，假设值函数 $V^{\pi }\left(x\right)=x^{\text{T}}{K}_{2}x+K_{1}x+K_0$， $K_2$ 是半正定矩阵，根据贝尔曼最优原理

$\begin{array}{l}{x}^{\text{T}}{K}_{2}x+K_{1}x+K_0\\ =\underset{\pi \in \mathcal{A}\left(x\right)}{\min }{\displaystyle \int {\pi }_t}\left(u\right)E\left\{\left[x^{\text{T}},u^{\text{T}}\right]N_{t+1}\left[\begin{array}{c}x\\ u\end{array}\right]+\lambda \ln {\pi }_t\left(u\right)+\gamma x_{t+1}^{\text{T}}{K}_2{x}_{t+1}+\gamma K_1{x}_{t+1}+\gamma K_0|x_t=x\right\}\text{d}u\\ =\underset{\pi \in \mathcal{A}\left(x\right)}{\min }{\displaystyle \int {\pi }_t}\left(u\right)E\{\left[x^{\text{T}},u^{\text{T}}\right]\left(N_{t+1}+{\Lambda }_{t+1}^{\text{T}}\gamma K_2{\Lambda }_{t+1}\right)\left[\begin{array}{c}x\\ u\end{array}\right]+\lambda \ln {\pi }_t\left(u\right)+\gamma K_1{\Lambda }_{t+1}\left[\begin{array}{c}x\\ u\end{array}\right]+\gamma K_0|x_t=x\}\text{d}u\\ =\underset{\pi \in \mathcal{A}\left(x\right)}{\min }{\displaystyle \int {\pi }_t}\left(u\right)(\left[x^{\text{T}},u^{\text{T}}\right]E\left(N_{t+1}+\gamma {\Lambda }_{t+1}^{\text{T}}{K}_2{\Lambda }_{t+1}\right)\left[\begin{array}{c}x\\ u\end{array}\right]+E\left(\gamma K_1{\Lambda }_{t+1}\right)\left[\begin{array}{c}x\\ u\end{array}\right]+\gamma K_0+\lambda \ln \pi \left(u\right))\text{d}u\end{array}$ (2.7)

若 $d=n+m$，对于维数为 $d\times d$ 的半正定矩阵P和维数为 $1\times d$ 的矩阵Q，根据下面的划分来引用某些子矩阵

$P=\left[\begin{array}{cc}{P}_{xx}& P_{xu}\\ P_{ux}& P_{uu}\end{array}\right]\text{with}{P}_{xx}\in {ℝ}^{n\times n}$ (2.8)

$Q=\left[\begin{array}{cc}{Q}_{xx}& Q_{uu}\end{array}\right]\text{with}Q\in {ℝ}^{n\times n}$ (2.9)

并定义映射：

$\Pi \left(P\right):=P_{xx}-P_{xu}{P}_{uu}^{+}{P}_{ux}$ (2.10)

$\Gamma 1\left(P,Q\right):=Q_{xx}-Q_{uu}{P}_{uu}^{+}{P}_{ux}$ (2.11)

$\Gamma 0\left(P,Q\right):=-\frac{1}{4}{Q}_{uu}{P}_{uu}^{+}{Q}_{uu}^{\text{T}}++\frac{{\lambda }^{m+1}}{2^{m+1}}\ln \left({\left(2\pi e\right)}^m\det \left(P_{uu}^{+}\right)\right)$ (2.12)

其中 $P_{uu}^{+}$ 表示 $P_{uu}$ 的Moore-Penrose伪逆。令 $M\left(K_2\right)=E\left(N_{t+1}+\gamma {\Lambda }_{t+1}^{\text{T}}{K}_2{\Lambda }_{t+1}\right)$， $M\left(K_2\right)$ 表示矩阵 $K_2$ 的方程。令 $V\left(K_1\right)=E\left(\gamma K_1{\Lambda }_{t+1}\right)$， $V\left(K_1\right)$ 表示矩阵 $K_1$ 的方程。使用上面的符号，并考虑到 ${\pi }_t\left(u\right)\in \mathcal{P}\left(ℝ\right)$，即 ${\displaystyle \int {\pi }_t\left(u\right)\text{d}u}=1$，使用Gateaux导数，可以计算出t时刻控制过程 $u_t$ 的最优概率 ${\pi }_t\left(u\right)$，最终算得最优概率分布为

$\begin{array}{c}{\pi }^{*}\left(u\right)=\frac{\exp \left\{-\frac{1}{\lambda }\left(u^{\text{T}}{M}_{uu}u+u^{\text{T}}{M}_{ux}x+x^{\text{T}}{M}_{xu}u+x^{\text{T}}{M}_{xx}x+V_{uu}u+V_{xx}x+K_0\right)\right\}}{{\displaystyle \int \exp }\left\{-\frac{1}{\lambda }\left(u^{\text{T}}{M}_{uu}u+u^{\text{T}}{M}_{ux}x+x^T{M}_{xu}u+x^{\text{T}}{M}_{xx}x+V_{uu}u+V_{xx}x+K_0\right)\right\}\text{d}u}\\ =\mathcal{N}\left(u|-\frac{M_{uu}^{+}}{2}\left(2M_{ux}x+V_{uu}^{\text{T}}\right),\frac{\lambda }{2}{M}_{uu}^{+}\right)\end{array}$ (2.13)

把 ${\pi }^{*}\left(u\right)$ 带回方程(2.7)，可以得到

$K_2=\Pi \left(E\left(N_{t+1}+\gamma {\Lambda }_{t+1}^{\text{T}}{K}_2{\Lambda }_{t+1}\right)\right)$ (2.14)

$K_1=\Gamma 1\left(E\left(N_{t+1}+\gamma {\Lambda }_{t+1}^{\text{T}}{K}_2{\Lambda }_{t+1}\right),E\left(\gamma K_1{\Lambda }_{t+1}\right)\right)$ (2.15)

$K_0=\frac{1}{1-\gamma }\Gamma 0\left(E\left(N_{t+1}+\gamma {\Lambda }_{t+1}^{\text{T}}{K}_2{\Lambda }_{t+1}\right),E\left(\gamma K_1{\Lambda }_{t+1}\right)\right)$ (2.16)

由此我们可以求得控制过程的最优概率分布以及各项系数的迭代式。现在的问题是当参数是随机的时候如何求得随机线性二次最优控制问题。对于最优控制问题，Bertsekas在他的书里提到了很多强化学习方法 [18]。考虑值迭代的形式，选择使用Q-learning方法。Q-learning算法由Watkins首次提出，是一种基于值的强化学习方法 [19]。一般Q-learning算法中的Q值 $q\left(x,u\right)$ 是关于状态和控制的值，且不容易直接得到，需要用其他方法近似，而本文内我们不直接求状态和控制的Q值而是求了对应值函数的矩阵系数并得到了确定的迭代式，考虑使用Q-learning算法思想，所以仍用Q表示所求值，根据迭代公式定义函数

$Q_2^{*}=E\left[N+\gamma {\Lambda }^{\text{T}}{K}_2\Lambda \right]$ (2.17)

$Q_1^{*}=E\left[\gamma K_1\Lambda \right]$ (2.18)

由此可得

$Q_2^{*}=E\left[N+\gamma {\Lambda }^{\text{T}}\Pi \left(Q_2^{*}\right)\Lambda \right]$ (2.19)

$Q_1^{*}=E\left[\gamma \Gamma 1\left(Q_2^{*},Q_1^{*}\right)\Lambda \right]$ (2.20)

所以最终 $K_2=\Pi \left(Q_2^{*}\right)$， $K_1=\Gamma 1\left(Q_2^{*},Q_1^{*}\right)$。K₂和K₁是Q₂和Q₁矩阵的子矩阵划分，因此可以先求得Q₂和Q₁，由此设置算法1 (表1)：

Table 1. Q-learning algorithm for stochastic linear quadratic optimal control

表1. 随机线性二次最优控制的Q-learning算法

其中学习率满足 $\underset{t=0}{\overset{\infty }{{\displaystyle \sum }}}{\alpha }_t=+\infty$， $\underset{t=0}{\overset{\infty }{{\displaystyle \sum }}}{\alpha }_t^2<+\infty$。由于参数是随机的，所以对于算法中的期望部分使用蒙特卡洛方法计算，即 $\frac{1}{s}\underset{k=1}{\overset{s}{{\displaystyle \sum }}}\left[N_k+\gamma {\Lambda }_k^{\text{T}}{Q}_2\left(t\right){\Lambda }_k\right]$。

3. 数值分析

为了验证算法的可行性和有效性，进行数值分析。目前已知所求值的迭代公式，所以可以根据迭代公式直接求目标值，因此先比较根据迭代公式求解和根据Q-learning算法思路求解的不同。两种方法结果如图。

根据图1可以看出直接根据迭代公式用迭代法求解的目标值一直有较大的波动，且在迭代次数范围内并不收敛。而本文选择的Q-learning算法求得的目标值比迭代法求得的目标值更准确且最终收敛。由此可以说明本文采用的Q-learning算法有一定的优势且更有效。

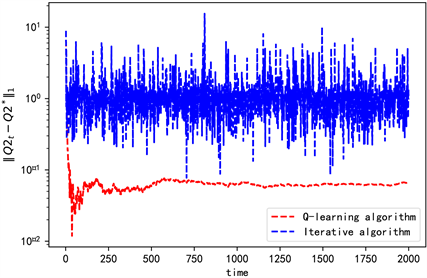
Figure 1. The comparison of iterative algorithm and Q-learning algorithm

图1. 迭代算法和Q-learning算法的比较

本文和其他方法最大的区别在于在目标函数中加入了熵，因此在数值分析过程中主要考虑值函数加熵和不加熵即 $\lambda \ne 0$ 和 $\lambda =0$ 两种情况，对于 $\lambda \ne 0$ 时需要考虑 $\lambda$ 取不同值时的情况。比较 $\lambda =1$ 、 $\lambda =5$ 和 $\lambda =10$ 时Q₂的收敛情况，

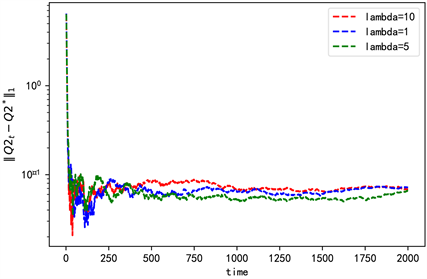
Figure 2. The convergence with different explore weight

图2. 探索权重不同时的收敛情况

由图2可知选取的3个不同的 $\lambda$ 对应的收敛以及稳定情况大致相同，最后选择 $\lambda =1$。令折扣因子，算法中的学习率，在蒙特卡洛计算期望值是使。

首先考虑状态空间，控制空间时的情况。此时使 ${\Lambda }_t={\Lambda }^{\left(0\right)}+{\omega }_t^{\left(1\right)}{\Lambda }^{\left(1\right)}+{\omega }_t^{\left(2\right)}{\Lambda }^{\left(2\right)}$，，其中，独立同分布且服从标准正态分布。

${\Lambda }^{\left(0\right)}=\left[\begin{array}{ccc}-1& -0.1& -0.2\\ 2.6& 0.5& 0.5\end{array}\right]$， ${\Lambda }^{\left(1\right)}=\left[\begin{array}{ccc}0.6& 0.075& 0.125\\ -0.8& 0.1& -0.375\end{array}\right]$

${\Lambda }^{\left(2\right)}=\left[\begin{array}{ccc}-0.06& -0.06& 0.02\\ 0.2& 0.23& -0.09\end{array}\right]$， $N^{\left(0\right)}=\left[\begin{array}{ccc}3.11& 1.5626& -0.2798\\ 1.5626& 1.816175& -1.021425\\ -0.2798& -1.021425& 0.91585\end{array}\right]$

得到各迭代值收敛情况为(图3~5)。

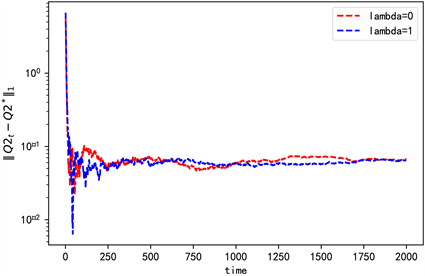
Figure 3. The convergence of Q₂ when n = 2

图3. n = 2时Q₂的收敛情况

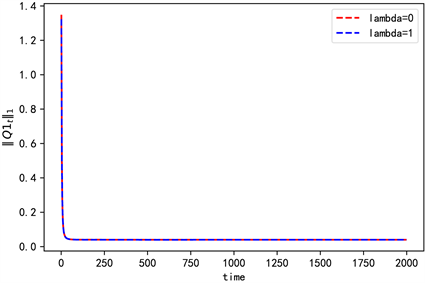
Figure 4. The convergence of Q₁ when n = 2

图4. n = 2时Q₁的收敛情况

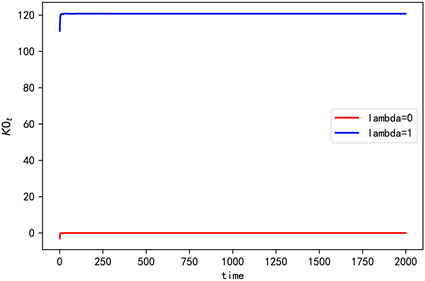
Figure 5. The convergence of K₀ when n = 2

图5. n = 2时K₀的收敛情况

然后考虑状态空间，控制空间时的情况，令，其中标准正态分布。

${\Lambda }^{\left(0\right)}=\left[\begin{array}{cccc}-0.7718& 0.3632& 0.1619& 0.7298\\ 0.0335& 0.1955& -0.0709& 0.3275\\ -0.0738& 0.2609& 0.5275& -0.5730\end{array}\right]$，

${\Lambda }^{\left(1\right)}=\left[\begin{array}{cccc}-0.4505& 0.0671& 0.1783& 0.1651\\ -0.900& -0.0628& -0.1045& -0.4122\\ -0.6539& -0.4185& -0.2444& 0.9814\end{array}\right]$，

得到各迭代值收敛情况为(图6~8)。

由一次项和常数项系数值可以看出，此时在值函数中加熵不会影响他们的收敛情况，但是加熵后存在数值差异，且集中在常数项。由图3和图6可知，加熵后对应的二次项系数收敛更快更稳定。

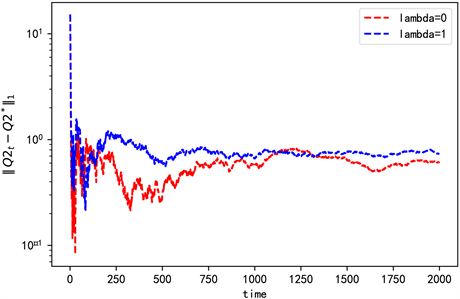
Figure 6. The convergence of Q₂ when n = 3

图6. n = 3时Q₂的收敛情况

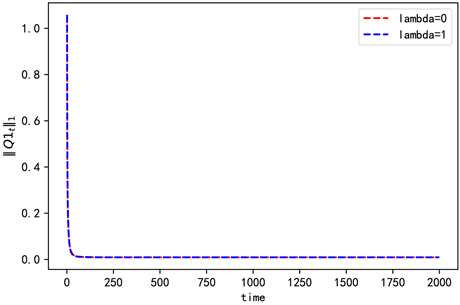
Figure 7. The convergence of Q₁ when n = 3

图7. n = 3时Q₁的收敛情况

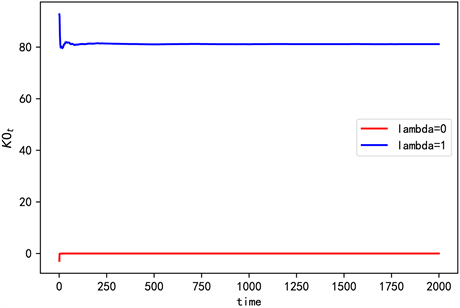
Figure 8. The convergence of K₀ when n = 3

图8. n = 3时K₀的收敛情况

4. 结论

对于确定性和随机性线性二次最优控制问题，目前很多方法都是围绕着黎卡提方程求解最优控制过程，本文不直接考虑控制过程，而是考虑控制过程的概率分布，同时用熵来表示控制过程的探索水平。在原来的目标函数上加熵，对加熵后的目标函数关于概率分布求Gateaux导数得到控制过程的最优概率分布，并化简得到控制过程最优概率分布服从高斯分布。将概率分布带回加熵后的目标函数求出线性二次函数的各系数的迭代公式，使用蒙特卡洛算法计算期望值，最后用Q-learning算法得到各系数的最终平稳值。比较直接用迭代公式求解和用本文使用的Q-learning算法求解的结果，证明了本文算法有一定的优势且更有效，两个数值分析证明了算法的收敛性，同时表明了加熵后改变了目标函数值的大小，但是差值主要集中在常数项，也证明了熵的运用使算法收敛更快更稳定。

致谢

感谢导师给的建议和指导以及师兄师姐师弟师妹们的鼓励和帮助。