基于ABAQUS的电子助力器副密封圈参数优化

Parameter Optimization of Seal Ring of Elec-tronic Booster Pair Based on ABAQUS

摘要: 电子制动助力器作为线性控制系统的一种解决方案，对结构可靠性提出了更高的要求，其中制动主缸密封皮碗的失效问题严重影响着制动总缸的抗失效性能。着眼于上述问题，本文以密封皮碗的材料形状、组装要求等参数设计正交试验，运用Abaqus模拟密封皮碗在位移下的受力过程并求出挤入处的最大Mises应力、挤入量和左侧密封处的磨损量；建立了影响因素与响应的二次响应回归方程；以密封皮碗防啃噬、防磨损相关效果为优化目标，使用遗传算法NSGA-II相关函数进行多目标优化，结合原尺寸结果挑选出帕累托最优解，使密封圈的抗失效性能得到了提高。

Abstract: As a solution of linear control system, electronic brake booster puts forward higher requirements for structural reliability, and the failure of the brake master cylinder seal bowl seriously affects the anti-failure performance of the brake master cylinder. In view of the above problems, the orthogo-nal test was designed with the parameters of the material shape and the assembly requirements of the seal bowl. Abaqus was used to simulate the stress process of the seal bowl under displacement and the maximum Mises stress, the extrusion amount and the wear amount at the left seal were obtained. The quadratic response regression equation of influencing factors and response was es-tablished. With the anti-gnawing and anti-wear effect as the optimization objective, NSGA-II corre-lation function of genetic algorithm was used for multi-objective optimization, and the Pareto opti-mal solution was selected based on the original size results, which improved the anti-failure per-formance of the seal ring.

1. 引言

随着汽车线控技术的研究发展，电子制动助力器由于其控制精度高、响应迅速、布置灵活的特点，广泛应用于各类新能源车辆的制动系统中 [1]。作为线控制动系统的关键安全部分，电子制动助力器的可靠性和耐久性对车辆的平稳运行起到重要的影响。而主缸密封圈作为电子助力器的核心部件，其工作原理是在活塞转换成液压能的过程中分隔压强并密封，涉及到一系列液压作用、材料超弹性等问题。在常规制动工况下，制动主缸缸内压强在90~100 bar左右。在长期使用过程中，主缸密封皮碗会受到活塞、油液冲击的影响继而发生磨损，导致密封失效。此外，密封圈的底部会因摩擦、液压作用而被挤入活塞与缸体的间隙中，导致其底部的局部应力集中，在运行中不断累积，最终导致密封圈底部的啃噬失效 [2]。

至今，国内外的高校和企业针对密封皮碗的失效形式提出了许多研究以及解决方案。Dodds等人研究EPDM橡胶制成的密封圈，研究发现当压力升至一定时，密封圈会其形状的问题，最后导致破裂。这一现象影响了密封圈性能，失效问题主要是由于EPDM橡胶材料的特性 [3] [4] [5] [6]。

本文以某电子助力制动器的主缸密封皮碗为研究对象，以防啃噬、防磨损为优化目标，结合硬度、摩擦系数、间隙距离等相关变量，开展了密封皮碗参数优化，得到最佳的密封皮碗参数组合，对电子制动助力器的可靠性具有重要的意义。

2. 理论模型

2.1. 橡胶材料本构模型参数

本文制动主缸密封皮碗采用的材料为EPDM橡胶 [7]，相应使用的是Mooney-Rivlin本构模型。Mooney-Rivlin本构模型针对有着高度非线性的应力应变曲线的橡胶材料，常用应变能密度函数来表征橡胶材料的超弹性 [8]，进而可以较好地表现橡胶材料在中小应变作用下的特性，其式为：

$U=C_{10}\left(I_1-3\right)+C_{01}\left(I_2-3\right)$ (1)

式中：U表示应变能密度； $C_{10}$ 、 $C_{01}$ 为橡胶材料的力学性能常数； $I_1$ 、 $I_2$ 为第一和第二应力不变张量。

$I_1={\sigma }_1^2+{\sigma }_2^2+{\sigma }_3^2$ (2)

$I_2={\sigma }_1^2{\sigma }_2^2+{\sigma }_2^2{\sigma }_3^2+{\sigma }_1^2{\sigma }_3^2$ (3)

式中： ${\sigma }_1$ 、 ${\sigma }_2^2$ 和 ${\sigma }_3^2$ 分别为橡胶沿x、y、z方向的主应力。

通过指定的橡胶硬度，计算出相应的弹性模量，相关公式如下：

$E=\frac{15.75+2.15H_S}{100-H_S}$ (4)

式中： $H_S$ 为橡胶邵氏硬度。

将计算出的弹性模量带入，得到相应的橡胶力学性能常数，相关公式如下：

$C_{10}=0.25C_{01}$ (5)

$C_{01}=\frac{E}{6\times 1.25}$ (6)

$D_1=\frac{1-2\gamma }{C_{10}+C_{01}}$ (7)

式中：泊松比 $\gamma$ = 0.499。

综上，通过以上公式，得到的橡胶材料参数如表1所示。

Table 1. Rubber constitutive model parameters

表1. 橡胶本构模型参数

2.2. 啃噬失效

本文主要针对某型电子制动助力器制动主缸的副密封皮碗进行研究，其制动缸采用的是双腔式的构造 [9]。电子制动助力器采用空心滚珠丝杠机构，通过齿轮的传动将电机扭矩输出，继而用活塞将推杆传递过来的能量进行转换，继而由旋转到平动。制动主缸的结构一共包含4个密封皮碗，其中第二活塞密封圈又称副皮碗，如图1所示，是制动主缸重要的密封机构。副皮碗一旦发生故障，就会导致外界气体进入制动主缸内，出现漏液，变质的问题，进而腐蚀缸体以及降低电子制动助力器的性能，导致汽车刹车系统的可靠性变差。

Figure 1. 3D model of sub-leather bowl

图1. 副皮碗三维模型

根据电子制动助力器的常规制动工况 [10]，制动缸内压力一般在90 bar左右，在极端工况下可达130 bar以上。在这种载荷的长期作用下，会发生接触面的磨损，导致密封皮碗的断裂以及疲劳失效，继而密封性能下降。在高压作用下，易变形的橡胶材料会被挤入密封间隙中，如图2所示。底部被挤入间隙后，局部应力变大，并随着活塞的往复运动和工况的不断影响下加剧，甚至导致底部被缸壁切除，导致密封皮碗的啃噬失效 [11]。

Figure 2. Diagram of gnawing failure

图2. 啃噬失效示意图

密封皮碗的底部被切除，是因为油液压力过大以及橡胶材料硬度过低，导致了密封皮碗啃噬的发生，实际需考虑摩擦系数和橡胶硬度对密封皮碗啃噬的影响，这里为了定量表示密封圈啃噬现象的程度，引入挤入量d来描述密封圈底部被挤入缸壁间隙的距离，如图3所示。

Figure 3. Diagram of squeeze volume

图3. 挤入量示意图

2.3. 磨损失效

磨损作为一种常见的失效形式，对电子制动助力器密封圈的密封性能都有很大的影响。基于Archard理论模型 [12]，对密封圈的受损情况进行分析，则可得到密封圈材料的磨损深度h：

$h=K\frac{p_m}{H}S$ (8)

式中： $h$ 为密封圈磨损深度，单位mm； $p_m$ 为密封圈接触应力，单位Mpa。

在密封圈收到活塞运动以及时间的影响下，式(8)进一步变为：

$\text{d}h=K\frac{p_m\left(t\right)}{H}v\text{d}t$ (9)

$v=\frac{d}{2}$ (10)

式中： $v$ 为活塞速度，单位mm/s； $d$ 为活塞位移，单位mm。

密封圈的磨损寿命N是磨损深度H和单次磨损深度的比值，本文不进行寿命预测，只是通过这种方法对磨损失效进行定量分析。以上是密封圈磨损模型的建立，无量纲磨损系数为 $\text{K}=1.22\times {10}^{-8}$。

3. 有限元计算

3.1. 密封圈有限元模型建立

1) 材料属性

目前，主缸密封圈多使用三元乙丙橡胶(EPDM)作为制动缸密封圈的材料。橡胶材料的应力应变曲线具有高度非线性的特点，在实际项目方面普遍采用应变能密度函数来表现橡胶材料的超弹性。常见的本构模型有Neo-Hookean模型、Yeoh、Polynomid-Form模型、Mooney-Rivlin模型模型等。研究表明，Mooney-Rivlin本构模型的可用表现较好，更贴近本文研究。

密封圈的最内侧内径为21.8 mm，最外侧直径为30.5 mm，截面大致为V型，如图4所示，橡胶材料为三元乙丙橡胶(EPDM)。

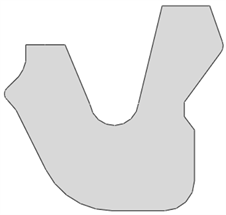
Figure 4. Section diagram of 2-d seal ring

图4. 2维密封圈截面图

橡胶密封圈作为超弹性体，体积不随运动变形而变化，设泊松比为0.5。缸壁和活塞的弹性模量远大于橡胶密封圈，因此视缸壁和活塞为刚体。

密封圈的单元类型是CAX4RH，适用于橡胶材料的中小变形分析，缸壁和活塞采用的是CAX4R单元类型。

2) 模型的网格划分

密封圈的有限元模型由密封圈、活塞、缸壁3个部件组成，均采用二维轴对称模型 [13]，活塞与缸壁的间隙为0.1 mm，有限元装配模型如图5所示。

Figure 5. Assembly drawing

图5. 装配图

橡胶材料的密封圈在活塞运动的作用下会发生变形，需要对密封圈底部靠近缸壁间隙处进行网格细化，网格划分结果如图6所示。

Figure 6. Secondary sealring model meshing

图6. 副密封圈模型网格划分

副密封圈有限元模型的基本属性如表2所示。

Table 2. Basic properties of secondary seal ring

表2. 副密封圈基本属性

3) 边界条件及载荷的设置

在实际工程中，为表现油液流体的作用一般采用局部施力的方法 [14]，这一方法不能很好地体现出橡胶之间的相互作用。而这部分可通过Abaqus进行设置，其工作原理是通过设置初始点，将流体施加于其上，遇到接触面即发生相互作用，如图7所示。由于流体的流动受接触压力作用，当接触压力大于流体压力，油液流体将停止施加。这样就可以动态地找到零边界点，使结果更为准确、完善 [15] [16]。

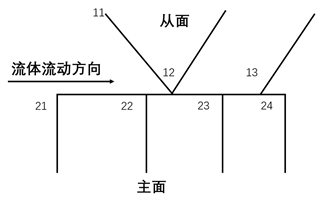
Figure 7. Diagram of fluid pressure osmotic loading

图7. 流体压力渗透加载原理图

分析步在仿真过程中设为两个，第一个分析步为1 s，是将密封圈移动与缸壁活塞接触，采用预调整的方法达到径向、轴向压缩，完成对密封圈的预压缩。第三个分析步为4 s，是对活塞施加一个向下的位移，同时给密封圈表面施加压强，模拟活塞运动的过程。使用上述流体的方式模拟流体压力，主从面分别选择密封圈和活塞、密封圈和缸壁。

边界条件是固定缸壁结构，将活塞施加轴向的往复位移运动。对活塞位移和制动主缸液压力的关系如下：

$d=2{\sigma }_{load}+2$ (11)

式中：d为活塞位移。

相互作用中共设置三个接触作用，密封圈分别和缸壁、活塞还有自身接触，接触应力方面设置为罚(Penalty)算法 [17]，其中摩擦系数为0.1。

3.2. 正交实验设计

密封圈的各类参数较为复杂，可考虑不同因素来进行优化。参考以往文献的大量研究，选取橡胶硬度、摩擦系数、活塞与缸体之间的距离、密封圈活塞位移四个参数进行研究，并在现有的条件下将每个参数取到四个水平。通过有限元软件Abaqus分别计算得到挤压点的最大Mises应力、挤压量和左密封处的磨损量。逐一进行仿真计算将会浪费大量的时间与成本，所以通过对拟合数据样本可以减少有限元仿真次数，这里使用正交试验可以计算不同工况等级别所对应的结果。本文使用L16 (45)正交表，采用的正交表及仿真结果如表3所示。

Table 3. Simulation result data

表3. 仿真结果数据

为进行方便优化后对比验证，计算得到密封圈原尺寸仿真结果，如下表4所示。

Table 4. Full scale simulation result data

表4. 原尺寸仿真结果数据

将表2和表3的结果数据整理到一起进行对比，如下图8所示。

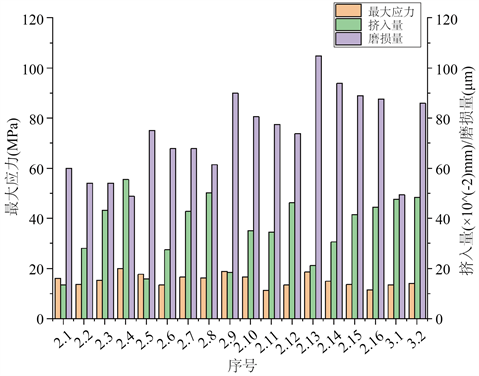
Figure 8. The bar graph of the simulation results

图8. 仿真结果的柱形图

4. 优化设计

4.1. 回归方程构建

本文选用的回归方程基本形式如下：

$y=a_0+{\displaystyle {\sum }_{i-1}^n{a}_i{x}_i}+{\displaystyle {\sum }_{i-1}^n{a}_{ii}{x}_i{}^2}+{\displaystyle {\sum }_{i\ge j}^n{a}_{ij}{x}_i{x}_j}$ (12)

式中：n为设计变量数目； $a_i$ 、 $a_j$ 和 $a_{ij}$ 为多项式系数。

最大Mises应力( $y_1$ )、挤入量( $y_2$ )、磨损量( $y_3$ )的回归方程表达式如下(保留小数点后4位数字)：

$\begin{array}{l}{y}_1=437.7822-1.4391x_1-10.6962x_2+725.4734x_3-352.0535x_4+0.0152x_1{x}_2-2.0799x_1{x}_3\\ +1.2104x_1{x}_4-7.95x_2{x}_3+4.1944x_2{x}_4+11.1111x_3{x}_4+0.0066x_1^2+0.0664x_2^2+160.2222x_3^2\end{array}$ (13)

$\begin{array}{l}{y}_2=-3.6581+0.0145x_1+0.1055x_2+3.435x_3+5.1816x_4-0.0003x_1{x}_2+0.0875x_1{x}_3-0.0502x_1{x}_4\\ -0.0485x_2{x}_3-0.0347x_2{x}_4+1.1667x_3{x}_4+0.0002x_1^2-0.0007x_2^2-0.7657x_3^2\end{array}$ (14)

$\begin{array}{l}{y}_3=854.8349-6.8863x_1-16.7698x_2-130.3354x_3-1603.1056x_4+0.0937x_1{x}_2-13.8568x_1{x}_3\\ +15.4397x_1{x}_4+5.4463x_2{x}_3+16.9833x_2{x}_4-2065.6667x_3{x}_4+0.0446x_1^2+0.0817x_2^2+936.3667x_3^2\end{array}$ (15)

回归方程的拟合是求出近似解，不同的系数选择将会导致方程精度的不同。因此，通过复相关系数这一标准来评价三个回归方程的精度。复相关系数越接近1，精度越好。回归方程 $y_1$ 、 $y_2$ 、 $y_3$ 的复相关系数分别为0.9995、0.9998和0.9991。所以，三个回归方程的拟合程度满足精度要求。

4.2. 帕累托(Pareto)最优解

多目标优化是没有唯一解的，通常会根据实际需要来有限地区选择一系列解，择优而取。其中，一个目标增加，与此同时另一目标减少，上述一系列解被称为帕累托最优解。因此，在获得帕累托最优解后，会根据项目的实际情况条件来抉择。

本文采用MATLAB相关遗传算法优化方法中的名为gamultiobj函数来优化，该函数是基于NSGA-II改进而来的一种多目标优化算法。本文以求得的3个回归方程为目标函数，以4个因素的水平最大与最小值为约束条件，求这3个目标函数同时较小时因素的数值。皮碗在基本工况下最大应力略微减少且集中在左下挤入处，与啃噬失效位置相同。为避免密封圈在实际工作中发生啃噬失效，需硬度越高、摩擦系数越大，对比原尺寸仿真结果对Pareto解集进行筛选，优选出的Pareto解集如表5所示。

Table 5. Optimized solution set

表5. 优化解集

对上述两个解进行验证，得到的结果如表6所示。

Table 6. Verification results

表6. 验证结果

为保证密封圈的防啃噬失效性能，且在电子制动助力器的实际工作环境中，摩擦系数多为0.1~0.15左右，经过比较考虑，选择1号解为最优解，当活塞位移为16 mm左右时，挤入量最小并能够尽量避免啃噬失效，且能够满足性能要求。相较于未优化之前，挤入量减少了1.01%，磨损量减少了0.78%，可以起到良好的优化效果。另外若是以优化磨损为目标并适当放宽摩擦系数范围，也选择2号解为最优解，虽然防啃噬方面性能减弱，但抵抗磨损的效果更好。

5. 结论

本章建立了主密封圈的有限元模型，通过正交试验设计、构建回归方程和遗传算法优化方法，对橡胶硬度、摩擦系数、活塞与缸壁间距、活塞位移等4个因素进行了优化选择。主要结论如下：

1) 通过大量Mises应力仿真以及对失效形式的分析，可以看出密封圈失效主要集中于其底部靠近间隙处，随活塞往复运动会逐渐产生各类疲劳破坏的问题。

2) 仿真结果显示橡胶的硬度应选择尽量较大的，密封圈会由于橡胶材料的硬度低，导致被挤进间隙。因此在设计密封圈需将硬度在有限范围内提高，以减少密封圈的啃噬和磨损量。

3) 通过多目标优化得到结构参数的最优组合，其中挤入量减少1.01%，在保证其它影响较小的情况下有效地防范啃噬现象；磨损量减少了0.78%，抗磨损性能也加强，具有良好的优化效果。