基于时间序列异常检测分析的方法

Method of Anomaly Detection and Analysis Based on Time Series

摘要: 不依赖于模型，基于累计变化量来实现异常点的检测，而无法检测出成片的异常点，并且很容易把正常点视为异常点，为了解决上述方法中所存在的问题，本文在所给方法的基础上重新定义了累计变化量，引入了推移算子，异常类型指示变量和异常惩罚量，并定义了两类异常类型，一种叫做高位异常，一种叫做低位异常，然后重新定义了异常点模型，引入了然后用2004年到2009年的沪市股票数据来进行数值实验，并对结果进行了对比证明了本文所给方法的有效性。

Abstract: About not dependent on the model and is relatively simple and easy to implement about the methods of the time series anomaly detection, but it can not detected a piece of outliers, and it is easy to make normal points as outliers. In order to solve the problems, on the basis of the method given, this paper redefines the cumulative change and introduces the transition operator, one indicator variable and unusual punishment are introduced in this paper and two exception types are defined, one is called the high anomaly, another is called the low abnormal. The effectiveness of the method given in this article is proved by using the data from Shanghai Stock Market between 2004 and 2009 be proved through numerical experiments. The results are compared to prove the effectiveness of the method presented in this paper.

1. 引言

在异常检测研究领域，经过了20多年的发展，已经产生了很多有效的方法，如统计学方法 [1] ，基于密度的方法，基于距离的方法。以上都是针对无序序列的异常点检测，由于时间序列的最重要一个特征就是具有时间属性，序列值之间必须按照时间先后顺序进行严格的排序，因此上面介绍的方法都不适合用于时间序列。目前针对时间序列中异常检测的方法主要有生物学方法 [2] ，机器学习的方法 [3] [4] ，基于小波的方法 [5] [6] ，基于AR模型的方法 [7] 等。虽然在对时间序列异常检测研究领域里已经产生很多种方法，但是这些方法还不是很成熟。并且目前对于时间序列异常点检测的方法大都需要在预先知道所给数据满足哪一种时间序列模型的基础上针对相应的模型来进行异常点检测，但是在一般情况下很难知道数据到底满足哪一种时间序列模型，而且，一些针对时间序列异常检测的方法很复杂不太容易实现，比如基于贝叶斯方法的异常检测，理论看起来很复杂，不仅需要抽样还要经过反复的迭代。

通过前面对时间序列异常检测的研究，结合文献 [8] 中的异常点检测方法给出了一种改进的模型，为了解决文献 [8] 中的模型不能检测出成片的异常点还有把正常点误以为是异常点的情况，在文中定义两种异常形式，一种叫做高位异常，一种叫做低位异常，并引入一个表示异常类型的示性变量和惩罚函数，最后借助计算机将模型应用于生活中实际数据。

2. 基础知识

定义1：设 $\left\{{\epsilon }_t\right\}$ 是 $WN\left(0,{\sigma }^2\right)$ ，且实系数多项式 $A\left(z\right)$ 和 $B\left(z\right)$ 没有公共根，满足以下所给的条件

$b_0=1,a_p{b}_q\ne 0$

$A\left(z\right)=1-{\displaystyle \underset{j=1}{\overset{p}{\sum }}{a}_j{z}^j}\ne 0,\left|z\right|\le 1$

$B\left(z\right)={\displaystyle \underset{j=0}{\overset{q}{\sum }}{b}_j{z}^j}\ne 0,\left|z\right|<1,$

那么我们就把下面的差分方程

$X_t={\displaystyle \underset{j=1}{\overset{p}{\sum }}{a}_j{X}_{t-j}}+{\displaystyle \underset{j=0}{\overset{q}{\sum }}{b}_j{\epsilon }_{t-j}},t\in Z$

称为自回归滑动平均模型，简称为 $\text{ARMA}\left(p,q\right)$ 模型。

定义2：给出一时间序列， $X=\left(x_1=\left(v_1,t_1\right),x_2=\left(v_2,t_2\right),\cdots ,x_n=\left(v_n,t_n\right)\right)$ 点 $x_{t_i}=\left(v_{t_i},t_i\right)$ 表示时间序列在 $t_i$ 时刻的观测值为 $v_{t_i}$ 。用 $\left(N_1,N_2,\cdots ,N_k\right)$ 表示点 $x_{t_i}$ 的k个邻居点集合，其观测值集合记为 $\left(v_{N_1},v_{N_2},\cdots ,v_{N_k}\right)$ ，给定阀值T，若点 $x_{t_i}$ 与其k个邻居点的累积变化量(Accumulative Change)大于T，则判定点 $x_{t_i}$ 为这段时间序列中的一个异常点，这一判定条件公式表示为

$\text{AccumulativeChange}=\frac{W_1\left|v_{t_i}-v_{N_1}\right|+W_2\left|v_{t_i}-v_{N_2}\right|+\cdots +W_k\left|v_{t_i}-v_{N_k}\right|}{W_1+W_2+\cdots +W_k}>T$

式中的 $\left(W_1,W_2,\cdots ,W_k\right)$ 为权值向量，赋予每个变化量不同的权重，一般来说，在时间轴上，越接近点 $x_{t_i}$ 的邻居点赋予的权值越大；阀值T是用户给定的一个常数量，点 $x_{t_i}$ 的累积变化量和阀值的大小关系，是判定 $x_{t_i}$ 是否为一个异常点的依据 [8] 。

3. 异常点模型建立

文献 [8] 中利用上面定义2判定的异常点模型是通过时间序列的波动来得到的异常点，因此不需要知道时间序列具体是符合什么样的模型，而且这种异常点模型也容易在现实应用中实现，但是也存在一定的缺陷：

1) 由于是通过时间序列的波动来实现异常点的检测，因此，在波动量不是很大但却很频繁的时候，累积变化量也可能很大。

2) 在异常点成片出现的时候，因为不知道异常点成片出现时的数目，因此T的选择对异常点的检测很重要，这个异常点模型往往识别不了成片的异常点，因为可能成片的异常点之间的变化不大，从而造成了它们间的累积变化量不是大。

文献 [8] 中的方法在经过了一片异常点后，往往会把第一个出现的正常值视为异常点，因为在成片异常点后面的正常数据相对异常点的变化很大，所以累积变化量也很大。因此本文所定义的异常点思想是居于文献 [8] 中累积变化量的思想，然后试图重新对异常点模型进行定义，从而解决文献中对异常点定义所存在的缺点。

在定义异常数据点模型前,先给出高位异常点和低位异常点的定义。

定义3如果一个异常点的数据比它相邻的数据大很多，则称这个异常点为高位异常点。

定义4如果一个异常点的数据比它相邻的数据小很多，则称这个异常点为低位异常点。

为了解决文献 [8] 中的问题，引入 ${\lambda }_i\left(i=1,2,\cdots ,k\right)$ ，称 ${\lambda }_i$ 为数据的异常类型和异常惩罚量C。其中 ${\lambda }_i$ 的取值如下：

1) 当某一数据点为高位异常点时，那么 ${\lambda }_i=1$ ；

2) 当某一数据点为低位异常点时，那么 ${\lambda }_i=-1$ ；

3) 当数据点为正常数据点时，那么 ${\lambda }_i=0$ 。

本文中重新定义累积变化量为：

$AC=\left|\frac{{\displaystyle {\sum }_i^k{W}_i}\left[\left(x_t-x_{t-i}\right)+{\lambda }_i\cdot C\right]}{W_1+W_2+\cdots +W_k}\right|$

然后引入推移算子B，则模型可写成：

$AC=\left|\frac{{{\displaystyle {\sum }_i^k{W}_i}}_i\left[x_t\left(1-B^i\right)+{\lambda }_i\cdot C\right]}{W_1+W_2+\cdots +W_k}\right|$

异常点模型为：

$AC=\left|\frac{{\displaystyle {\sum }_i^k{W}_i}\left[x_t\left(1-B^i\right)+{\lambda }_i\cdot C\right]}{W_1+W_2+\cdots +W_k}\right|>T$

C和T需要用户确定，当AC > T时，则认为 $x_t$ 数据点为异常点，为了知道异常点是偏大还是偏小，定义如下：当

$\frac{{\displaystyle {\sum }_i^k{W}_i}\left[x_t\left(1-B^i\right)+{\lambda }_i\cdot C\right]}{W_1+W_2+\cdots +W_k}>0$

则，异常点为高位异常点，并且该点的 ${\lambda }_i=1$ 。当

$\frac{{\displaystyle {\sum }_i^k{W}_i}\left[x_t\left(1-B^i\right)+{\lambda }_i\cdot C\right]}{W_1+W_2+\cdots +W_k}<0$

则，异常点为低位异常点，并且该点的 ${\lambda }_i=-1$ 。当

$\left|\frac{{\displaystyle {\sum }_i^k{W}_i}\left[x_t\left(1-B^i\right)+{\lambda }_i\cdot C\right]}{W_1+W_2+\cdots +W_k}\right|<T$

则，该点为正常数据点，并且该点的 ${\lambda }_i=0$ 。

4. 模型分析

本文中给出的模型相比较于文献 [8] 中的模型缺陷，有如下优势：

$\left|\frac{{\displaystyle {\sum }_i^k{W}_i}\left[x_t\left(1-B^i\right)+{\lambda }_i\cdot C\right]}{W_1+W_2+\cdots +W_k}\right|<T$

1) 因为文献 [8] 中的累积变化通过 ${\displaystyle {\sum }_i^k{W}_i}\left|v_t-v_{t-i}\right|$ 的值来表示的，因此，即使波动量不大，但是波动得很频繁的时候 ${\displaystyle {\sum }_i^k{W}_i}\left|v_t-v_{t-i}\right|$ 的值都会很大，而且，本文认为那些异常点莫非是相对于邻近点过大或者是过小的数据点，因此用 ${\displaystyle {\sum }_i^k{W}_i}\left(v_t-v_{t-i}\right)$ 来描述某一数据点对于邻近点的变化会更好一些。

2) 对于惩罚量的引入：因为文献 [8] 中的异常点模型是通过 ${\displaystyle {\sum }_i^k{W}_i}\left|v_t-v_{t-i}\right|$ 的值来确定的，因此在出现成片异常点的地方 ${\displaystyle {\sum }_i^k{W}_i}\left|v_t-v_{t-i}\right|$ 会很小，从而导致检测不出异常，本文引入的惩罚量就是当t时刻的数据点是异常点时它会对后续的数据产生影响，因此即使在出现成片异常点的情况下，当引入异常惩罚量之后，即使异常点之间真实的波动量并不大，但是本文定义的累积变化也会很大，这样就可以检测出成片的异常点。

3) 对于指示变量的引入，由于上面加入了异常惩罚量，但是如果每个异常所加的惩罚量都是正或是负的话也会出现问题，假设惩罚量全部都取为正数，那么，当遇到成片的异常点时并且这些异常点会比正常的数据点数值要低，则在成片异常点后面出现的正常点往往就会被认为是异常点，再假设惩罚量全部都取为负数，当遇到成片的异常点时并且这些异常点会比正常的数据点数值要高，则在成片异常点后面出现的正常点往往也会被认为是异常点，并且，引入具有三个取值的指示变量还有一个好处，就是不仅知道某个数据点是否异常而且还可以知道异常点是偏高了还是偏低了。

5. 数值试验

结合实际数据进行试验，所用的数据是2004年到2009年的沪市股票数据一共有302条数据。为了了解由于异常点的存在对时间序列数据建立模型的影响，下面将会对所给的数据在对异常点进行修正前后来进行拟合模型的对比，主要看所拟合的模型的参数在修正异常点前后的差异，因为一般的金融数据都会有异方差的，在这先对数据进行异方差的检验，然后用数据进行GRACH模型的检验。

首先对数据进行了异方差检验，异方差检验结果如图1显示：

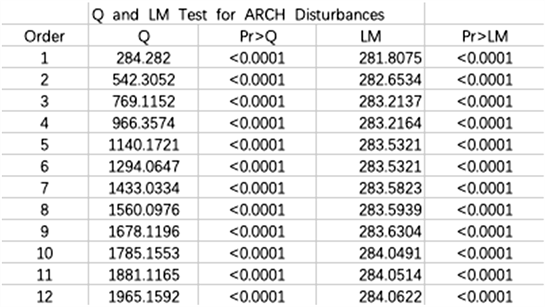
Figure 1. Heteroscedasticity test results

图1. 异方差检验结果

从上面图中可以看到，Q统计量从1到12的时滞窗体现出了方差随时间的变化，这些检验都显示数据存在着异方差。因此，用GRACH模型对数据进行建模，下面得到了GRACH模型的参数估计，如图2。

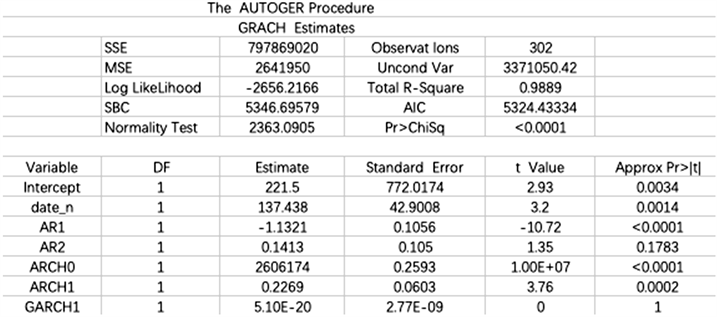
Figure 2. Parameter estimation of GRACH model

图2. GRACH模型的参数估计

用本文给出的异常检测方法对数据进行异常点的检测，然后与文献 [8] 中的方法进行对比。最后在异常点进行修正后对数据进行建模。我们的异常点判断模型为：

$AC=\left|\frac{{\displaystyle {\sum }_i^k{W}_i}\left[x_t\left(1-B^i\right)+{\lambda }_i\cdot C\right]}{W_1+W_2+\cdots +W_k}\right|>T$

异常修正后的参数估计结果如图3所示：

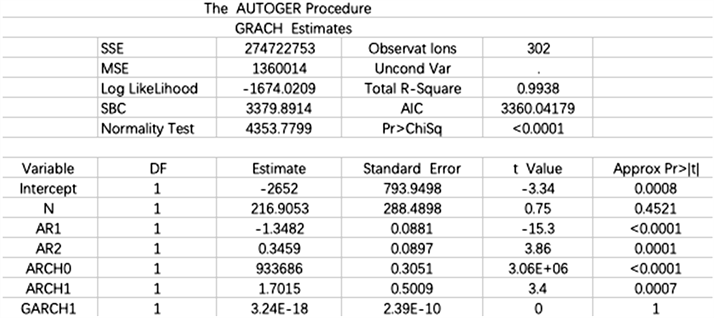
Figure 3. Parameter estimation after anomaly correction

图3. 异常修正后的参数估计

从图中可以看出，修正前与修正后的参数估计结果图相比，对异常点修正前后就行的建模，参数差别很大，因此，更加说明了异常检测的重要性。

6. 结语

在本文给出的异常点模型中引入了一个异常惩罚量，而且在数值试验时把它取值为滑动窗口数据的平均值，本文给出一个比较简单易于实施而且有效的异常点发现方法，该方法是基于文献 [8] 的基础，然后通过引入指示变量和惩罚函数，在最后的数值试验中也证明该方法的有效性。

参考文献