1. 引言
投射模是同调代数理论研究中非常重要的一种古典模类,上世纪九十年代,Enochs等 [1] 在任意结合环上引入Gorenstein投射模的概念,这是Auslander等引入的G-维数为0模的推广,也是经典同调代数中投射模在相对同调代数中的对应。此后,Gorenstein投射模受到了国内外学者的广泛关注。文献 [2] 中给出了(n, d)-投射模的定义,在此基础上我们对(n, d)-投射模进行了推广,给出了Gorenstein(n, d)-投射模的定义,并且对Gorenstein(n, d)-投射模进行了一般研究。
2. 预备知识
文中R和S均是有单位元的结合环,模均指酉模。我们用R-模(S-模)表示左R-模(左S-模),ROP-模(SOP-模)表示右R-模(右S-模)。设n,d都是非负整数。
表示ROP-模N的内射维数。
定义1.1 ROP-模U称为n-表现模 [3] ,如果存在ROP-模的正合列
,
其中每个
都是有限生成自由模
。
R是右n-凝聚环 [3] ,如果对任意n-表现ROP-模是(n + 1)-表现的。
ROP-模N称为(n, d)-内射模 [3] ,如果对任意n-表现ROP-模U,
。
ROP-模M称为(n, d)-投射模 [2] ,如果对任意(n, d)-内射ROP-模N,
。
注1.2 [4] 设R是环,m和n是整数,则以下成立:
1) 当
时,任意m-表现ROP-模是n-表现的。
2) 当
时,任意(n, d)-内射ROP-模是(m, d)-内射的。
3) 当
时,任意(m, d)-投射ROP-模是(n, d)-投射的。
3. Gorenstein(n, d)-投射模
定义2.1 称ROP-模G是Gorenstein(n, d)-投射模,如果存在(n, d)-投射ROP-模的正合列
,
使得
,并且对任意内射维数有限的(n, d)-内射ROP-模N,
正合。
定理2.2 设R是环,G是ROP-模。若R是一个右n-凝聚环,则G是Gorenstein(n, d)-投射模当且仅当存在(n, d)-投射ROP-模的正合列
,
使得
。
证明 必要性由定义显然成立。
设(n, d)-内射ROP-模N,且
,下证G是Gorenstein(n, d)-投射模。
考虑短正合列
,其中E是内射模。对m进行归纳,当
,显然
正合。
时,因为内射模是(n, d)-内射的,由文献 [2] 中引理3.4知(n, d)-内射模关于单同态的余核封闭,所以K是(n, d)-内射ROP-模。并且对任意
,
和
都是(n, d)-投射ROP-模。故
。得下面正合复形
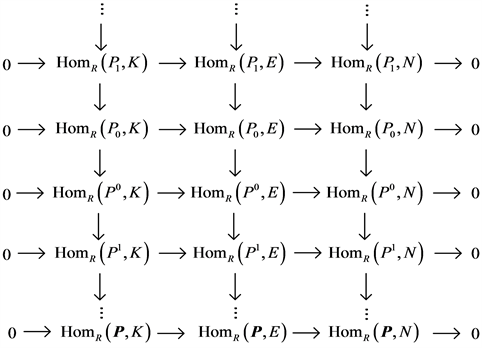
,由归纳假定知
正合。再由复形的长正合列定理,即
正合,得证。
推论2.3 设R是一个右n-凝聚环,G是ROP-模。则以下等价:
(1) G是Gorenstein(n, d)-投射模。
(2) 存在(n, d)-投射ROP-模正合列
。
(3) 存在ROP-模短正合列
,其中M是(n, d)-投射模,L是Gorenstein(n, d)-投射模。
证明 (1)
(2),(1)
(3)显然。
(2)
(1)对任意ROP-模G,存在正合序列
,其中
是投射模。因为投射模是(n, d)-投射的,连接这两个序列得到(n,d)-投射ROP-模正合序列
,使得
。由定理2.2可得G是Gorenstein(n, d)-投射模。
(3)
(2) 设ROP-模短正合列
,其中M是(n, d)-投射模,L是Gorenstein(n, d)-投射模,由(1)
(2),存在正合序列
,其中
是(n, d)-投射模,连接两序列得到正合序列
,即为所求。
命题2.4 设R是一个右n-凝聚环,G是ROP-模。若R是(n, d)环且G是Gorenstein(n, d)-投射模,则对任意整数
和任意内射维数有限的(n, d)-内射ROP-模N,
。
证明设G是Gorenstein(n, d)-投射ROP-模,则存在G的(n, d)-投射分解
,
将此序列打断

对任意(n, d)-内射ROP-模N,且
,以函子
作用短正合列仍正合,并且G,
都是Gorenstein(n, d)-投射ROP-模,所以
。在短正合列
中,由长正合序列引理得
,又R是(n, d)环,由文献 [2] 中定理4.4知(n, d)投射模是投射的,得
。在短正合列
中,由长正合序列引理得
,得
。由序列
,得
。依此类推,对任意整数
,故
。
我们用
表示ROP-模G的Gorenstein(n, d)-投射维数,
当且仅当G有长度为m的Gorenstein(n, d)-投射分解。
命题2.5 设R是一个右n-凝聚环,存在ROP-模短正合列
,若B是(n, d)投射模,则
。特别地,若G是Gorenstein(n, d)-投射ROP-模,则K也是。
证明 设
,则K存在长度为m的Gorenstein(n, d)-投射分解
。连接此序列和短正合列
,得G的Gorenstein(n, d)-投射分解
,故
。
特殊情况由推论1可得。
命题2.6 设R是一个右n-凝聚环,
是ROP-模短正合列。若A是Gorenstein(n, d)-投射模,H是(n, d)投射模,则G是Gorenstein(n, d)-投射的。
证明 若A是Gorenstein(n, d)-投射ROP-模,则存在ROP-模正合列
,其中,M是(n, d)投射模,L是Gorenstein(n, d)-投射的。
考虑下面的推出图

在行正合列
中,因为(n, d)投射模关于扩张封闭,所以D是(n, d)投射模。在列正合列
中,D是(n, d)投射模,L是Gorenstein(n, d)-投射模,由推论2.3,G是Gorenstein(n, d)-投射的。
命题2.7 设R是环,m和n是整数。则以下成立:
1) 当
时,任意Gorenstein(m, d)-投射ROP-模是Gorenstein(n, d)-投射的。
2) 若R是一个右n-凝聚环,当
时,任意Gorenstein(n, d)-投射ROP-模是Gorenstein(m, d)-投射的。
证明 1) 设G是Gorenstein(m, d)-投射ROP-模。当
时,任意(m, d)-投射ROP-模是(n, d)-投射的。则存在(n, d)-投射ROP-模正合列
,
又因为任意(n, d)-内射ROP-模是(m, d)-内射的,对任意内射维数有限的(n, d)-投射ROP-模N,
正合,故G是Gorenstein(n, d)-投射的。
2) 设G是Gorenstein(n, d)-投射ROP-模,R是一个右n-凝聚环。当
时,n表现ROP-模是m表现的,故(m, d)-内射ROP-模是(n, d)-内射的且(n, d)-投射ROP-模是(m, d)-投射的。则存在(m, d)-投射ROP-模正合列
,
对任意内射维数有限的(m, d)-投射ROP-模N,
正合,故G是Gorenstein(m, d)-投射的。
引理2.8 设
是一个环的满同态,
是投射ROP-模且
是投射R-模。若M是(n, d)-投射SOP-模,则
是一个(n, d)-投射ROP-模。
证明 设N是(n, d)-内射ROP-模,由文献 [4] 中引理4.1可得
是一个(n, d)-内射SOP-模。M是(n, d)-投射SOP-模,由文献 [5] 中推论10.65,则有同构
得
,故
是一个(n, d)-投射ROP-模。
引理2.9 设
是一个环的满同态,
是投射ROP-模且
是投射R-模。若M是(n, d)-投射ROP-模,则
是一个(n, d)-投射SOP-模。
证明 设N是(n, d)-内射SOP-模,则N是(n, d)-内射ROP-模。由文献 [5] 中推论10.65,则有同构
,
得
,故
是一个(n, d)-投射SOP-模。
命题2.10 设
是一个环的满同态,
是投射ROP-模且
是投射R-模。若N是一个ROP-模且
,则
。
证明 设任意SOP-模M,由文献 [5] 中推论10.65得同构式
.
若
,N是一个内射ROP-模,
时,上式右边等于零,故
,得
是一个内射SOP-模,即
。
若
,由上面同构式
,得
。
综上,
。
定理2.11设
是一个环的满同态,
是投射ROP-模且
是投射R-模,M是一个SOP-模。则以下价:
(1)
是Gorenstein(n, d)-投射ROP-模。
(2)
是Gorenstein(n, d)-投射SOP-模。
(3)
是Gorenstein(n, d)-投射SOP-模。
证明 (1)
(2)设N是(n, d)-内射SOP-模且
,由文献 [6] 中引理3.12知N是(n, d)-内射ROP-模且
。再由文献 [4] 中引理4.1得
是(n, d)-内射SOP-模,故
也是(n, d)-内射ROP-模。由命题2.10得
,同时
。由(1)
是Gorenstein(n, d)-投射ROP-模,存在(n, d)-投射ROP-模的正合列
,
其中,
。即存在(n, d)-投射SOP-模的正合列
,
其中,
。由伴随同构
.
对任意内射维数有限的(n, d)-内射ROP-模
,因为f满,由文献 [5] 命题8.33,所以
。由条件(1),
正合,故对任意(n, d)-内射SOP-模N且
,
正合,得
是Gorenstein(n, d)-投射SOP-模。
(2)
(3)由
,故
是Gorenstein(n, d)-投射SOP-模。
(3)
(1)设P是(n, d)-投射SOP-模,则P是(n, d)-投射ROP-模。
是Gorenstein(n, d)-投射SOP-模,则存在(n, d)-投射ROP-模的正合列
,
其中,
。设N是(n, d)-内射ROP-模且
。由文献 [4] 引理4.1和命题2.10得
是一个(n, d)-内射SOP-模且
。由同构
,
由条件(3),对任意内射维数有限的(n, d)-内射SOP-模
,
正合,故对任意(n, d)-内射ROP-模N且
,
正合,得
是Gorenstein(n, d)-投射ROP-模。