1. 引言
实腹梁–柱连接在低周往复荷载作用下，柱翼缘与梁翼缘之间焊缝易发生开裂，严重影响塑性变形充分发展并导致滞回性能劣化。目前解决连接节点发生脆性破坏的设计方法之一为梁腹板削弱型节点 [1] [2] [3] ，该类节点与实腹梁式节点相比，可以减缓节点域应力集中程度，避免节点连接处焊缝先于梁截面发生破坏，使塑性铰形成在远离梁柱连接处的梁截面，从而保护节点域。此外，采用腹板开孔梁便于建筑设备管线的穿越，有节省空间、降低层高、减少用钢量等优点。目前国内外在蜂窝梁钢框架结构抗震性能方面取得了较多的研究成果 [4] [5] [6] [7] ，而蜂窝梁钢框架十字型连接节点的受力性能研究特别是抗震性能方面的研究还不多见，对于其孔洞参数的合理取值范围等，更是缺乏大量系统化的研究，使得蜂窝式钢框架结构在我国的应用范围受到了制约。因此本文对蜂窝梁钢框架十字型节点的抗震性能展开研究。
本文选取蜂窝梁钢框架结构中的十字型节点为研究对象，依据沈阳建筑大学蜂窝梁与蜂窝组合梁柱节点抗震性能试验 [8] ，建立有限元模型，采用理论分析与数值模拟相结合的方法和手段，分析蜂窝梁钢框架十字型连接节点的抗震性能，探讨开孔率和首孔距离柱边距离对抗震性能的影响，为蜂窝梁钢框架十字型节点的设计和工程应用提供参考。
2. 有限元模型建立及验证
2.1. 有限元构件尺寸
本文通过ABAQUS有限元程序根据试验建立有限元计算模型。图1为沈阳建筑大学蜂窝梁与蜂窝组
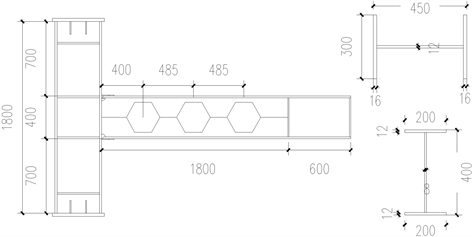
Figure 1. Specimen size diagram of FWLZ-1
图1. FWLZ-1试件尺寸示意图
合梁柱节点抗震性能试验中构件编号为FWLZ-1的节点模型，构件详细尺寸为：梁截面尺寸H400 × 200 × 8 × 12 (mm)，柱截面尺寸为H450 × 300 × 12 × 16 (mm)。蜂窝梁上采用六边形开孔。
2.2. 钢材本构关系
钢材采用双折线本构模型，包括弹性阶段和塑性阶段。本文材料选用Q355B钢材，材料性能如表1所示，梁长度为2100 mm，柱高1800，全焊缝连接。
2.3. 单元选取与网格划分
有限元建模中，所有钢材采用空间三维缩减积分实体单元(C3D8R)，便于在接触分析中，保证计算精度。在有限元模拟分析中，网格划分精细程度的大小对结果的影响较大，网格过大会导致计算结果与实际结果相差较大，而网格过小会使得模型计算耗时且导致模型计算不收敛，因此在经过多次试算对比后，网格尺寸确定为：H形钢柱网格尺寸为50 mm，蜂窝钢梁网格尺寸40 mm，节点局部进行网格加密处理。
2.4. 相互作用及边界条件
本有限元模型包括钢梁、柱，有限元标准模型图如图1所示。在梁端施加低周反复荷载。钢梁与H形钢柱之间采用绑定(tie)连接到一起。
试验试件为柱顶和柱底刚接，要求模型边界条件与实际试验边界条件相同，但因为轴压比的原因需要在柱顶施加荷载，因此柱顶的纵向位移不固定，而柱底固定。
2.5. 加载方案
试件采用先向柱顶竖向加载(轴压比0.25)，且在整个过程中保持恒定不变，再通过MTS电液伺服系
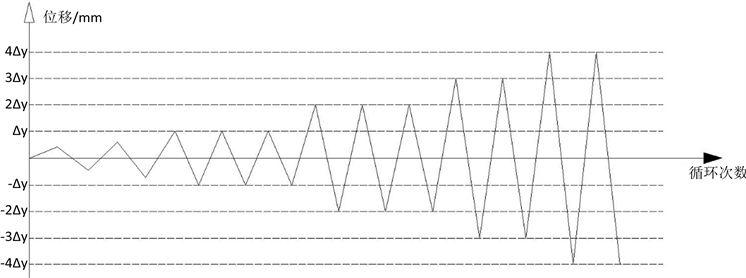
Figure 2. Schematic diagram of loading scheme
图2. 加载方案示意图
统对梁端施加低周反复循环荷载，如图2所示，所有构件均采用相同的加载方式和边界约束条件，以便控制变量做比较，并且使模拟条件和试验条件基本一致。梁端循环荷载采用位移控制加载；屈服前，每级循环一次。屈服后采用位移控制的方式加载，3Δ前每级循环三周，3Δ后每级循环两周直至构件破坏或荷载下降到极限荷载的85%终止试验。
3. 试验结果与有限元结果对比
3.1. 破坏形态比较
如图4所示，在循环往复加载的过程中，梁柱连接处应力相对较小，蜂窝钢梁首孔处出现梁翼缘屈曲，节点破坏发生在首孔处，较好的实现了塑性铰的外移，达到了强柱弱梁的设计目标。
3.2. 滞回性能比较
图3为模拟的滞回曲线与原试验测得的滞回曲线对比情况，从图中可以看出，两者滞回曲线走势及
(a) 
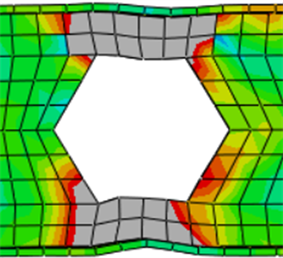(b)
Figure 3. Comparison of test failure diagram and finite element; (a) FWLZ60-400 cellular beam failure diagram; (b) FWLZ60-400 honeycomb beam simulation damage diagram
图3. 试验破坏图与有限元对比；(a) FWLZ60-400蜂窝梁破坏图；(b) FWLZ60-400蜂窝梁模拟破坏图
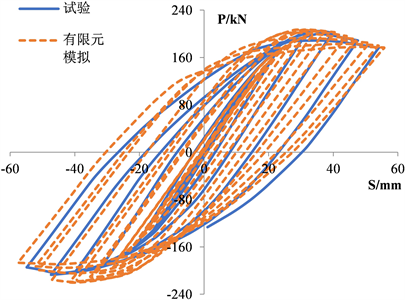
Figure 4. Comparison of the test and finite element
图4. 试验与有限元对比
形态较吻合，滞回环面积较大能够吸收一定的能量，表明蜂窝梁与H形钢柱的刚性连接节点具有较好的抗震性能。由于有限元模拟过程均比实际试验更具理想化，本有限元模型并没有考虑焊缝和钢材的初始缺陷，使得有限元模拟的滞回曲线更为饱满。从图4中可以看出试件试验结果与有限元模拟结果吻合度较高。
3.3. 承载力比较
从表2可以看出，试验值与有限元模拟值相差不大，误差控制在1.3%以内，说明有限元模拟与试验拟合度较高，可采用模拟对其进行进一步研究分析。
Table 2. Comparison of ultimate bearing capacity test values and finite element simulation values
表2. 极限承载力试验值与有限元模拟值比较
综合以上对有限元模型与试验对比可知，此有限元模拟与试验拟合度较高。由此可见，采用这种方法模拟蜂窝梁钢框架十字型连接节点具有很高的精度，可用来对其进行进一步的研究。
4. 考虑开孔率和开孔位置对十字型节点抗震性能的影响
在已有研究中可知，腹板开孔对于蜂窝梁的抗震性能影响较大，发现在一定范围内变化的开孔率和在一定范围内变化的开孔距离对蜂窝梁的抗震性能影响较小，为了使开孔率和开孔距离对于蜂窝梁抗震性能的影响规律更具有普遍性，根据开孔率和开孔距离的不同，建立更多的蜂窝梁十字型连接节点，并研究其抗震性能的变化规律。
根据表3所示节点尺寸参数，以图1中的FWLZ60-1为构件基本尺寸，在实腹柱另一侧增加与图1蜂窝梁尺寸相同的梁，使之成为图5所示的十字型节点，通过ABAQUS软件建立以下尺寸有限元模型 [9] [10] ，图5为FWLZ60-400的六边形孔蜂窝梁钢框架十字型连接节点，其中FWLZ表示蜂窝梁柱连接，60表示开孔率为60%，400表示开孔位置距离梁端为400 mm [10] 。
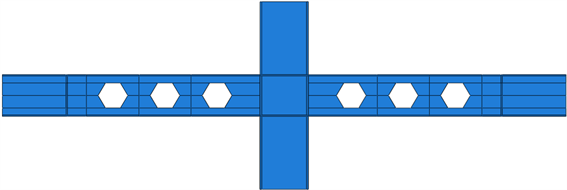
Figure 5. Comparison of the test and finite element
图5. 试验与有限元对比
Table 3. Size parameters of cross-type nodes
表3. 十字型节点尺寸参数
4.1. 滞回曲线
图6为九个试件的滞回曲线，通过观察滞回曲线的饱满程度来衡量3蜂窝梁–实腹柱十字型节点抗震性能的好坏，是抗震性能评价的重要指标。
蜂窝梁–实腹柱十字型节点因梁上蜂窝孔洞的存在，导致截面削弱，在一定程度上影响了滞回曲线的饱满程度。比较各节点模型的滞回曲线，开孔率为60%，首孔距离为1倍梁高时，滞回环面积相对较大，滞回性能较好，开孔率为50%；首孔距离为1倍梁高时，滞回环包围面积略小于上述试件；开孔率为70%，首孔距离为0.5倍梁高时，滞回环面积明显小于其他试件，耗能能力相对较差。
4.2. 骨架曲线
通过提取以上各试件滞回曲线的峰值点，所围成的曲线为试件的骨架曲线，各蜂窝梁–实腹柱十字
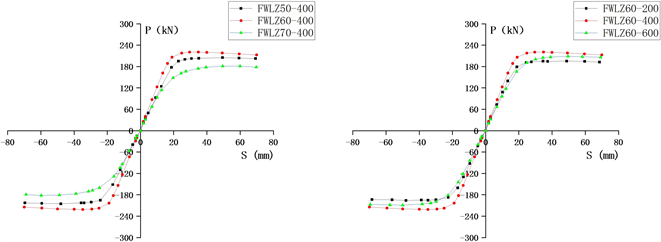(a) 60%开孔率节点模型骨架曲线图 (b) 首孔距离为400节点模型骨架曲线图
Figure 7. Skeleton curve
图7. 骨架曲线
Table 4. Load and displacement values for each model
表4. 各模型荷载与位移值
型节点的骨架曲线如图7所示。根据骨架曲线计算各试件屈服位移、屈服荷载、极限荷载和极限位移。
通过观察图7和表4可知，随着蜂窝开孔率越大，塑性铰外移现象越加明显，当蜂窝梁开孔率为60%，开孔距离为一倍梁高，即400 mm时，塑性铰位于蜂窝孔处，然而当开孔率继续增加时，屈服荷载也随即减小，说明由于腹板削弱过多，承担剪力和弯矩的作用相对减少，承载能力下降明显。而开孔位置的影响则不同，距离梁端过近或者过远都会使得蜂窝梁–实腹柱十字型节点的屈服荷载降低，而在一倍梁高时承载力最好，既可以使得破坏为延性破坏，又不会明显影响承载力。
4.3. 延性
本文采用延性系数μ的计算公式如下：
(1)
式中，u为延性系数；uu为骨架曲线中峰值荷载的85%所对应位移；uy为结构的屈服位移。
结构的屈服位移、极限位移和延性系数如表5所示。经比较，其中开孔率为60%，首孔距离为400 mm，即编号为FWLZ60-400的蜂窝梁–实腹柱十字型节点的延性系数值为所有模型的最大值为3.12，开孔率为70%，首孔距离为600 mm，即编号为FWLZ70-600的蜂窝梁–实腹柱十字型节点的延性系数值为所有模型的最小值为1.24。
4.4. 耗能能力
等效粘滞阻尼系数
计算方法如下所示：
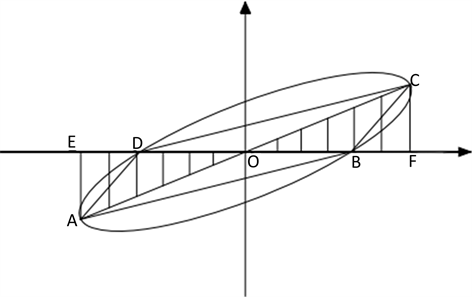
Figure 8. Schematic diagram of equivalent viscous damping coefficient
图8. 等效粘滞阻尼系数示意图
(2)
如图8所示，SABCD为试件循环一周所耗散的能量，SOEA和SOFC为试件所吸收能量的大小。能量耗散系数E为试件在一个滞回环的能量总值同试件弹性能的比值，定义为：
(3)
根据公式所得各蜂窝梁–实腹柱十字型节点峰值荷载滞回环的等效粘滞阻尼系数
和能量耗散系数E如表6所示。对比各试件的等效粘滞阻尼系数和能量耗散系数，
1) 随着开孔率的增大，蜂窝梁的延性系数和能量耗散系数均有所减小，说明钢梁腹板被削弱程度越大，对蜂窝梁–实腹柱十字型节点的抗震性能越不利；
2) 当首孔距离为一倍梁高时，试件的耗能能力明显优于其他试件，结构的耗能能力最好。当首孔距离梁端较近或较远时，试件的耗能能力都会下降。
Table 6. Peak load energy dissipation coefficient
表6. 峰值荷载能量耗散系数
5. 结论
1) 合理地利用蜂窝开孔的削弱作用可以将焊缝处的应力最大点转移到第一个蜂窝开孔处，使塑性铰由节点域向第一个孔洞处转移，避免在节点域破坏，提高了蜂窝梁–实腹柱十字型节点的延性，防止结构发生脆性破坏。
2) 随着开孔率的增大，塑性铰外移现象越明显，蜂窝梁–实腹柱十字型节点的承载能力增大，但是当开孔率超过一定比例时节点的承载能力有所下降，梁上蜂窝孔洞对蜂窝梁–实腹柱十字型节点的承载力削弱作用较大，对抗震性能产生了不利的影响，建议取值为60%时，蜂窝梁–实腹柱十字型节点承载能力最好。
3) 与开孔率的影响规律类似，开孔位置过大或过小均会降低蜂窝梁–实腹柱十字型节点的承载力，并影响延性、耗能能力等抗震性能指标，建议取值为一倍梁高时，蜂窝梁–实腹柱十字型节点抗震性能最好，且延性最佳，既可以起到塑性铰外移，保持延性破坏，又不至于严重影响承载能力。