1. 引言
气动技术具有响应快、廉价、可靠、易保养等优点 [1] ,大量应用于工业生产中。例如在特定的气压环境下对某些物品进行保存,或者是在特定的气压环境下对某些产品的性能进行检测等 [2] [3] 。在仪器仪表行业,为提高气动仪表的检测精度,要求对气压的控制快速、精准、稳定 [4] ;同时为测试比较不同材料之间的性能差异,需系统能控制多个管路的气压输出,这要求系统对总管的气压及最多64支路的气压控制精准。然而由于空气的可压缩性、控制阀的非线性流量特性以及非线性摩擦力特性等因素的影响,气压控制系统是一个强非线性系统 [5] ,同时64支路气压系统中的各支路气压的变化不仅会影响其他支路气压的变化,还会影响总管气压的变化,导致各支管气箱中的气压与总管的气压产生了耦合震荡,这给气压的精准控制增加了困难。
文献 [6] 针对电子比例阀的控制,提出了一种自适应控制算法,该方法对工作条件大范围变化时,能够准确的辨识出相应PID参数进行准确控制,但该方法在接近目标气压值时,上升时间较长。文献 [7] 针对液压缸的控制设计了一种BP神经学习算法——梯度下降法,但此算法全局寻优能力不佳,容易陷入局部极值。文献 [8] 针对气箱压力控制,提出了一种IPSO-BP-PID控制算法,通过用粒子群算法优化BP神经网络的加权系数得到最优权值,并按BP神经网络学习训练测试,得到最佳的PID控制参数,该方法只停留在仿真阶段并未得到实际运用。文献 [9] 针对容腔气压的控制,提出了一种模糊PID的控制算法,解决了气压控制非线性造成PID参数难以整定的问题,但在接近目标气压时过度过程时间长,未能克服高速开关电磁阀小信号死区时间特性带来的问题。
因此,在前人研究的基础上,本文针对气压控制系统的强非线性以及支管与总管之间的耦合特性,使用AMESim与Matlab软件的系统建模及仿真分析等功能,搭建了一套气压控制系统仿真模型,对其气压控制系统的性能展开研究。本文提出了一种自适应积分补偿神经网络模糊控制算法,是由自适应积分控制器与自适应神经网络模糊推理系统(ANFIS)相结合而来。实验结果表明该方法不仅抑制了支管与总管之间的耦合震荡,还实现气压的快速稳定跟踪控制效果,具有良好的控制性能,优于传统的PID控制与模糊控制。
2. 系统的数学模型
2.1. 高速开关电磁阀模型
气动高速开关电磁阀的组成通常包括机械、电磁和气体传动三个部分 [10] ,如图1所示。其工作原理为:当励磁线圈上电,电磁力与阀芯右侧气体压力共同克服弹簧力让阀芯左移,供气口P和作用口A导通,气体就会经过A口和P口进入到系统中去,实现加压操作;当励磁线圈断电,复位弹簧力克服阀芯右侧气体压力使得阀芯右移,排气口R和作用口A导通,气体就会经过A口和R口排入大气中,实现卸压操作。
 1. 扼铁;2. 静铁芯;3. 复位弹簧;4. 励磁线圈;5. 动铁芯;6. 隔磁环;7. 连接杆;8. 阀体;9. 阀芯
1. 扼铁;2. 静铁芯;3. 复位弹簧;4. 励磁线圈;5. 动铁芯;6. 隔磁环;7. 连接杆;8. 阀体;9. 阀芯
Figure 1. Structure diagram of high-speed switch solenoid valve
图1. 高速开关电磁阀结构简图
高速开关电磁阀的流量模型通常采用理想气体流过阀口的质量流量方程 [11] 表示如下:
(1)
式中:
——气体质量流量,kg/s
——阀口流量系数
——阀口节流面积,m2
——分别为阀口前后的气体压力,Pa
T——气体温度,K
——空气的比热容比
R——理想气体常数,J/(kg∙K)‒1
——临界压力比。
2.2. 气缸模型
假设气缸腔内气体状态变化过程为绝热过程,同时气体温度在充放气过程中保持不变且等于环境温度 [12] 。根据理想气体状态方程、质量连续性方程建立气缸腔内的压力微分方程如式(2)所示:
(2)
式中:
—气缸腔内气体的压力,Pa
—体积,
—腔内的净质量流量,
。
根据牛顿第二定律,气缸活塞的动力学方程为:
(3)
式中:
—气缸输出杆与负载的总质量,kg
,
—有效作用面积,m2;无杆腔气压,Pa
,
—有效作用面积,m2;有杆腔气压,Pa
—气缸运动过程中的摩擦力,N
—大气作用在气缸输出杆端产生的力,N。
2.3. 气压系统模型搭建
在上述分析高速开关电磁阀和气缸工作原理的基础上,使用AMESim软件的机械库、信号库、控制系统库和气动库中选择合适的元件,搭建高速开关电磁阀、气缸、负载以及电控部分等模型,将以上建立的高速开关电磁阀、气缸以及电控部分三大系统仿真模型按照一定的逻辑关系连接起来,然后再添加整个系统的压力源元件和传动元件,最后便可组成完整的气压控制系统AMESim仿真模型,如图2所示。系统模型的主要参数如表1所示。

Table 1. System model parameter setting
表1. 系统模型参数设置
3. 自适应积分补偿神经网络模糊控制
本文提出的自适应积分补偿神经网络模糊控制器由自适应神经网络模糊推理系统(ANFIS)与自适应积分控制器两部分组成。
3.1. 自适应神经模糊推理系统(ANFIS)
自适应神经模糊推理系统(ANFIS)模型由Jang在1993年首次提出 [13] 。它可以被认为是一个具有神经网络学习能力的Sugeno-type模糊系统。该网络由不同层级的具有特殊功能的节点组成。图3是ANFIS
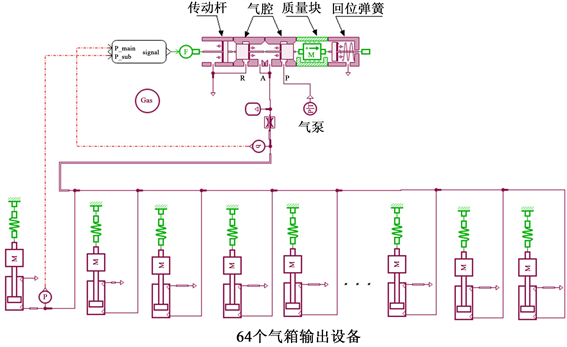
Figure 2. Simulation model of air pressure control system
图2. 气压控制系统仿真模型
网络的典型结构图。在第1层,每个节点是一个具有节点函数的自适应节点,其函数可以采用三角形隶属函数或高斯隶属函数。在第2层,每个节点都是一个固定节点,它代表每个规则的激励强度,同时它的输出是所有输入信号乘积。在第3层,每个节点也都是一个固定的节点,第i个节点计算第j条规则的激励强度与所有规则的激励强度之和的比值。在第4层,每个节点是一个拥有节点函数的自适应节点,它表示第i个规则对整体的贡献输出。在第5层,此单节点是固定节点,它是所有传入信号的整体输出求和 [14] 。自适应神经网络模糊推理系统将自适应神经网络与模糊推理联结到一起,对气压控制系统中的输入、输出数据进行学习和训练,从而构建神经网络结构,并建立推理模型、隶属度函数与模糊规则表,对实际的气压变化进行预测控制,从而实现气压快速跟踪控制。
3.2. 自适应积分控制器
由于高速开关电磁阀存在小信号死区时间的特性,且不同电磁阀之间的死区时间也有一定的差异。在ANFIS系统模型中引入了一个自整定积分控制器,以消除实验产生的稳态误差,达到气压快速精准的跟踪控制性能。本文使用的自适应积分控制器算法如下:
1) if
then
2) if
and
then
3) if
then
其中,u为积分因子输出量,e为当前目标气压与实时气压的差值,
为气压误差阈值,作为一个界限能够细化较小的偏差进而提高系统控制精度。k、
为积分控制算法的累计计算因子,他们的值需要根据实际工况中的条件来选取和调整。
4. 仿真结果及分析
基于MATLAB/Simulink平台搭建的自适应积分补偿神经网络模糊控制系统仿真模型如图4所示。通过搭建相应的自适应神经网络对模糊规则进行训练和学习,在推理算法中对整个气压控制回路中收集到的训练数据集进行仿真训练,得出一个自适应神经网络模糊控制规则以及相应的隶属度函数。同时系统中还包含一个自适应积分控制器,通过对实时采集到的误差进行调节相应的积分输出。将ANFIS控制器的输出与自整定积分控制器的输出共同作用于控制高速开关电磁阀,实现气压跟踪控制。图4中的被控对象为在AMESim软件中搭建的高速开关电磁阀以及气箱等组成的系统模型,通过在AMESim与Simulink中创建相应的接口模块,从而实现AMESim与Simulink的联合仿真。
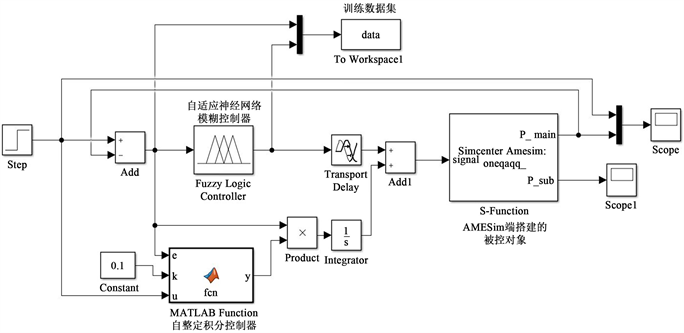
Figure 4. Joint simulation system model in Simulink toolbox
图4. 在Simulink工具箱中的联合仿真系统模型
通过设定目标气压为4 bar,利用Simulink和AMESim进行联合仿真,采用传统PID控制、自整定积分补偿模糊控制方法与改进的自适应神经网络模糊控制方法控制气压的输出,得到了三种不同控制方法的气压输出曲线。
4.1. 传统PID控制仿真结果
在采用传统PID控制时,系统中的总管和各支管气压变化如图5所示。从图中气压变化曲线可以看出此时气压的上升时间为2~3秒,超调量为0.6 bar左右,但总管与支管气压产生了强烈的震荡,这是由于各支路气箱中的气压与总管的气压产生了耦合震荡,各支路气压的变化不仅会影响其他支路气压的变化,还会影响总管气压的变化,导致总管中的气压耦合震荡效果加剧。
 (a)
(a)  (b)
(b)
Figure 5. Air pressure change under traditional PID control. (a) Pressure change in header; (b) Pressure change in branch pipe
图5. 传统PID控制气压变化。(a) 总管中的压力变化;(b) 支管中的压力变化
4.2. 自适应积分补偿模糊控制仿真结果
在采用自适应积分补偿模糊控制时,系统中的总管和各支管气压变化如图6所示。该控制算法是将本文设计的自适应积分控制器与传统模糊控制相结合共同控制系统气压。从图中气压变化曲线可以看出此时气压的上升时间为1~2秒,超调量为0.4 bar左右,且总管和支管之间的震荡效果相较于传统PID控制有所减弱,且在6秒后气压达到稳定。说明本文提出的自适应积分补偿模糊控制算法对系统总管与支管之间的耦合震荡有一定的减弱效果,但气压的控制在初期仍然会存在一定程度的震荡并且存在超调的情况。
 (a)
(a)  (b)
(b)
Figure 6. Adaptive integral compensation fuzzy control pressure change
图6. 自适应积分补偿模糊控制气压变化
4.3. 自适应积分补偿神经网络模糊控制仿真结果
在采用自适应积分补偿神经网络模糊控制时,系统中的总管和各支管气压变化如图7所示。从图中气压变化曲线可以看出此时气压的上升时间为0.8秒,超调量几乎为0,并且消除了总管与支管之间的耦合震荡,系统稳定性提升显著。经过实验得到的数据训练出的自适应积分补偿模糊控制模型能够有效的减缓气压系统中总管与支管之间耦合震荡。由此可见,本文提出的自适应积分补偿ANFIS算法在气压控制上超调量小、响应快、无震荡、系统平稳性好,对系统性能提升显著。
 (a)
(a)  (b)
(b)
Figure 7. Adaptive integral compensation neural network fuzzy control of pressure change. (a) Pressure change in header; (b) Pressure change in branch pipe
图7. 自适应积分补偿神经网络模糊控制气压变化。(a) 总管中的压力变化;(b) 支管中的压力变化
5. 总结
本文设计的气压控制系统从智能控制的角度出发,使用AMESim软件的系统建模及仿真分析等功能,搭建了一套64路的气压控制系统仿真模型,并通过软件提供的接口实现了与Matlab/Simulink的联合仿真,对其气压控制系统的性能展开研究。之后分别设计了自适应积分补偿模糊控制算法与自适应积分补偿ANFIS算法实现气压的解耦控制。经过实验测试,自适应积分补偿ANFIS算法相较于传统PID的控制算法能够抑制其强烈的耦合震荡,并且上升时间仅为0.8秒,气压在达到目标值后总管与支管并无明显震荡,同时能够很好的解决电磁阀非线性及存在小信号量死区时间的特性。表明了采用自适应积分补偿ANFIS算法的系统具备超调量小、响应快、无震荡、鲁棒性好等特点。因此自适应积分补偿ANFIS算法对非线性、迟滞等复杂的控制对象可迅速响应系统变化,可满足系统控制要求,在气压稳定控制上具有一定的借鉴意义。
NOTES
*第一作者。
#通讯作者。