植入NiTi-玄武岩混编纤维增强体的复合材料螺旋弹簧刚度预测模型

Stiffness Prediction Model of Composite Hel-ical Spring Embedded with NiTi-Basalt Hy-brid Braided Fiber Reinforcement

摘要: 为了预测植入NiTi-玄武岩纤维混编纤维增强体的复合材料螺旋弹簧刚度，基于复合材料细观力学推导了混编织物复合材料单层板的等效剪切模量计算公式，建立了多层异种纤维混编织物增强复合材料螺旋弹簧的刚度预测模型。制作了多层NiTi丝和玄武岩纤维混编复合材料螺旋弹簧样件。试验刚度与理论计算刚度误差为2.7%，验证了提出的刚度预测模型的正确性，这对异种纤维增强复合材料结构刚度性能预测及工程化应用具有参考意义。

Abstract: In order to predict the stiffness of composite helical spring embedded with NiTi-basalt hybrid braided fiber reinforcement, the equivalent shear modulus calculation formula of orthogonal hy-brid braided composite plate was derived based on composite micromechanics, and the stiffness prediction model of composite helical spring reinforced by multi-layer dissimilar fiber hybrid braided was established. In addition, the multi-layer NiTi wire and basalt fiber hybrid braided composite helical spring specimen was made. The error between the experimental stiffness and the theoretical calculation stiffness is 2.7%, which verifies the correctness of the proposed stiffness prediction model. This work has reference significance for the stiffness performance prediction and engineering application of dissimilar fiber reinforced composite structures.

1. 引言

为顺应汽车发展轻量化、智能化以及环保趋势，将具有形状记忆特性的NiTi丝和具有环保特性的玄武岩纤维混编织物应用于螺旋弹簧，在温度激励下可以实现变刚度驱动。螺旋弹簧的主动变刚度特性对提高汽车悬架的动力学性能具有重要意义 [1] [2] 。刚度预测模型是植入NiTi-玄武岩混编纤维增强体的复合材料螺旋弹簧实现工程应用需要解决的首要问题。

目前对于复合材料螺旋弹簧的刚度预测，从宏观力学角度分析，M. GOBBI [3] 、陈潇凯 [4] 等人通过分析簧丝截面的应力–应变关系，建立了复合材料螺旋弹簧刚度预测数学模型。Ke [5] 等人用相同方法扩展建立了具有非线性刚度的复合材料螺旋弹簧刚度理论模型。该理论方法能够解决多层材料构成的弹簧刚度计算问题，但公式较为复杂，在实际设计使用中颇为不便。从细观力学角度分析，Choi [6] 等人提出用等效剪切模量计算复合材料螺旋弹簧刚度，并通过圆形梁扭转实验验证了等效剪切模量计算模型的正确性。随后，相关学者 [7] [8] [9] 通过实验和仿真验证了弹簧刚度预测模型的正确性。在设计使用过程中，等效剪切模量预测弹簧刚度的计算方式简单，但目前还局限在使用单一增强纤维单层板的阶段。对于多层含有不同材料组分的织物复合材料单层板组合而成的层合板，现有的刚度预测模型均不适用。多种纤维混杂是丰富性能设计的重要手段，可以弥补单一纤维的性能缺陷 [10] [11] 。徐欢欢 [12] 和喻雄 [13] 通过宏观力学分析得出混编复合材料的柔度矩阵与工程常数之间的关系。在实际使用，特别是在工程设计中，柔度矩阵的计算相对复杂，用基于混合定则的公式计算会更方便。田毅 [14] 使用混合定则计算了单向混杂复合材料纵向弹性模量。陈庆林 [15] 对混杂纤维复合材料弹性模量预测模型进行了修正。但目前还没有一套完整混编正交织物复合材料工程弹性常数的计算公式。

本文建立了一种通用的多层异种纤维混编织物增强复合材料螺旋弹簧刚度预测模型。相较于现有的需要求解刚度或柔度矩阵的复合材料弹簧刚度计算模型，本文建立的工程常数计算公式更简便，更适用于工程设计，并且计算所得的工程常数方便用于有限元仿真模型。对于簧丝每一编织层的等效剪切模量，基于细观力学，建立了层内异种纤维混合正交编织的复合材料工程弹性常数计算模型。为了验证所建立预测模型的正确性，通过NiTi丝和玄武岩纤维混合编织，并采用真空辅助树脂传递工艺将弹簧样件制作成型。在万能试验机上对弹簧进行压缩试验，测得弹簧刚度与理论预测结果基本吻合，验证了预测模型的正确性。

2. 模型建立及刚度预测

本文在建立刚度理论预测模型时，选择理论通用性强的空心螺旋弹簧。若中间芯材使用的材料模量相较于外层复合材料小很多，对弹簧刚度贡献较小，可以视为空心。若簧丝为实心，则仅需令簧丝内径d₀ = 0。空心多层不同纤维混编复合材料螺旋弹簧在轴向力F下进行压缩，簧丝截面受力情况如图1所示。簧丝截面受到扭矩T和径向力F。T和F又可分解为绕t轴回转的扭矩T_t，绕b轴回转的弯矩M_b，沿t轴作用的法向力F_t和沿b轴作用的径向力F_b。

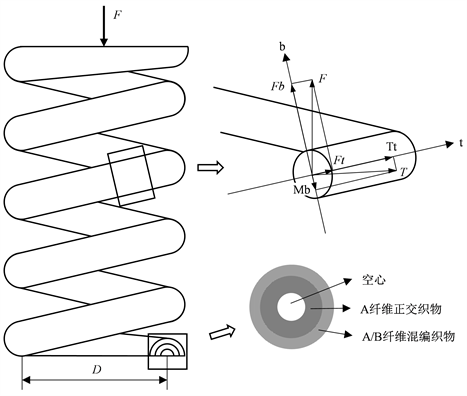
Figure 1. Diagram of spring wire section stress analysis

图1. 簧丝截面受力分析图

根据材料力学 [16] 中相关理论，当弹簧螺旋角较小时，由螺旋角引起的相关作用力M_b、F_t可忽略。并且刚度计算中，剪切力F_b作用较小可忽略。因此，简化后可以发现簧丝主要受扭矩T_t作用。簧丝截面在扭矩作用下的剪切应力τ分布如图2所示。图中d₀、d_k分别表示簧丝的内径、外径；d_i表示第i层的簧丝直径。剪切应力τ表达式为：

Figure 2. The distribution diagram of τ corresponding to T_t

图2. 与T_t对应的τ分布图

$\tau =\frac{16FDr}{\pi \left(d_k^4-d_0^4\right)}$ (1)

式中：r—簧丝横截面上应力所在点到圆心的距离；D—弹簧中径。

簧身单位体积变形能：

$u_i=\frac{{\tau }^2}{2G_i}$ (2)

式中：G_i—第i层的等效剪切模量。

弹簧整体的变形能：

$U={\displaystyle {\int }_{V}u\text{d}V}={\displaystyle \underset{i=0}{\overset{k}{\sum }}{\displaystyle {\int }_0^{n\pi D}{\displaystyle {\int }_0^{2\pi }{\displaystyle {\int }_{d_i/2}^{d_{i+1}/2}{u}_{i+1}r\text{d}r\text{d}\theta \text{d}s}}}}$ (3)

式中：rdrdθ—簧丝截面上的微分面积；ds—沿簧丝轴线的微分长度；n—弹簧有效圈数。

将式(1) (2)代入式(3)，计算结果为：

$U={\displaystyle \underset{i=0}{\overset{k}{\sum }}\frac{4\text{n}{F}^2{D}^3\left(d_{i+1}^4-d_i^4\right)}{G_{i+1}{\left(d_k^4-d_0^4\right)}^2}}$ (4)

在压缩变形x下，载荷F对弹簧所做的功W：

$W=\frac{1}{2}Fx$ (5)

根据能量守恒原理，载荷F对弹簧所做的功W等于弹簧整体的变形能U。由式(4)等于式(5)，可得弹簧刚度表达式为：

$K=\frac{F}{x}=\frac{1}{{\displaystyle \underset{i=0}{\overset{k}{\sum }}\frac{8\text{n}{D}^3\left(d_{i+1}^4-d_i^4\right)}{G_{i+1}{\left(d_k^4-d_0^4\right)}^2}}}$ (6)

由式(6)可知，关键在于得到每层等效剪切模量。对于混编织物复合材料单层等效剪切模量的计算，本文基于细观力学将其分两步进行推导。为简化模型做如下假设：1) 各组分材料间黏结牢固，界面无孔隙。2) 纤维形状和分布是规则的。

首先，单向纤维混杂复合材料工程常数可以通过混合规则进行预测。将单向板置于图3所示坐标中，1方向为纤维轴向，2方向为纤维径向，3方向垂直于1、2方向构成的平面。

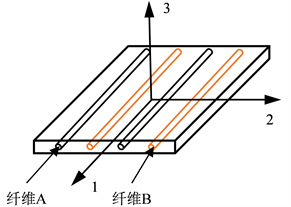
Figure 3. Schematic diagram of unidirectional fiber hybrid composites

图3. 单向纤维混杂复合材料板示意图

弹性模量：

$E_1=k_1\left(E_f{V}_f+E_m{V}_m+E_s{V}_s\right)$ (7)

$E_2=E_3=E_{\text{m}}\frac{1+\xi \eta \left(V_f+V_s\right)}{1-\eta \left(V_f+V_s\right)}$ (8)

其中

$\eta =\frac{\left(E_f{V}_f+E_s{V}_s\right)/\left(V_f+V_s\right)/E_m-1}{\left(E_f{V}_f+E_s{V}_s\right)/\left(V_f+V_s\right)/E_m+\xi }$ (9)

剪切模量：

$G_{12}=G_{13}=\left(1-C\right)\frac{1}{V_f/G_f+V_m/G_m+V_s/G_s}+C\left(G_f{V}_f+G_m{V}_m+G_s{V}_s\right)$ (10)

$G_{23}=\frac{G_m}{1-\sqrt{V_f+V_s}\left(1-G_m\left(V_f+V_s\right)\right)/\left(G_f{V}_f+G_s{V}_s\right)}$ (11)

泊松比：

${\mu }_{12}={\mu }_{13}=\frac{E_2}{E_1}{\mu }_{21}=\frac{E_2}{E_1}{k}_2\left({\mu }_f{V}_f+{\mu }_m{V}_m+{\mu }_s{V}_s\right)$ (12)

${\mu }_{23}=\frac{E_2}{2G_{23}}-1$ (13)

式中， $E_f、E_s、E_m$ 分别为A纤维、B纤维、基体弹性模量； $E_1、E_2、E_3$ 分别为单向板1方向、2方向、3方向弹性模量； $V_f、V_s、V_m$ 分别为A纤维、B纤维、基体体积分数； $\xi$ 为纤维增强作用系数(本文算例中取2)； $G_f、G_s、G_m$ 分别为A纤维、B纤维、基体剪切模量；C为纤维接触系数(本文算例中取0.22)； $G_{12}、G_{13}、G_{23}$ 分别为单向板12面、13面、23面剪切模量； ${\mu }_f、{\mu }_s、{\mu }_m$ 分别为A纤维、B纤维、基体泊松比； ${\mu }_{12}、{\mu }_{13}、{\mu }_{23}$ 分别为单向板12面、13面、23面泊松比； $k_1、k_2$ 分别为弹性模量修正系数(本文算例中取0.9)、泊松比修正系数(本文算例中取0.975)。

然后，计算正交纤维混编织物复合材料弹性常数。在分析单层正交织物复合材料弹性力学行为时可以将复合材料织物看作两层单向复合材料按纤维相互垂直的方向叠合在一起。如图4所示，以正交纤维方向为x轴(织物经向)和y轴(织物纬向)，建立坐标系。

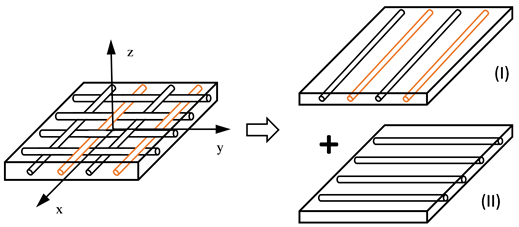
Figure 4. Schematic diagram of orthogonal hybrid braided composite plate

图4. 正交混编织物单层板示意图

弹性模量：

$E_x=k_3\left(E_{{}_1}^{\mathrm{Ⅰ}}{V}_x+E_{{}_2}^{\mathrm{Ⅱ}}{V}_y\right)$ (14)

其中

$V_x=\frac{n_x}{n_x+n_y},V_y=\frac{n_y}{n_x+n_y}$ (15)

$E_y=k_3\left(E_{{}_1}^{\mathrm{Ⅱ}}{V}_y+E_{{}_2}^{\mathrm{Ⅰ}}{V}_x\right)$ (16)

$E_z=E_{{}_3}^{\mathrm{Ⅰ}}{V}_x+E_3^{\mathrm{Ⅱ}}{V}_y$ (17)

剪切模量：

$G_{xy}=k_3\left(G_{{}_{12}}^{\mathrm{Ⅰ}}{V}_x+G_{{}_{12}}^{\mathrm{Ⅱ}}{V}_y\right)$ (18)

$G_{xz}=G_{yz}=G_{{}_{23}}^{\mathrm{Ⅰ}}{V}_x+G_{{}_{23}}^{\mathrm{Ⅱ}}{V}_y$ (19)

泊松比：

${\mu }_{xy}=\left({\mu }_{{}_{12}}^{\mathrm{Ⅰ}}{V}_x+{\mu }_{{}_{12}}^{\mathrm{Ⅱ}}{V}_y\right)\frac{\left(E_{{}_2}^{\mathrm{Ⅰ}}{V}_x+E_{{}_2}^{\mathrm{Ⅱ}}{V}_y\right)}{E_y}$ (20)

${\mu }_{xz}={\mu }_{yz}={\mu }_{{}_{23}}^{\mathrm{Ⅰ}}{V}_x+{\mu }_{{}_{23}}^{\mathrm{Ⅱ}}{V}_y$ (21)

式中， $E_1^{\mathrm{Ⅰ}}、E_2^{\mathrm{Ⅰ}}、E_3^{\mathrm{Ⅰ}}、G_{12}^{\mathrm{Ⅰ}}、G_{23}^{\mathrm{Ⅰ}}、{\mu }_{12}^{\mathrm{Ⅰ}}、{\mu }_{23}^{\mathrm{Ⅰ}}$ 分别为I层单向板1方向弹性模量、2方向弹性模量、3方向弹性模量、12平面内剪切模量、23平面内剪切模量、12面泊松比、23面泊松比； $E_1^{\mathrm{Ⅱ}}、E_2^{\mathrm{Ⅱ}}、E_3^{\mathrm{Ⅱ}}、G_{12}^{\mathrm{Ⅱ}}、G_{23}^{\mathrm{Ⅱ}}、{\mu }_{12}^{\mathrm{Ⅱ}}、{\mu }_{23}^{\mathrm{Ⅱ}}$ 分别为Ⅱ层单向板1方向弹性模量、2方向弹性模量、3方向弹性模量、12平面内剪切模量、23平面内剪切模量、12面泊松比、23面泊松比； $V_x、V_y$ 分别为单层织物经向纤维含量和纬向纤维含量； $n_x、n_y$ 分别表示单位宽度中正交织物经向和纬向相对纤维量； $E_x、E_y、E_z$ 分别为单层织物x方向、y方向、z方向弹性模量； $G_{xy}、G_{xz}、G_{yz}$ 分别为单层织物xy面、xz面、yz面剪切模量； ${\mu }_{xy}、{\mu }_{xz}、{\mu }_{yz}$ 分别为单层织物xy面、xz面、yz面泊松比； $k_3$ 为织物波纹影响系数(本文算例中取0.9)。

当复合材料板主方向与坐标轴 x 成θ角时，其主方向的剪切模量为

$G_{\theta }=\frac{G_{xy}}{1+\left[\frac{G_{xy}\left(1+{\mu }_{xy}\right)}{E_x}+\frac{G_{xy}\left(1+{\mu }_{xy}\right)}{E_y}-1\right]{\sin }^{2}2\theta }$ (22)

3. 实验测试

本文混编复合材料螺旋弹簧簧丝用直径3 mm的聚氨酯棒作为芯轴，中间层正交编织3层玄武岩纤维(1200 tex，金华石金)，最外层使用NiTi丝(直径0.5 mm，佩尔科技)和玄武岩纤维混合编织。通过真空辅助树脂传递成型工艺，用环氧树脂(AM-8960A/B)将簧丝浸润，并制作弹簧成型模具完成试样成型。工艺流程如图5所示。

使用 MTS 万能试验台以2 mm/min的压缩速率对螺旋弹簧样件进行准静态压缩试验。经过五次重复测试，获得的力-位移曲线如图6所示。在压缩位移约4 mm的位置，弹簧支撑圈与有效圈开始接触，由于制作误差导致短暂的接触不稳定，弹簧的力-位移曲线出现一小段波动，随后便呈正常线性趋势。

4. 对比分析

取弹簧压缩的力–位移曲线线性段斜率计算弹簧刚度，平均值为8.85 N/mm。实验中弹簧样件使用的材料参数、弹簧结构参数分别见表1和表2。使用马弗炉在650℃下燃烧2 h，测量出的玄武岩纤维体积分数如表3所示。根据第2节推导的理论模型编写matlab程序，计算得到弹簧刚度值为8.61 N/mm，与试验结果对比误差为2.7%，证明了刚度预测模型的正确性以及计算结果的精确性。

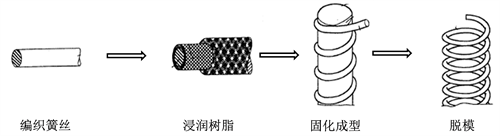
Figure 5. Schematic diagram of spring specimen manufacturing process

图5. 弹簧试样制作流程示意图

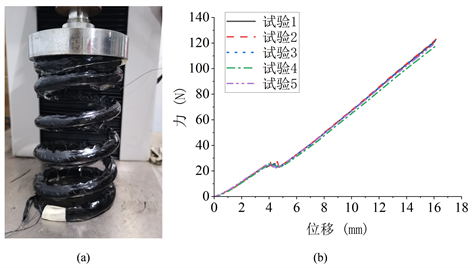
Figure 6. Compression test (a) Test photo; (b) Force-displacement curve

图6. 压缩试验(a) 试验照片；(b) 力-位移曲线

Table 1. Material parameters for spring

表1. 弹簧的材料参数

Table 2. Structural parameters of spring

表2. 弹簧的结构参数

Table 3. Fiber volume fraction of different layers

表3. 不同层纤维体积分数

5. 结论

本文基于复合材料细观力学方法，对单向纤维混杂复合材料的工程常数进行理论计算，扩展正交纤维混杂织物复合材料的工程常数计算公式结合传统螺旋弹簧刚度推导方法，最终提出多层不同纤维混编复合材料螺旋弹簧的刚度预测模型。并且制作多层NiTi丝和玄武岩纤维混编复合材料螺旋弹簧样件进行压缩试验，通过对比分析，得出理论预测与实验结果误差为2.7%，表明该理论预测方法的正确性以及计算结果的精确性。

提出的植入NiTi-玄武岩纤维混编纤维增强体的复合材料螺旋弹簧刚度预测模型不仅为螺旋式混编复合材料结构的刚度计算问题提供了新思路，为多层异种纤维混杂复合材料螺旋弹簧的工程应用奠定了基础，而且为多层异种纤维混杂复合材料管式结构的刚度性能预测提供了参考。

基金项目

国家自然科学基金项目(52102430)。