基于陶瓷复合材料的盘式制动器热力耦合仿真分析

Thermo-Mechanical Coupling Simulation Analysis of Disc Brake Based on Ceramic Composite Material

摘要: 针对盘式制动器在制动过程中温度分布不均而产生过大热变形，甚至出现热疲劳裂纹、磨料脱落等问题，利用ANSYS Workbench平台建立SiCP/Al陶瓷复合材料盘式制动器热力耦合模型，探究了不同制动力和制动速度下制动盘温度、位移、应力的变化规律，并将计算结果与传统金属制动盘进行对比。结果表明：在额定速度下，随着制动压力的等量增加，温度及应力的最大值均随着制动压力的等量增加而非线性增加，位移沿径向方向呈现出先增大后减小的趋势；随着制动速度的增加，温度的差异明显增大，最大应力与位移均出现在制动盘与摩擦片接触处；与传统材料制动盘相比SiCP/Al陶瓷复合材料制动盘制动效果更加明显且制动性能更稳定。相关结果可为盘式制动器的安全运行和优化设计提供技术参考。

Abstract: Aiming at the problems of excessive thermal deformation and even thermal fatigue cracks and abrasive shedding caused by uneven temperature distribution of disc brake during braking, the thermal coupling model of SiCP/Al ceramic composite disc brake is established by using the ANSYS Workbench platform, and the change laws of brake disc temperature, displacement and stress un-der different braking forces and braking speeds are investigated, and the calculated results are compared with those of traditional metal brake discs. The results show that at the rated speed, with the equal increase of the brake pressure, the maximum values of temperature and stress increase nonlinearly with the equal increase of the brake pressure, and the displacement first increases and then decreases along the radial direction; With the increase of braking speed, the temperature dif-ference increases significantly, and the maximum stress and displacement appear at the contact of brake disc and friction plate; Compared with traditional brake discs, SiCP/Al ceramic composite brake discs have more obvious braking effect and more stable braking performance. The relevant results can provide technical reference for the safe operation and optimal design of the disc brake.

1. 引言

制动器作为车辆制动系统的关键零部件之一，其制动性能直接关系到车辆的运行安全 [1] 。目前市场上主流的有盘式制动器和鼓式制动器，盘式制动器因其稳定性强、结构简单等优点，在乘用车领域已占据主导性地位 [2] 。汽车制动盘多采用铸铁材料，但是铸铁的性能对温度十分敏感，随着温度的升高制动盘会出现热疲劳、热衰退等现象 [3] 。SiC_P/Al陶瓷复合材料具有密度低、热膨胀系数小、耐高温、耐疲劳等特点，在航空航天、交通运输等领域有着广泛的应用 [4] 。因此对陶瓷复合材料盘式制动器进行热力耦合仿真有重要的理论意义和应用价值。

目前汽车制动盘应用最广泛的是铸铁材料，但是由于适用温度的限制，铸铁材料在高速情况下容易出现热疲劳等现象，为此近年来，国内外广泛开展了对高性能摩擦材料的研究。Ma等 [5] 制备了不同纤维的纸基摩擦材料，并分析了碳纤维增强摩擦材料在不同工况下的摩擦磨损性能。Li等 [6] 研究了Si₃N₄陶瓷材料在不同环境温度下的摩擦磨损行为和不同表面质量的材料去除机理，并与普通金属材料进行对比，结果证明Si₃N₄陶瓷材料具有更良好的力学稳定性。Si等 [7] 以各种硬质颗粒为摩擦相制备了SiO₂/SiC/Al₂O₃铜基摩擦材料，并探究了温度对摩擦材料摩擦学行为的影响。Wei等 [8] 开发了两种使用碳纤维或碳纳米管替代铜纤维的无铜制动材料，并评估了它们的摩擦学性能、颗粒排放和制动尖叫噪声，得出了无铜制动材料比含铜制动材料具有更大的比磨损率。Jubsilp等 [9] 制备了UFNBRPs摩擦复合材料，所制备的材料拥有较高的摩擦系数和耐磨性，符合汽车刹车片的工业标准。

此外针对盘式制动器，采用热力耦合技术分析应力场与温度场之间的作用关系是当前的主要研究手段。Wen [10] 在ABAQUS中建立了客车盘式制动器的三维模型，并对盘式制动器的温度场进行了数值模拟，得出了不同制动条件下的制动盘表面温度分布特性。Belhocine等 [11] 使用ANSYS软件对两种类型制动盘进行了数值建模，并采用热–结构耦合方法进行了瞬态热分析和静态结构分析，最后将两种类型制动盘的模拟结果进行对比。Yevtushenko等 [12] 提出了一种确定多盘系统中单个制动盘温度的解析模型，并利用热力耦合方法进行了数值模拟，得出了制动过程中，环境传热、纤维束长度和复合材料中纤维浓度对制动盘温度的影响。Yuan等 [13] 基于均匀分布热源法，提出了一种利用余弦函数预测制动温度的更准确有效的方法，并将其温度曲线与热力耦合法的曲线进行对比，所得结果完全匹配。Modanloo等 [14] 在均匀压力和均匀摩擦两种摩擦热载荷条件下，建立了高速车辆盘式制动器的热传导模型，并采用变量分离法在圆柱坐标系下求解控制热传导方程。

综上所述，目前国内外主要致力于传统金属盘式制动器的热–应力耦合场问题的研究，而关于陶瓷复合材料盘式制动器在制动工况下的热力耦合分析鲜见开展，因此本文模拟分析了SiC_P/Al复合陶瓷材料盘式制动器在制动工况下温度、位移及应力变化特性，为盘式制动器的优化设计提供新的可行思路，以期进一步降低制动器损耗。

2. 热力耦合理论

2.1. 热力分析条件假设

为了保证热力耦合计算的正确性与独立性，做出如下假设：

1) 摩擦片与制动盘材料均为各向同性，在制动过程中没有发生塑性形变；

2) 制动过程中的动能全部转化为摩擦热且没有热量散失；

3) 在温度变化情况下，相应的热传导系数和比热容保持固定；

4) 摩擦片与制动盘之间的接触面为理想平面，环境初始温度为T = 20˚。

2.2. 耦合模型

在制动力较大的情况下，制动盘和摩擦片之间的摩擦热几乎全部转化成摩擦副接触点处的热能，此时摩擦副接触点处单位面积内的热载荷为：

$q\left(r,\theta ,t\right)=\mu \cdot p\left(r,\theta ,t\right)\cdot v\left(r,\theta ,t\right)$ (1)

式中r，θ为径向坐标和周向坐标；t为制动时间； $q\left(r,\theta ,t\right)$ 为热流密度；μ为接触面摩擦系数； $p\left(r,\theta ,t\right)$ 为制动时摩擦片和制动盘的接触压强； $v\left(r,\theta ,t\right)$ 为摩擦片与制动盘之间的相对滑动速度。

制动盘和摩擦片的热流分配系数可通过理论公式计算获得：

$\eta =\sqrt{\frac{{\rho }_a{c}_a{\lambda }_a}{{\rho }_d{c}_d{\lambda }_d}}$ (2)

式中 ${\rho }_a$ 、 $c_a$ 、 ${\lambda }_a$ 分别为摩擦片的密度、比热容、热传导系数； ${\rho }_d$ 、 $c_d$ 、 ${\lambda }_d$ 分别为制动盘的密度、比热容、热传导系数。

则作用于制动盘上的热流密度为：

$q_1=q\times \frac{\eta }{1+\eta }$ (3)

式中q为摩擦副内的热载荷。

根据热传导定律和能量守恒原理建立制动盘和摩擦片的温度场热传导方程为：

$\frac{\partial T}{\partial \text{t}}=\frac{\lambda }{\rho c}\left(\frac{{\partial }^{2}T}{{\partial }^2{r}^2}+\frac{{\partial }^{2}T}{{\partial }^2{\theta }^2}+\frac{{\partial }^{2}T}{{\partial }^2{t}^2}\right)$ (4)

式中λ为瞬态温度；T为制动盘温度。

制动盘和摩擦片之间的换热主要为对流换热，制动盘表面的对流换热系数可表示为：

$h=\{\begin{array}{c}0.7\left({\lambda }_e/d_a\right)R_e^{0.05}\begin{array}{cc}& R_e\le 2.4\times {10}^5\end{array}\\ 0.7\left({\lambda }_e/d_a\right)R_e^{0.8}\begin{array}{cc}& R_e>2.4\times {10}^5\end{array}\end{array}$ (5)

式中 $R_e$ 为雷诺数； $d_a$ 为制动盘的直径； ${\lambda }_e$ 为空气传热系数。

3. 有限元建模

3.1. 几何参数及材料属性

SiC_P/Al陶瓷材料制动盘和复合材料摩擦片的几何参数如表1所示，材料属性如表2所示。

Table 1. Geometric parameters of brake disc and friction plate

表1. 制动盘与摩擦片几何参数

Table 2. Brake disc and friction plate material properties

表2. 制动盘与摩擦片材料属性

3.2. 实体建模

采用三维软件Solidworks建立SiC_P/Al陶瓷材料制动盘的几何模型，为了方便网格剖分及模型计算，在建模过程中采用实心制动盘且对模型的局部结构进行简化，简化后的模型如图1所示。

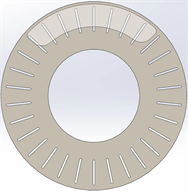
Figure 1. 3D simplified model of SiC_P/Al ceramic composite brake disc

图1. SiC_P/Al陶瓷复合材料制动盘三维简化模型

3.3. 网格划分

有限元网格划分是热力耦合分析的关键，三维模型离散后的网格质量及数量直接影响到求解时长和结果精度。为了准确反映盘式制动器内各部件的受力和变形，本文将模型导入ANSYS的mesh模块，采用六面体和四面体混合的方式对制动器模型进行网格划分，其中制动盘包含的单元数为26,584，节点数为95,624，生成的制动器网格模型如图2所示。

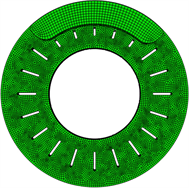
Figure 2. Element model of SiC_P/Al ceramic composite brake disc

图2. SiC_P/Al陶瓷复合材料制动盘有限元模型

3.4. 边界条件及约束

本文将APDL语言加入到ANSYSWorkbench中来完成热力耦合边界条件及约束设置，具体方法为：在Workbench的Engineering Data和Geometry模块中添加材料等工程数据，通过插入命令“et,1,solid226,11”修改单元类型，在contacts中插入命令“keyopt,cid,1,1”来建立制动器摩擦时候的需要添加的结构与温度的自由度；“Terf,20”将初始温度设置为20℃；“Trnopt,Full”定义瞬态分析方法为完全法。

4. 盘式制动器模拟仿真及结果分析

4.1. 制动力对热力耦合特性的影响

为了探究制动力大小对SiC_P/Al陶瓷复合材料制动盘热力耦合特性的影响，本文以0.5 MPa为增量，开展了在额定制动速度v = 80 km/s作用时三种制动力下的制动盘热力耦合特性分析，在制动力为4.5 MPa、5 MPa、5.5 MPa时，制动盘温度、应力的瞬态响应曲线如图3所示。

图3为摩擦片中心区域某点在不同制动力下温度变化曲线。可以看出，在不同制动力下，温度响应曲线变化基本相同，均呈非线性锯齿状先上升后下降的趋势；温度的最大值均随着制动力的等量增加而非线性增加，增幅随制动压力的增加呈现先变大后减小的变化规律；0~1 s时各温度曲线增长速率较快，从1~2 s时增长速率逐渐放缓，2 s开始呈下降趋势，这是由于在0~1 s时处于压力施加的初期，摩擦生热远大于对流换热，摩擦副的摩擦区域温度急剧上升，2 s时制动压力施加完毕，摩擦区温度缓慢上升至最高点。制动压力为4.5 MPa、5 MPa、5.5 MPa对应的最大温度分别为191.46℃、203.32℃、216.78℃，表明制动压力对摩擦温度的影响表现出先增大后减小的趋势。

图4为不同制动力下应力响应曲线，不难得知：应力响应曲线表现出与温度曲线相似的变化规律，均呈现出先增大后减小的趋势；当t = 0.5 s时由于受到制动力的作用，应力上升速度较快，当t处于1.5 s时随着摩擦热的增大热应力继续增加，在t在2.2 s附近时出现最大热应力点，当t = 2.2 s之后制动盘表面温度下降，热应力也逐渐减小；制动压力越大，制动盘表面应力增长速率越快且应力值越高，制动压力为4.5 MPa、5 MPa、5.5 MPa对应的最大应力分别为194.23 MPa、201.62 MPa、227.78 MPa。

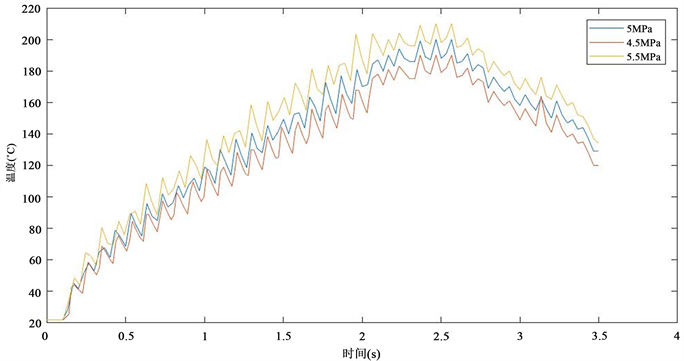
Figure 3. Temperature response curve of SiC_P/Al ceramic composite brake disc under different braking forces

图3. 不同制动力下SiC_P/Al陶瓷复合材料制动盘温度响应曲线

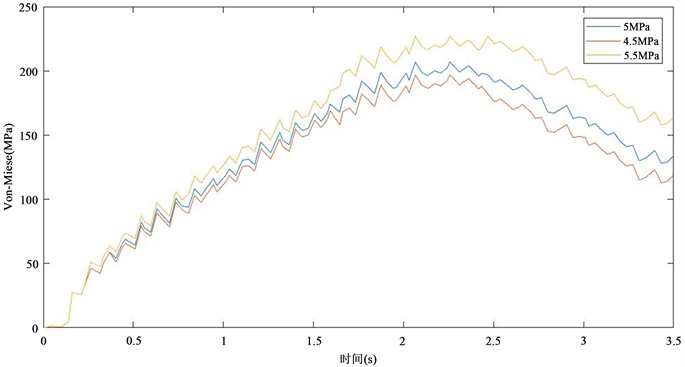
Figure 4. Stress response curve of SiC_P/Al ceramic composite brake disc under different braking forces

图4. 不同制动力下SiC_P/Al陶瓷复合材料制动盘应力响应曲线

左图5(a)为制动压力4.5 MPa时SiC_P/Al陶瓷复合材料制动盘径向位移最大时刻的分布云图，可以看出，制动盘位移从中心孔位置外缘处呈现先增大后减小的趋势，最大位移发生在摩擦片中心区域，这是由于此处施加了制动力且刚度较小，从而形成摩擦接触挤压区域并在制动盘径向产生较大变形。图5(b)为位移最大时刻2.0 s时分别对应的径向方向的位移变化，由图可知：不同制动压力下位移的增幅总体上呈现由摩擦片中心区域向两侧衰减的变化趋势，这表明制动压力对位移的影响沿径向方向先增大后减小；同一相对径向长度处的最大位移增幅随制动压力的增加呈现先变大后减小的趋势，表明随着制动压力的增大，压力对制动盘位移的贡献先上升后下降。

(a) 4.5 MPa时制动盘位移分布云图 (b) 径向方向的位移变化曲线

Figure 5. Displacement distribution of SiC_P/Al ceramic composite brake disc at 2.0 s

图5. 2.0 s时SiC_P/Al陶瓷复合材料制动盘位移分布

4.2. 制动速度对热力耦合特性的影响

制动速度也是影响SiC_P/Al陶瓷复合材料制动盘热力耦合特性的主要因素之一。在额定制动力4.5 MPa情况下设置制动初速度分别为80 km/h、100 km/h、120 km/h，探究制动盘温度、应力响应，其曲线如图所示。

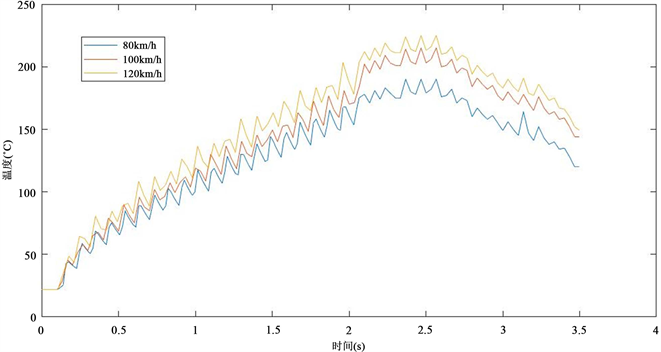
Figure 6. Temperature response curve of SiC_P/Al ceramic composite brake disc under different braking speeds

图6. 不同制动速度下SiC_P/Al陶瓷复合材料制动盘温度响应曲线

图6为不同制动速度下温度变化曲线，从图中可以得出在制动的初始阶段，三条曲线接近重合，这说明在此阶段制动速度对温度的影响不大，随着时间的延长，三条曲线之间的温度差异明显增大，说明制动初速度此时对制动温度影响较大，当t = 2 s时热交换速度与热流输入速度相近，温度上升的趋势变缓；不同制动速度下的温度响应均呈现了先增大后减小的趋势，并且其变化速率随制动速度的增加而增加。制动初速度为80 km/h、100 km/h、120 km/h时对应的最高温度分别为193.52℃、207.26℃、228.45℃。

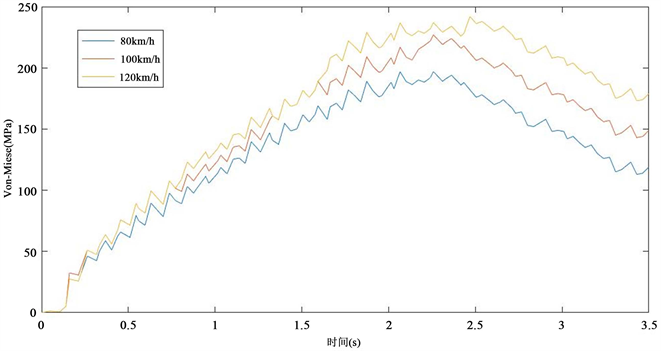
Figure 7. Stress response curve of SiC_P/Al ceramic composite brake disc under different braking speeds

图7. 不同制动速度下SiC_P/Al陶瓷复合材料制动盘应力响应曲线

图7为不同制动速度下应力响应曲线，由曲线可知，当t < 0.5 s时各速度下制动盘产生的热变形都较小，因此热应力也较小。当t > 0.5 s时三条曲线都快速上升，但低制动速度的曲线增长较为缓慢，当t在2 s附近时三条曲线均缓慢增长至最高点且热应力差异变小。最大应力区域出现在制动盘与摩擦片接触处，并基本呈向两侧衰减的趋势，制动初速度为80 km/h、100 km/h、120 km/h时对应的最大应力分别为197.63 MPa；225.34 MPa；251.34 MPa。随着制动速度增加热应力先增大后减小，而相邻制动速度下应力最大值的增幅不断减小，这表明制动速度对应力贡献随之增加而降低。

(a) 100 km/h时制动盘位移分布云图 (b) 径向方向的位移变化曲线

Figure 8. Displacement distribution of SiC_P/Al ceramic composite brake disc at 2.1 s

图8. 2.1 s时SiC_P/Al陶瓷复合材料制动盘位移分布

在位移最大时刻2.1 s，制动速度100 km/h时的SiC_P/Al陶瓷复合材料制动盘径向位移分布云图如图8(a)所示，三种制动速度下制动盘位移分布见图8(b)，可以看出：最大位移区域亦出现在摩擦片与制动盘接触处，并向两侧衰减，随着制动速度的增加，该趋势更为明显；不同制动速度下沿径向方向最大位移差值在摩擦片与制动盘接触处达到最大，这表明了制动速度对位移的影响在最大位移处达到峰值。

4.3. 陶瓷复合材料制动盘热力耦合分析对比

为了验证SiC_P/Al陶瓷复合材料制动盘的良好性能，将SiC_P/Al陶瓷复合材料制动盘与传统材料制动盘在紧急制动工况下温度、位移及应力的变化规律和分布特点进行对比，结果如下图所示。

(a) 0.5 s (b) 2.0 s

Figure 9. Temperature nephogram of traditional material brake disc at different times

图9. 不同时刻传统材料制动盘温度云图

(a) 0.5 s (b) 2.0 s

Figure 10. Temperature nephogram of SiC_P/Al ceramic composite brake disc at different times

图10. 不同时刻SiC_P/Al陶瓷复合材料制动盘温度云图

图9和图10为传统材料制动盘及SiC_P/Al陶瓷复合材料制动盘在0.5 s和2.0 s时刻的温度变化云图，从图中可以看出，制动盘与摩擦片在作相对摩擦的过程中，制动盘表面温度沿径向由外到内逐渐降低，传统材料制动盘在0.5 s时刻摩擦区最大温度为36℃，在2.0时刻摩擦区最大温度为185℃，而SiC_P/Al陶瓷复合材料制动盘在0.5 s时刻摩擦区最大温度为54℃，在2.0时刻摩擦区最大温度为204℃。通过对比可以发现由于SiC_P/Al陶瓷复合材料的摩擦因数较高，在相同时刻内摩擦区的最大温度值更高，这表明在相同的刹车行程时间内采用SiC_P/Al陶瓷复合材料制动盘能够将更多的汽车动能转化为热能，刹车制动效果更明显。但是因为SiC_P/Al陶瓷复合材料刹车片的温度场在径向上存在较大温度梯度，所以会加剧摩擦片的变形以及制动盘的磨损。

图11为传统材料制动盘及SiC_P/Al陶瓷复合材料制动盘在0.5 s时刻的位移变化云图，从中可以发现，传统材料制动盘与SiC_P/Al陶瓷复合材料制动盘在制动过程中沿制动盘接触面垂直方向的位移近似相等且二者最大位移均出现在制动盘端面外圆处。这说明在汽车制动过程中，制动盘位移与所使用材料类型无关。

(a) 0.5 s时传统材料制动盘位移云图 (b) 0.5 s时SiC_P/Al陶瓷复合材料制动盘位移云图

Figure 11. Temperature nephogram of SiC_P/Al ceramic composite brake disc at different times

图11. 0.5 s时传统材料制动盘与SiC_P/Al陶瓷复合材料制动盘位移云图

(a) 0.5 s (b) 2.0 s

Figure 12. Stress nephogram of traditional material brake disc at different times

图12. 不同时刻传统材料制动盘应力云图

(a) 0.5 s (b) 2.0 s

Figure 13. Stress nephogram of SiC_P/Al ceramic composite brake disc at different times

图13. 不同时刻SiC_P/Al陶瓷复合材料制动盘应力云图

图12和图13为在紧急制动过程中传统材料制动盘及SiC_P/Al陶瓷复合材料制动盘处于0.5 s和2.0 s时刻的应力变化云图。从图中可以看出在制动过程中，传统材料制动盘在0.5 s时应力最大值达到49 MPa，在2.0 s时应力最大值达到203 MPa且沿周向分布在摩擦接触区域中。而SiC_P/Al陶瓷复合材料制动盘在0.5s时应力最大值为26 MPa，在2.0 s时应力最大值为156 MPa，相较而言配置SiC_P/Al陶瓷复合材料的制动盘热应力明显降低，应力分布也更加均匀，因此其在制动过程中更不易发生断裂，轴向变形量更小，制动性能更加稳定。

利用文献对比验证的方法对本文研究结果进行验证。文献 [15] 所用的试验模型与本文中建立的模型皆为通风制动盘，且制动盘都采用TH250传统材料。该文献利用Link3900 NVH平台的台架试验方法，得到温度传感器节点与有限元模型对应节点的温度，当制动初速度为90 km/h、制动速度为2 s时，节点温度为185.2℃。本文以80 km/h、100 km/h为制动初速度，制动2 s时制动温度为186.35℃、193.23℃，取其两者平均值作为90 km/h制动最高温度进行分析，则温度为189.79℃，与文献 [15] 的平均偏差为2.5%。由于对流换热及热传导的施加参数存在差异，因此本文与文献 [15] 存在较小的偏差。从仿真和试验结果的数据误差看，本文的模拟方法具有较高的准确性和可靠性。

5. 结论

本文针对SiC_P/Al陶瓷复合材料盘式制动器，建立了其有限元模型，在考虑热力耦合作用的情形下，开展了不同制动力和制动速度下陶瓷复合材料盘式制动器热力耦合分析，得到结论如下：

1) 不同制动力下，制动盘温度和应力响应曲线变化规律类似，两者均呈现先增大后减小的趋势；温度及应力的最大值均随着制动压力的等量增加而非线性增加；制动盘位移沿径向方向呈现出先增大后减小的趋势。

2) 不同制动速度下的温度响应均呈现了先增大后减小的趋势，并且其变化速率随制动速度的增加而增加；最大热应力出现在制动盘与摩擦片接触处，并基本呈向两侧衰减的趋势；不同制动速度下沿径向方向最大位移差值在摩擦片与制动盘接触处达到最大。

3) 相较于传统材料制动盘，SiC_P/Al陶瓷复合材料的摩擦因数较高，在相同时刻内摩擦区的最大温度值更高，因此采用SiC_P/Al陶瓷复合材料刹车片能够将更多的汽车动能转化为热能，刹车制动效果更明显；SiC_P/Al陶瓷复合材料的制动盘热应力较低，应力分布也更加均匀，因此其在制动过程中更不易发生断裂，制动性能更加稳定。