1. 引言
近年来为不断丰富人们的业余生活，国家经常举办一些体育赛事和艺术活动，为了提高观众的观赏质量，并在最大限度内承载观众数量，各项活动的主办方基本都使用了临时组装式看台来解决较大客流量这一问题。但是，目前国内的临时看台结构依旧存在着设计不合理的问题，其研究体系也不尽完善，因此导致在其实际使用过程中，引发了一系列安全事故，如：2007年上海国际赛车场4个临时看台倒塌和2002年张学友武汉演唱会临时看台倒塌 [1] ；2004年9月12日，中国网球公开赛某场预选赛的观众席顶部数十个座椅被风吹翻。因此临时看台仍面临着技术上的不足，其安全性受到了市场的质疑。目前，国内只确定了临时看台的露天风荷载系数 [2] ，但该系数并不适用于大型临时看台的风荷载计算。哈尔滨工业大学研究者提出了可变迎风面对大型临时看台表面风压的干扰特征，其观点的提出对于研究大型临时看台的荷载分布具有着重要意义 [3] 。William B.等 [4] 经过研究制定了临时结构的设计规范，Jamshid等 [5] 提出了临时结构风荷载计算的准确方法，通过采用对永久结构的风荷载予以一定折减的方式，从而对多数永久结构抗风载荷进行了一定程度的缩减，并由此来推测临时搭建结构的抗风载荷的大小，所以对于临时搭建结构抗风载荷的具体公式及可靠的标准都未得到统一。另外国外的技术人员对一些大型临时看台的安全疏散也作出了众多研究，其中Togawa等 [6] 对大型看台在遭遇火灾时人员疏散的过程进行了研究，并建立了Togawa行人疏散模型，在一定程度上缩减了大型看台面临火灾时人们的疏散时间。另外Guo等 [7] 在考虑到大型看台面临着高密度人群聚集，以及在疏散过程中相互影响的情况，利用元胞自动机建立了行人疏散仿真模型。此外，Zhao H.，Gao Z等 [8] 人对人员疏散过程进行了统计分析与模型建立，但由于忽略了疏散过程中人们的交通特性易受时间的推移而发生变化这一特点，因此该项研究无法准确映射在疏散过程中人流的动态特性。意识到国外学者研究的缺陷所在后，张青松等 [9] 在传统大型看台疏散计算模型的基础之上，建立了相较于之前更加先进和完善的疏散模型，其验证结果也更为准确，但是其研究模型仍然存在着过于依赖具体疏散结构的缺点，模型适配不具有普遍性。
2. 研究内容
从近几年的报道可以得知，折叠式看台仍面临着很多因技术方面不足而导致的坍塌、疏散不便等危险事件，同时看台折叠和展开时的跑偏、传动装置的噪音也对看台整体使用的舒适度有巨大的影响，所以看台细节的设计受到了日益的关注，稳固的载重装置、精确的限位装置、平稳安静的驱动装置是本设计的目的。根据《演出场所安全技术要求》(WH/T 42-2011) [10] 的标准，本文提出了一种具有可折叠结构的看台系统，由减速电机完成自动折叠或者手动折叠，可自由更改其规格，避免了传统临时看台搭建上的时间及后续拆卸问题。并且折叠式看台可以实现循环利用，符合我国绿色环保的理念。
2.1. 折叠式看台座结构设计
折叠式看台满座为150座(不包含残疾人专座)，共计5排，每排30座，看台横向宽度约为19.790 m，整体高度约为2.828 m，看台展开后纵向长度约为5.539 m，整体占地面积约为109.617 m2。折叠后纵向长度约为1.664 m，整体占地面积约为32.931 m2，看台整体的伸缩比约为3.33:1，看台展开折叠如图1(a)、图1(b)所示。
(a) 看台展开图
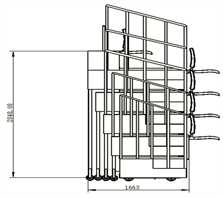(b) 看台折叠图
Figure 1. Collapse the grandstand view
图1. 折叠看台视图
根据技术要求，观众席两侧设双走廊，每排30座，共计5排，经计算排距需增大(4*25) 100 mm；座椅左右间间隔为0.09 m，排距为1.1 m，座椅椅背突出部分为0.55 m；每排走道使用排距尺寸1.1 m，两侧走道第一排最长1 m，依次缩短，第五排为0.82 m；除每层衔接处均采用整体3 mm厚的钢板；在看台最前端和顶层末端设置了安全护栏，栏杆高度在1.2 m~1.4 m之间，纵向杆安全距离在0.2 m~0.4 m之间，栏杆采用Ф38 mm钢管，钢管表面经过涂油、除锈后再做喷塑处理，栏杆与台阶相焊接，护栏扶手选择塑料材质。
折叠通过每层之间的轨道与从动轮的相对位移来完成，阶层间折叠结构如图2所示，轨道(3)两侧高度约为整个从动轮直径的1/3，防止从动轮在折叠过程中发生出轨或跑偏的现象，轨道两端处设置高度大于从动轮直径1/2的挡板(1)，在限制从动轮水平位移距离的同时，也使得每一层完成展开或者折叠后，有足够的力带动下一层台阶的继续展开或者折叠。同时这种每阶层间的叠加也将看台整体的每排受力均匀分布到看台的整体结构上。
1. 挡板；2. 从动轮；3. 轨道
Figure 2. Inter-class folding structure
图2. 阶层间折叠结构
2.2. 折叠式看台驱动装置设计(图3)
每阶层前排脚轮为2个，共计8个，看台主要的重量由驱动轮以及第2、3、4、5排的后排脚轮(最底层脚轮)承担。每阶层后排脚轮共17个，均为从动轮(牛筋轮)，整个看台共计68个从动轮，所有的脚轮均为单向轮，整个伸缩过程中脚轮只完成滚动，从而避免了采用万向轮带来的偏移问题。支撑梁与看台每阶层间设置用50 mm*50 mm*3 mm方形钢管焊接而成的支撑板，支撑板与台阶采用焊接，使每阶层受力更加均匀，有效的阻止了由于阶层过薄而产生的弯曲变形，提高了看台整体的安全性。同一阶层的每个支撑杆间都均匀分布了100 mm*50 mm*4 mm的矩形钢管的横梁，有效的阻止了由于支撑杆过长而产生的弯曲变形。支撑杆与支撑板间也采用焊接，所以看台每阶层都是一个整体，最后通过每一阶层间的组装完成。
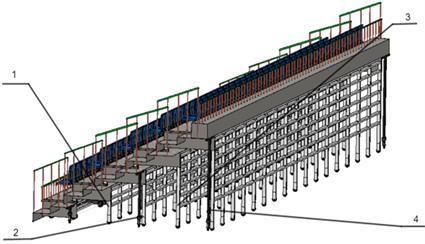1. 第二阶脚轮；2. 第三阶脚轮；3. 第四阶脚轮；4. 第五阶脚轮
Figure 3. Collapse the grandstand side view
图3. 折叠看台侧视图
看台驱动装置设置在第一阶看台的下部，如图4所示，竖支撑杆(1)与横支撑杆(4)采用螺栓连接，横向支撑杆设置了配重块(5)，确保第一阶驱动装置的每个驱动轮(2)与地面接触更加充分，提高其与地面的摩擦力。同时采用看台两侧的联动驱动，使得看台在折叠或者展开的过程中移动更加平稳，驱动装置每侧安装8个驱动轮，驱动轮选择花纹聚氨酯驱动轮，可以防止伸缩行过程中打滑。驱动轮通过一号驱动轴(3)上的链轮与减速电机(8)上的链轮采用链轮链条传动，并通过链轮链条带动传动轴(9)传递到右侧传动装置。驱动装置动力源选择TECO的BR卧式附三相铝壳马达减速电机，承受过载能力高、体积小、能耗少、震动小、噪音低；在后期，减速电机的维护更方便、维护成本较低。
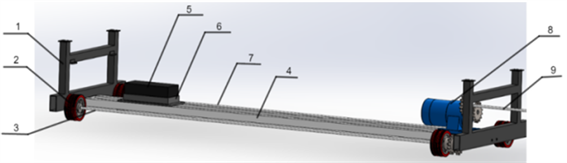1. 竖支撑杆；2. 驱动轮；3. 一号驱动轴；4. 横支撑杆；5. 配重块；6. 配重块固定框； 7. 二号驱动轴；8. 减速电机；9. 传动轴
Figure 4. First level left drive unit
图4. 第一阶层左侧驱动装置
3. 研究方法
本文采用安全系数分析法，将大型折叠式看台系统中包含的不确定性因素，放入单一的安全系数之中进行考量。安全系数的确定需要考虑荷载、材料的力学性能、试验值和设计值与实际值的差别等各种不定性。
3.1. 设计校核计算
看台整体钢板面积约为165.979 m2，钢板厚度约为3 mm，钢板密度为7980 kg/m3，则钢板总重量约为G：
(1)
式中：
s——钢板的总面积，单位m2；
h——钢板的厚度，单位m；
g——重力加速度，一般取值9.8 N/kg；
ρ——钢板的密度，一般取值7980 kg/m3；
式中s为165.979 m2，h为0.003 m，g为9.8 N/kg，ρ为7980 kg/m3，则G = 38940 N。
看台每个脚轮的恒载荷WH为：
(2)
式中：
G——钢板的总重量，单位N；
n——脚轮的个数，单位个；
此看台底部总计驱动轮16只，从动轮68只，共计84只脚轮，故WH = 47.303 kg。
当台上结构构件每点承受载荷小于或等于30 kg时，及看台处于空载状态，台上结构载荷能力应按均匀分布载荷WA：
(3)
式中：
WA——均布载荷的计算载荷，单位kg；
WE——台上结构构件各点可承受的实际载荷最小值，简称“额定载荷”，单位kg；
k1——载荷偏离系数。此看台为室内看台k1取1；
k0——安全偏离系数。k0取值1.5；
最后确定的恒载荷WH小于WE，式中k1为1，k0为1.5，WE由选型的脚轮得为255.102 kg，则WA为170.068 kg，由公式(2)知，WH为47.303 kg，及当看台空载时每只脚轮受到的恒定载荷小于额定的载荷，符合使用要求。
当台上结构构件每点承受载荷大于30 kg时，及当看台处于满载状态时，台上结构载荷能力应按集中分布载荷计算。计算如下：
(4)
式中：
WF——集中载荷的计算载荷，单位kg；
WFE——台上结构构件各点可承受的集中载荷，单位kg；
最后确定动载荷WD应该小于WF，式中k1为1，k0为1.5，WFE由选型的脚轮得为255.102 kg，则WF为170.068 kg，由公式(3)知，WD为163.36 kg，及当看台满载时每只脚轮受到的动载荷小于集中载荷，满足使用要求。
3.2. 系统参数对响应的影响
整体结构的材料选择材料库中的常用结构钢Q235，弹性模量为200 GPa，泊松比为0.3，屈服强度为255 MPa。
简化看台并对对每一个支撑杆底面进行固定约束，并对看台施加负载，看台整体均匀负载95,550 N (150个正常成年人的重量)，每阶层负载19,110 N，每个座椅负载637 N，负载均匀分布在150个薄板上，设置法向的均布载荷，如图5所示。
Figure 5. Load settings for large folding stands
图5. 大型折叠式看台的负载设置
大型折叠式看台静力学分析的应力分布如图6所示。
大型折叠式看台设置的应力类型为von Mises应力，应力最大为28.42 MPa，由于看台最上一个阶层的力是依次传递给下一阶层的，所以最大应力出现在第一阶层底部立柱与横梁处，而Q235的屈服强度为255 MPa，所以满足使用要求。
Figure 6. Stress diagram for static analysis of large folding stands
图6. 大型折叠式看台静力学分析的应力图
大型折叠式看台静力学分析的位移分布如图7所示。
大型折叠式看台的主要位移区位于第一阶层的中间部分，位移类型为合位移，由于第一阶层位于最底层，没有下一阶层的支撑，并且由于中间部位缺少辅助的支撑，从而变形相对较大，但是总位移量为1.219 mm，相较于看台的整体结构尺寸可以忽略，故满足要求。
Figure 7. Displacement diagram for static analysis of large folding stands
图7. 大型折叠式看台静力学分析的位移图
大型折叠式看台静力学分析的应变分布如图8所示。
大型折叠式看台应变类型为对等应变，最小应变为3.280*10−11，最大应变为1.088*10−4。
Figure 8. Strain diagram for static analysis of large folding stands
图8. 大型折叠式看台静力学分析的应变图
4. 结论
1) 本文提出了一种大型折叠看台系统方案，在实现基础看台功能的同时，对其最本质的观赏效果以及安全保障都做了考量，同时还避免了传统临时看台搭建上的耗时耗力及后续拆卸困难的问题，充分实现了高效循环使用。该折叠看台系统可适配于多种体育场，具有良好的兼容性。
2) 通过安全系数法对大型折叠看台进行结构设计及其尺寸的确定，在确保看台安全稳定的情况下对可承载游客数量进行了最大化设计，相比于传统中小型折叠看台，可以容纳更多的观众。该设计通过动载荷校核计算进行检验，充分验证了看台结构、尺寸设计的可靠性。
3) 通过Solidworks中的插件Simulation对大型折叠式看台框架的静力学分析计算，可以得到看台受到的最大应力位于看台第一阶层的中间部分，最大应力为28.42 MPa，与Q235的屈服强度255 MPa相比，最大应力远小于折叠看台的屈服强度，看台第一阶层中部的最大位移量为1.219 mm，看台每阶层高度约为430 cm，长度约为17.7 m，从而位移量远小于看台结构，所以看台受到的最大应力和发生的最大位移，与看台整体的选材以及实际尺寸相比较，均满足使用要求。
4) 本设计与其他国内外看台相关的研究设计相比也存在着很多的不足，首先由于能力上的有限，本看台的设计没有过多地考虑看台的抗风性，更多的是对看台整体结构的设计；看台的倾角对看台的抗风性、安全性、视线合理性均有影响，但是由于缺少相关分析的研究，所以并未深入探究；另外对于看台整体的一个极限载荷情况并没有深入考虑与研究，后期需要对看台整体进行振动分析。所以，虽然本次看台已经达到使用要求，但是仍然需要进一步的优化改进。