1. 引言
电网安全稳定运行是全社会生产作业的重要保障,电力公司的首要任务是确保能够提供稳定、安全的电力 [1] 。近年来,以云计算、大数据、移动互联网、物联网、智能计算为代表的新兴信息通信技术促进各个行业生产、运营方式和模式发生变化,国家电网公司在数字化潮流中也一直走在时代前列,随着大数据中台、云平台等基础设施的完善,目前已经积累了海量的用户数据,能通过海量电力数据的充分挖掘,识别用户的用电模式特点,可以针对不同用电模式的电力用户制定具有针对性的能效管理策略和负荷模式优化方案,有效缓解电网压力 [2] 、支撑有序用电安排等工作的开展;可以为负荷预测、需求响应策略制定以及节能减排工作优化等提供数据支撑 [3] ;也可以提升电网的运行可靠性,促进电网的精细化管理 [4] 。传统的用电模式分析方法主要是按照电力客户的所属行业进行分析 [5] ,该方法需要对各个行业下的用户进行细化分类,随后以定性或定量的方法对用户的用电模式进行具体分析:通过分析不同行业用户的负荷特征可以得出各个行业用电负荷伴随时间的变化规律。随着大数据、人工智能的发展,越来越多的方法被应用到用电模式分析领域。李培强等提出基于模糊聚类原理提出了模糊C均值算法和模糊等价关系两种算法对变电站的综合负荷进行分类的方法 [6] ,Chunlin Zhong等提出使用K-Means算法对用户添加标签,通过用户画像为电力公司了解用户的电力消耗习惯、了解用户需求、提高服务质量提供数据,支撑公司业务发展 [7] ,卜祥国、Wang等通过K-Means算法对家庭月用电量数据进行了家庭用电模式的挖掘与分析,并基于分析结果进行用电量预测应用 [8] [9] ,王建元等人通过DPeaks算法对用户用电数据进行了聚类,并利用聚类结果进行异常用电模式的判定 [10] 。上述算法在各自领域都取得了良好的效果,但时间序列聚类问题的本质实际上是趋势聚类,而传统的聚类算法评价都是通过距离来评价样本间的一致性,而忽略了样本特征间的时序关系。
综上所述,为了解决传统的聚类算法在用电模式聚类时不能有效利用用电时序特征的问题,本文提出了一种基于K-Means改良的PK-Means算法,通过皮尔逊相关系数度量样本间的相似性,有效利用了待聚类样本的时序特征,并在用电模式聚类领域取得了良好的效果。
2. PK-Means算法
2.1. K-Means算法原理
K-Means是数据挖掘领域最常用的无监督聚类算法,主要思想是基于给定的样本集,按照样本之间的距离大小,将样本集划分为K个类,目标是让类内的点尽量紧密的连在一起,而让类间的距离尽量的大。假设K个类为
,优化目标是最小化平方误差和(SSE, Sum of Squares due to Error),其数据表达式如下:
(1)
其中
是类
的均值向量,也称为质心。
K-Means用于聚类分析时的一般步骤如下:
1) 设置要聚类的数量为K,程序最大迭代次数为N。
2) 从给定的数据集中随机选择k个样本作为初始的k个质心向量:
。
3) 计算其他样本到每个质心的欧式距离:
,并将当前样本划分到距离最小的类中。
4) 更新质心数据
(2)
5) 重复上述3)、4)过程直到质心不在变化或者程序达到最大迭代次数。
2.2. 皮尔逊相关系数
皮尔逊相关系数(Pearson Correlation Coefficient),又称皮尔逊积矩相关系数(Pearson Product-Moment Correlation Coefficient,简称PPMCC或PCCs),是用于度量两个变量X和Y之间的相关性,其值介于−1与1之间 [11] 。其定义如下:
(3)
在进行用电模式分析时,通过皮尔逊相关系数可以判断两个个体在用电模式上的相关性,其值越接近1,说明两个个体的用电模式越接近;其值越接近−1,说明两个个体的用电模式差异越大。
2.3. PK-Means算法
基于K-Means算法应用在用电模式分析时存在不能度量时序信息的问题,本文提出一种基于相似度的K-Means聚类算法,因为所采用的相似度度量为皮尔逊相关系数,所以称之为PK-Means算法。PK-Means通过用皮尔逊相关系数替代传统K-Means中的欧式距离作为距离度量,在聚类时充分考虑了用电时序特征,弥补了K-Means在用电模式分析应用方面的缺陷,并取得了较好的聚类效果。
如图1所示,PK-Means的算法执行步骤如下:
步骤1:设置初始化参数,聚类数量为K,最大迭代次数为N;
步骤2:初始化第一个质心,先随机选取一个样本作为第一个质心;
步骤3:初始化其他质心,遍历不属于质心的样本,计算每个样本与当前所有质心的皮尔逊相关系数之和
,选取
最小的样本作为新的质心,重复上述操作直到质心数据等于K;
步骤4:样本类别划分,遍历所有样本,计算当前样本到每个质心的皮尔逊相关系数
,并将当前样本划分到
最大的质心中;
步骤5:质心更新,遍历所有质心,计算当前质心类别下所有样本的均值向量作为新的质心;
步骤6:重复步骤4、步骤5,直到质心不在发生变化或者达到最大迭代次数。

Figure 1. PK-Means algorithm flow chart
图1. PK-Means算法流程图
3. 实验分析
3.1. 数据集
本实验所采用的数据集为上海市某地区146家企业在2022年1~12月每个月的用电数据,该数据由3列构成,分别是户号、月份、用电量,无空值和异常值。
数据集预处理包括转置和数据标准化。如下所示:通过对月份进行转置得到用电时序矩阵,每一行代表了一个用户在2022年12个月的用电时序数据。
(4)
因为每个样本的用电体量都不一样,为了方便用电模式的聚类结果可视化,本实验还对每个用电时序数据做了数据标准化,通过下式将用电量映射到0~1之间。
(5)
3.2. 评价标准
在传统的聚类算法中常用SSE作为聚类效果的评价指标,在类别数量一定时,SSE越小,聚类的效果越好,但在时间序列聚类中用SSE作为评价指标时也存在忽略样本时序关系的问题,基于此本文提出了一种基于SSE改良的聚类评价指标CS (Cumulative Similarity),即累计相似度:其计算方法如下:
(6)
其中
是类
的均值向量,在类别数量一定时,CS越高,聚类的效果越好。
除了CS之外,本文还会通过对聚类结果的可视化来评价聚类效果。
3.3. 实验结果分析
本实验中,分别设置了3、4、5、6、7个聚类数量,记录了CS随迭代次数的变化数据,并对K-Means和PK-Means算法的聚类效果进行对比分析,结果如表1所示,在不同的聚类数量下,PK-Means算法的CS值都要大于K-Means,说明PK-Means在时间序列数据上的聚类表现要优于K-Means。

Table 1. CS table under different K values
表1. 不同K值下的CS表
如图2所示,当K = 4时,CS的增长相对比较明显,后续随着K值增大,CS值的增长相对平缓,聚类数量带来的CS提升收益并不明显,所以选择K = 4作为最终的聚类数量。
如表2所示,第1次迭代时,K-Means算法的CS值要大于PK-Means,但等到第三次迭代时,PK-Means算法的CS值实现了反超,说明PK-Means可以提取到时序特征信息,而K-Means算法的CS值几乎是不变的,进一步证明了K-Means在时间序列聚类中的缺陷。

Table 2. CS table under different iterations
表2. 不同迭代次数下的CS表
如图3所示,在样本特征不复杂的情况下,K-Means与PK-Means的聚类结果非常接近(如类别1、类别2、类别4),但如K-Means算法聚类结果类别2红框内所示,在K-Means的聚类结果中,往往会出现与当前类别的趋势不一致的样本,这些样本在趋势上是不应该划分到类别2的,属于误分类的样本,PK-Means的表现整体来说比K-Means更稳定,在用电模式分析时,我们需要样本在时间趋势上保持一致的聚类效果,所以从可视化的结果来看PK-Means也是优于K-Means的。
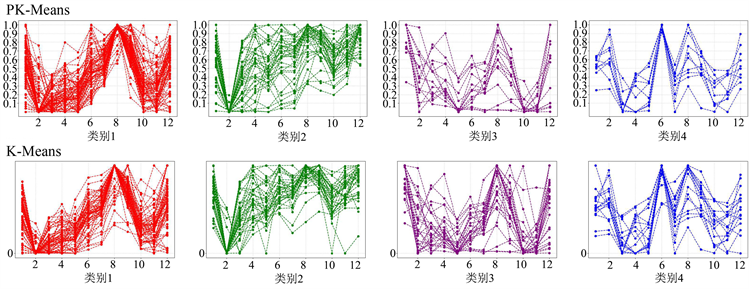
Figure 3. Visualization of clustering results
图3. 聚类结果可视化
4. 结论
本文提出了一种基于K-Means改进的PK-Means算法,用于用电模式的聚类分析,通过皮尔逊相关系数来度量个体之间用户模式的一致性,解决了传统K-Means算法在时序数据聚类方面不能有效利用时序信息的缺陷,并使用累计相似度(CS)对聚类效果进行度量,通过上海某地区的真实用电数据验证了本文所提方法的有效性,在用电模式聚类场景下取得了更好的聚类效果,为电网精细化管理,用电策略规划等管理政策提供了数据支撑。