1. 引言
我国拥有广阔的大陆架海域,其中离岸20海里内小于30 m深的水域占80%以上。随着经济全球化和“一带一路”的不断推进,港口运输、海底隧道、跨海大桥、环境、资源勘查等工程项目建设也将随之增加。同时近年洪涝灾害发生频繁,严重威胁我国人民生命财产安全和社会稳定。因此准确有效探测陆上湖泊、河流等水体环境和近海浅水域水下地层结构信息具有重要意义。
瞬变电磁法(TEM)作为一种重要的地球物理探测方法,具有查明地层电阻率空间分布的能力,在矿产资源勘查和油气勘探中应用广泛,并逐渐拓展到军事、环境、工程等领域 [1] ,其中水域勘探是瞬变电磁法应用领域的一个重要分支。在浅水环境中,相较于频率域电磁法,瞬变电磁法可以有效分离空气波信号和水底地层响应 [2] [3] [4] ,对低阻体具有更高的分辨率 [5] ,并且在利用瞬变电磁法进行浅水域探测时还可使用更为简便的表面拖曳系统,具有更高的工作效率 [6] [7] ,因而瞬变电磁法在浅水域探测中受到越来越多的关注。目前浅水域瞬变电磁探测多采用水下观测方式,将装置置于水下,受水流扰动影响,造成工作时定位困难、定位精度低,并且对仪器的密封性和防水性要求较高。此外,将天线装置置于水下时不再是地面上的半空间环境,也不是深水域中的全空间环境,此时涡流场传播规律较为复杂。同时,由于湖泊、河流和近海水域水深较浅以及大尺寸线圈装置瞬变电磁早期响应形态较为复杂、解释难度较大等因素,大尺寸线圈不宜用于水域瞬变电磁勘探,通常采用小回线装置 [8] 。理论上相同时间内电磁场扩散深度与回线尺寸无关 [9] ,瞬变电磁法探测深度主要由观测时间决定,小回线装置瞬变电磁若观测时间足够长同样可探测到较大深度,但受仪器实际观测精度等限制,探测深度有限。为提高探测深度,势必需要增加收发线圈匝数和增大发射电流,进而造成收发线圈互感严重,早期信号衰减缓慢,形成一个较宽的平台,导致早期信息丢失严重,形成较大的浅层探测盲区,对浅水域探测极其不利,压制与消除收发线圈的互感已成为小回路瞬变电磁法的关键问题之一。基于此,席振铢等 [10] 提出等值反磁通瞬变电磁法(OCTEM),通过建立双线圈源的一次场零磁通面,在零磁通面上接收不受一次场对接收线圈影响的纯二次场响应,通过理论推导、数值计算和实测试验证明了该方法对压制互感、减小探测盲区的有效性。表面拖曳式等值反磁通瞬变电磁法有望弥补常规瞬变电磁法在浅水域探测中的上述诸多不足。
目前,瞬变电磁数据资料解释主要通过一维反演获得电阻率分布 [11] ,但通过一维反演结果拼接成拟二维剖面通常会产生电阻率突变,使得在复杂地质条件下一维反演难以得到准确的地下结构信息 [12] 。三维反演是提高瞬变电磁解释精准度的重要方法,正演作为反演的基础,准确有效的瞬变电磁三维正演算法有利于提高浅水域瞬变电磁三维反演成像和资料解释水平,因此越来越多的学者致力于浅水域瞬变电磁法正演模拟研究之中。Avdeeva等 [13] 通过三维时域有限差分法计算并分析了不同海水深度、储层深度、厚度及电阻率参数下瞬变电磁响应规律。李予国等 [6] [7] 完成了浅水区瞬变电磁法一维数值模拟,研究了不同海水深度下空气波对瞬变电磁响应的影响,结果表明:空气波到达时间主要受海水深度影响,相较于深水域,浅水域瞬变电磁探测可使用更为简便的表面拖曳系统。赵越等 [14] [15] [16] 通过矢量有限元法对浅海小型低阻体和浅海掩埋未爆物进行了中心回线装置瞬变电磁三维正演模拟,进一步研究了中心回线瞬变电磁法对海底的探测能力。邓宇 [17] 通过时域有限单元法进行了浅水域小规模低阻异常体三维正演模拟,研究了浅水区低阻体瞬变电磁响应规律。Ji等 [18] 基于虚拟波场和扩散波场的对应原理,在虚拟波场中求解麦克斯韦方程组,利用FDTD实现了浅水域瞬变电磁三维数值模拟,并讨论了空气和海水深度等参数对瞬变电磁响应的影响。Xu等 [19] 利用FDTD模拟计算了浅水域典型低阻异常体模型瞬变电磁响应,研究了浅水层厚度和电阻率等参数对浅水域小回路瞬变电磁响应的影响。目前浅水域瞬变电磁数值模拟仍以常规瞬变电磁法为主,关于等值反磁通瞬变电磁法数值模拟还鲜有研究,且集中在地面上 [20] [21] [22] ,开展浅水域等值反磁通瞬变电磁法三维数值模拟研究十分必要。
本文首先基于水面等值反磁通瞬变电磁探测的基本理论,采用矢量有限元法完成了浅水域等值反磁通瞬变电磁法三维正演模拟,然后分析了不同参数对等值反磁通瞬变电磁响应的影响,最后建立典型浅水域地电模型,采用矢量有限元法模拟计算等值反磁通瞬变电磁响应,并总结和分析其响应特征与规律。
2. 水面等值反磁通瞬变电磁法三维正演理论
2.1. 水面等值反磁通瞬变电磁法基本原理
水面等值反磁通瞬变电磁法原理与传统瞬变电磁法相同,但装置有所不同 [23] ,浅水域拖曳式等值反磁通瞬变电磁探测原理与装置示意图如图1所示,其采用两个完全相同且上下平行共轴的线圈充当反向对偶磁源发射一次场,在反向对偶磁源的正中间平面上一次场磁通量始终为零,在一次场关断间隙于该平面用接收线圈测量纯二次场响应,从而达到消除探测盲区的目的。
浅水域水面等值反磁通瞬变电磁法采用中心回线装置观测,仅用感应线圈观测垂向磁场分量,水面等值反磁通瞬变电磁法二次磁场时间导数
晚期响应可用下式表示:
(1)
其中I为发射电流大小;d为反向对偶磁源间距;
为电导率;a为发射线圈半径;
为磁导率;C为待定常数;t为衰减时间。
常规中心回线装置瞬变电磁法均匀半空间响应晚期表达式为:
(2)
由上述表达式可看出,在均匀半空间中,等值反磁通瞬变电磁法
响应幅值与发射磁矩、大地电导率平方和反向对偶磁源间距成正比关系,常规中心回线装置瞬变电磁法
响应幅值与电导率成3/2次方关系,因此相较于常规水面瞬变电磁法,水面等值反磁通瞬变电磁法对电阻率变化具有更高的灵敏度和分辨能力。
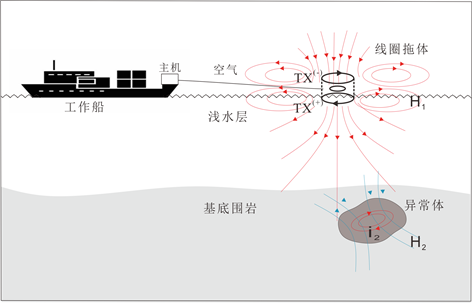
Figure 1. Principle and device diagram of towed opposing coils transient electromagnetic detection in shallow water
图1. 浅水域拖曳式等值反磁通瞬变电磁探测原理与装置示意图
2.2. 矢量有限元法正演原理
瞬变电磁三维数值模拟方法主要包括积分方程法(TDIE)、有限元法(FEM)、有限差分法(FDTD)和时域伪谱方法(PSTD)等。相较于有限差分法、积分方程法等数值模拟方法,有限元法网格剖分自由,可更好模拟地形起伏及复杂地电模型,近年来在电磁法数值模拟中广泛应用。有限元法包括矢量有限元法(Vector Finite Element Method)和节点有限元法(Node-Based Finite Element Method)。节点有限元法将自由度赋于节点,需要进行散度校正才能避免出现伪解现象。矢量有限元法使用矢量基函数近似代替未知函数,将自由度赋于棱边,避免了节点有限元法需要进行散度校正问题。同时,矢量有限元法可以更好地处理介质及电性体的边界条件 [24] [25] 。因此本文采用矢量有限元法对浅水域等值反磁通瞬变电磁法三维模型响应进行数值模拟。
2.2.1. 控制方程及边值问题
忽略位移电流作准静态近似时无源介质中Maxwell方程组为:
(3)
(4)
(5)
(6)
式中,E为电场强度,
为磁导率,H为磁场强度,
为电导率,Js为外加源电流密度。取时间因子
,
为角频率,则(1)式可表示为:
(7)
对(5)式左右两端同时取旋度得:
(8)
将(2)式代入(6)中得到基于电场的矢量波动方程:
(9)
上式中的电场
为电场总场,由一次电场和二次电场组成。若直接对总场进行求解,由于场源空间奇异性问题,在对计算区域进行网格剖分时需在场源附近作加密处理,将导致计算量增加。为此,本文通过求解二次电场解决上述问题。将总场
分解为一次电场
和二次电场
,由于等值反磁通瞬变电磁法采用上下等值反向的双线圈源,将双线圈源分为上源(命名为Up)和下源(命名为Down),通过矢量叠加原理,则有:
(10)
(11)
将(8)代入(7)中,电场矢量波动方程分解整理后可得:
(12)
(13)
(14)
(15)
式中
代表电导率异常。对于不同介质分界面,电场强度
切向分量连续,满足:
(16)
代表介质分界面单位法向矢量,
和
代表界面两侧二次电场。在无穷远边界上,电场满足齐次Dirichlet边界条件:
(17)
2.2.2. 矢量有限元分析
本文使用六面体矩形单元对计算区域进行网格剖分,矩形单元及棱边局部编号规则如图2所示。
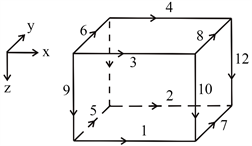
Figure 2. Schematic diagram of the local numbering rules for rectangular elements and edges
图2. 矩形单元及各棱边局部编号规则示意图
将计算区域通过矩形单元剖分方式剖分为N个矩形单元,共Ns节点。在矩形块棱边元的第i条边上赋一个不变的切向场向量
,其中i取1到12,由矩形单元矢量基函数表达式 [26] ,单个矩形块棱边元内二次电场
可表示为:
(18)
由于单个矢量基函数具有散度为零的性质,即有:
(19)
则式(13)表示的二次电场有:
(20)
即二次电场在棱边元中自动满足零散度条件,避免计算过程中出现伪解。
本文采用Galerkin法推导有限元方程组 [26] [27] ,式(10)表示的二次电场矢量波动方程的残数R及单个矩形单元e的残数Re分别为:
(21)
(22)
将(13)式代入(17)式,并用Galerkin法对各矩形块棱边元内残数
加权积分:
(23)
式中Ve为单元e的积分区域,i、j为单元棱边编号。令与每一矩形单元棱边相关的残数Re进行加权积分后为零,并进一步改写为方程组形式为:
(24)
其中:
,
.
对所剖分的网格进行单元分析后,得到大型线性稀疏方程组,该类方程组的求解主要包括直接法和迭代法两种方式。相较于直接法,迭代法占用内存小,计算速度快,本文采用共轭梯度法进行求解。求解方程组(24)得到频率域内二次电场,通过法拉第定律求得频率域内二次磁场
,其中:
(25)
随后需将求得的二次磁场通过时频转换计算其时间域响应。常用的时频转换方法有G-S变换、傅立叶反变换、余弦变换等,基于本文正演模型,选择余弦变换方法。计算公式如下:
(26)
由于采用瞬变电磁法进行野外工作时测量的参数通常为感应电动势,因而通过法拉第电磁感应定律
,将求得的电场响应转换为感应电动势。
3. 算法验证及模型分析
3.1. 算法正确性验证
为验证本文三维矢量有限元算法的正确性与计算精度,将本文三维矢量有限元计算结果与一维数值滤波解进行对比。所采用的模型参数如下:发射线圈面积为4 m2,发射电流为20 A,发射波形为上升沿和下降沿时间皆为0.2 ms、稳定时间为4 ms的梯形波,反向对偶磁源间距为1 m,接收线圈等效面积为100 m2,下发射线圈位于水面上;空气电阻率为106 Ω∙m,为便于计算分析,将基底围岩简化为均匀介质,电阻率为100 Ω∙m;由于海水电阻率一般取0.33 Ω∙m,陆上河流、湖泊水电阻率为20 Ω∙m左右,为不失一般性,此处水的电阻率取10 Ω∙m,浅水域水深较浅,通常为十几到30米之间,此处水深设为20 m。计算结果如图3所示,结果表明二者最大相对误差控制在6%以内,整体误差保持在3%左右,吻合情况较好,说明本文算法正确、计算精度较高。
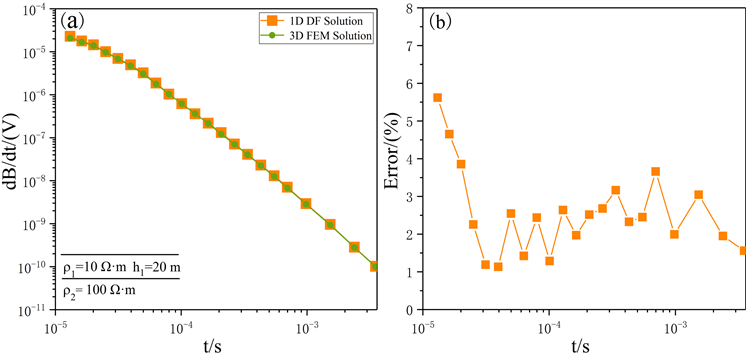
Figure 3. Comparison of 3D vector finite element calculation results with 1D numerical filtering solutions. (a) Response curve; (b) Relative error
图3. 三维矢量有限元计算结果与一维数值滤波解对比图。(a) 响应曲线;(b) 相对误差
3.2. 不同参数下OCTEM响应规律
为研究不同水深和不同沉积层电阻率下等值反磁通瞬变电磁响应响应规律,以上述算法验证模型为例,利用本文算法计算了20 m、50 m、100 m、500 m水深条件下等值反磁通瞬变电磁响应及50 m水深条件下沉积层电阻率分别为1、10、100和1000 Ω·m时等值反磁通瞬变电磁响应,计算结果如图4所示。
图4表明,在使用表面拖曳装置时,等值反磁通瞬变电磁早延时响应主要反映浅水层,晚延时响应主要反映基底围岩。不同水深情况下衰减曲线形态早期基本重合,水深变化影响主要体现在衰减曲线相对晚期形态。浅水环境下稍晚延时的等值反磁通瞬变电磁响应要小于深水环境下响应,随着水深增加,晚期响应幅值增大,并逐渐接近更大水深条件下响应幅值。不同基底围岩电阻率条件下,等值反磁通瞬变电磁法对基底围岩电阻率变化反映灵敏,不同电阻率基底围岩下等值反磁通瞬变电磁响应幅值差异明显,低阻基底围岩响应幅值远大于高阻基底围岩响应幅值,表明该方法容易穿透高阻层,探测到低阻层。可根据等值反磁通瞬变电磁响应计算水体深度、基底围岩电阻率。
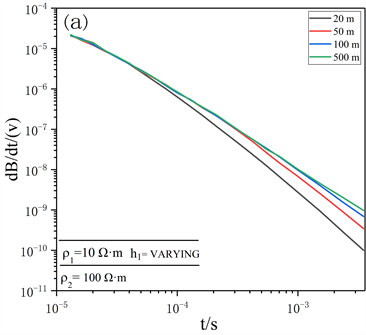
Figure 4. Opposing coils transient electromagnetic response curves under different parameters. (a) Different water depths; (b) Different basement surrounding rock resistivities
图4. 不同参数条件下等值反磁通瞬变电磁响应曲线。(a) 不同水深;(b) 不同基底围岩电阻率
4. 三维算例
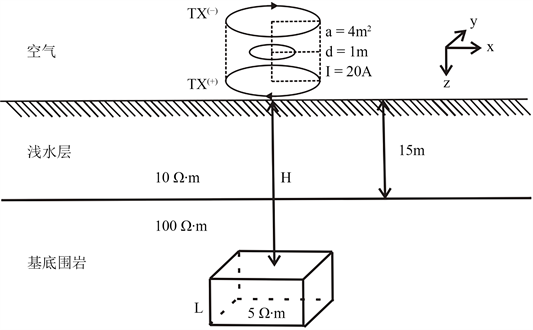
Figure 5. Schematic diagram of 3D anomalous body model in shallow water
图5. 浅水域三维异常体模型示意图
为研究等值反磁通瞬变电磁法对浅水域低阻体的探测能力,建立如图5所示浅水域异常体模型并采用矢量有限元法进行三维正演计算,其中反向对偶磁源发射线圈面积为4 m2,间距为1 m,接收线圈位于与反向对偶磁源正中间的零磁通面上,有效接收面积为100 m2,发射波形为上升沿和下降沿时间皆为0.2 ms、稳定时间为4 ms的梯形波,电流大小为20 A;水的电阻率为10 Ω∙m,水深为15 m,基底围岩电阻率为100 Ω∙m;瞬变电磁法对低阻体敏感,对高阻体的分辨能力远小于低阻体,因此等值反磁通瞬变电磁法多用于探测浅部低阻地质体,异常体埋深30 m,电阻率为5 Ω∙m,尺寸为60 m × 60 m × 40 m。采用非均匀网格对计算区域进行网格剖分,在异常体和发射源附件进行网格加密处理以提高计算精度,网格数为65 × 65 × 61,最小剖分网格大小为5 m × 5 m × 5 m。剖面范围为−150 m~150 m,其中−150 m~−30 m与30 m~150 m范围内线距和点距为30 m,在异常体正上方范围内进行加密,−30 m~30 m范围内线距和点距为15 m,主测线位于异常体中心正上方,共设计13条测线,每条测线13个测点,共169个测点,在内存为16 GB、处理器为11,800 H的个人计算机上所有计算测点共耗费86,359 s,平均每个测点计算时间为511 s。
图6为主测线等值反磁通瞬变电磁响应多测道剖面图,为更加清晰直观地分析浅水域等值反磁通瞬变电磁响应特征与规律,取多个不同时间道的响应幅值绘制三维等值反磁通瞬变电磁响应图,如图7 (x,y方向坐标轴为线性坐标,z方向坐标轴为对数坐标)所示,其中图7(a)、图7(b)和图7(c)分别为t = 0.129 ms、t = 0.337 ms和t = 1.73 ms时间道响应值。从图6、图7可以看出,异常体以外区域等值反磁通瞬变电磁响应幅值低且平缓,变化较小;异常体内部响应幅值陡然增大,异常清晰,与异常体以外区域对比明显,较好地反映了异常体形态,说明等值反磁通瞬变电磁法可以有效探测浅水域低阻异常体,对低阻异常体具有较高的探测与分辨能力。
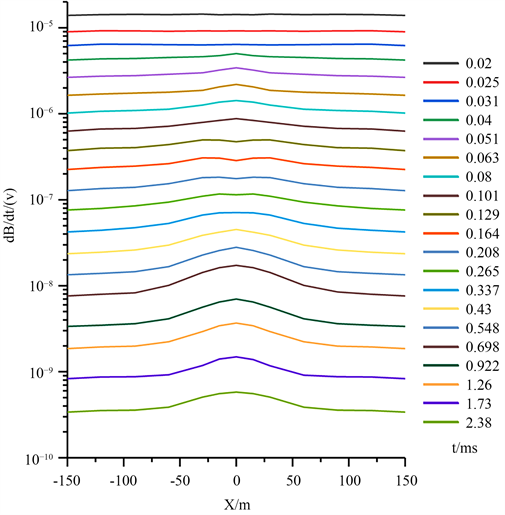
Figure 6. Main measurement line opposing coils transient electromagnetic response multi-channel profile
图6. 主测线等值反磁通瞬变电磁响应多测道剖面图
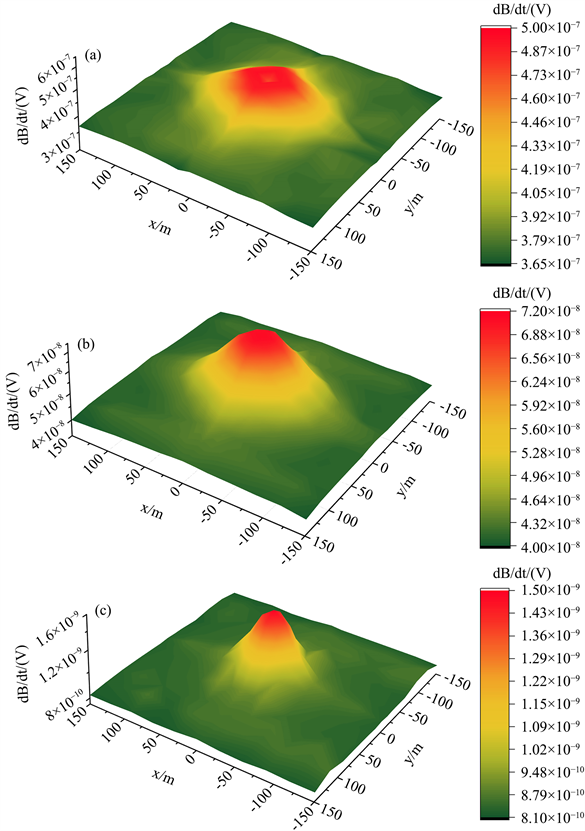
Figure 7. Numerical simulation of the opposing coils transient electromagnetic three-dimensional response. (a) 0.129 ms; (b) 0.337 ms; (c) 1.73 ms
图7. 数值模拟等值反磁通瞬变电磁三维响应。(a) 0.129 ms;(b) 0.337 ms;(c) 1.73 ms
5. 结论
本文基于矢量有限元法,建立典型浅水域低阻异常体模型,采用反向对偶磁源,首次实现了浅水域等值反磁通瞬变电磁法的三维正演模拟,并得到以下结论:
1) 通过与典型浅水域地电模型数值滤波解进行对比,证明采用矢量有限元法求解浅水域等值反磁通瞬变电磁响应切实有效,且算法简单、精度较高;
2) 浅水层可视为低阻覆盖层,瞬变电磁法存在低阻屏蔽现象,对低阻覆盖层下的异常体响应较为微弱。等值反磁通瞬变电磁法对浅水域低阻异常体响应强烈,异常清晰明显,能较好地确定异常体边界,具有较强的探测能力。
NOTES
*通讯作者。