1. 引言
磁流变液减振器因其耗能较低、阻尼响应迅速、阻尼调校空间大且实时可控等诸多优点已成为减振器的重要发展方向之一,如今,磁流变技术已被广泛应用于房屋桥梁减振、直升机起落架、汽车减振器以及假肢膝关节等器件上 [1] [2] [3] [4] 。然而,在Gomez-Ramirez等 [5] 的研究工作中发现,由于磁流变液中铁磁颗粒与基载液之间存在巨大的密度差,导致铁磁颗粒极易产生沉降现象致使磁流变液减振器控制特性劣化,大大降低了减振器的使用寿命。
于是,一种新型的磁流变材料——磁流变脂应孕而生 [6] 。磁流变脂以润滑脂为基载液,润滑脂皂纤维结构能够有效防止铁磁颗粒发生沉降,使其在改善磁流体沉降稳定性方面表现出了得天独厚的优势 [7] [8] 。但是磁流变脂却因其初始粘度高,流动性差,屈服应力可调性不够高 [9] 的缺点受到了发展限制。因此,对磁流变脂减振器进行结构设计,以此降低其初始阻尼力、提高阻尼可调范围很有必要 [10] [11] 。
本文的主要研究内容是通过对磁流变脂减振器进行结构设计以改善其原有缺点,并基于宾汉本构模型,建立减振器输出阻尼力数学模型,并对减振器原有结构参数进行多目标优化设计,最后在MATLAB环境下对优化前后模型进行仿真分析并进行对比,为磁流变脂减振器的合理设计提供理论参考。
2. 结构设计
本文所设计的位移相关磁流变脂减振器的结构示意图如图1所示,为解决磁流变脂初始粘度大、流动性差、阻尼可调范围不够高的缺点,在该减振器的缸筒静平衡位置加工了一圈泄流环槽;并在活塞头处开有两个与环形阻尼通道并联的旁通孔,以及两侧端盖与其配对的4根堵杆。通过泄流槽与旁通孔的共同作用以减弱减振器初始状态下诸多缺点所带来的影响,同时实现减振器输出阻尼力随着活塞位移的变化而变化,并根据活塞到达的不同区域将减振器划分为“软”、“硬”、“过渡”及“中间”四段阻尼区。汽车在空载状态下,活塞在泄流槽软阻尼区内振动,减振器的阻尼力较低有利于改善目标车的乘坐舒适性;车辆满载状态下,活塞在中间阻尼区振动,提供较大阻尼力,保证了目标车的操纵稳定性;当遇到紧急状况时(如急转弯),活塞运动幅度较大以致到达硬阻尼区,减振器输出阻尼力达到最大,车辆行驶安全性提高。

Figure 1. 3-D drawing of the displacement-dependent magneto-rheological grease damper
图1. 位移相关磁流变脂减振器三维模型图
3. 动力学模型
磁流变脂在无外加磁场时,表现为牛顿流体的性质;当施加外部磁场时,磁流变脂表现为宾汉流体,宾汉流体本构模型可用下式近似描述:
(1)
式中:dv/dz为剪切应变率;τ为剪切应力;
为与磁场强度相关的剪切屈服应力;η为磁流变脂粘度。
图2所表示为位移相关磁流变脂减振器结构示意图,从图中可以看出,磁流变减振器通过活塞头的位移使腔室1,2产生压差迫使磁流变流体流经阻尼通道,以此来控制的输出阻尼力的大小。当减振器活塞头处于软阻尼区工作时,阻尼通道内流场与环形泄流槽和旁通孔内流场共同构成活塞头内部流场,因此必须分别对三者进行分析。
3.1. 环形阻尼通道内流场分析
因环形阻尼通道半径远大于其宽度,故在分析阻尼通道内流场时可将其简化为平板模型,以阻尼通道间隙中点为坐标原点,垂直与磁流变脂流动方向建立坐标系。基于平板模型理论,流体在磁场作用下流速分布如图3所示。其中区域I为屈服区,II区为非屈服区。
平板模型的流体力学方程为:
(2)
式中:
为平板模型两端压力差;L为阻尼通道有效长度;A为平行平板之间的流动边界常数。
由对称性可知当
时,
,求得式(2)中流动边界常数
,结合式(1)得到I区的速率表达式为:
(3)
II区是非屈服区,其速率变化与z无关,故当
时求得非屈服区的厚度大小
为:
(4)
式中:l为阻尼通道中磁力线穿过的有效长度。
故II区的速率表达式为:
(5)
根据阻尼通道内磁流变脂两部分的运动速度,可得流经环形阻尼通道的流量
为:
(6)
式中:
为内导磁环半径。
对上式进行化简,并求解,得:
(7)
3.2. 旁通孔内流场分析
旁通孔处于活塞头内部,小孔内无作用磁场,所以旁通孔内的磁流变脂依旧为牛顿流体,根据流体力学Hagen-Poiseuille定理可以得出流过旁通孔的流量
为:
(8)
式中:n为旁通孔个数,d为旁通孔直径,
为旁通孔两端压力差。
3.3. 环形泄流槽内流场分析
环形泄流槽在外筒和活塞总成之间,由于外筒为不导磁的不锈钢材质,磁感线无法穿过环形泄流槽,即在环形泄流槽内磁流变脂不受磁场控制,为牛顿流体。可将环形泄流槽视为圆柱环形缝隙流动,基于平板模型理论可得流经环形泄流槽流量
为:
(9)
式中:
为外导磁环半径,
为环形泄流槽宽度,
为环形泄流槽两端压力差。
3.4. 总输出阻尼力
由于阻尼通道、旁通孔与环形泄流槽是相互并联的,所以可以得到:
(10)
当活塞头以
的速度运动时,可以得到流经活塞头的总流量Q为:
(11)
式中:
为活塞有效面积;
,
为活塞面积;
为活塞杆面积。
由此可以得到活塞头两端压差
与活塞头运动速度
之间的关系,进而由
得到活塞头在软阻尼区工作时的输出阻尼力
的表达式为:
(12)
同理可得该减振器在不同阻尼区内的输出阻尼力F为:
(13)
式中:x为活塞头位移。
4. 结构参数优化设计
4.1. 尺寸结构优化方案
结构设计大多为重复迭代的过程,可以通过仿真方法进行迭代,以此来节约结构设计的研发时间和成本。而磁流变减振器的性能指标由多个结构参数共同决定,因此非常适合多目标优化的方式对减振器结构参数进行选择来提高设计效率。本文利用多目标优化软件modeFRONTIER强大的CAE流程自动化及软件集成平台,与数值计算软件MATLAB相结合,采用modeFRONTIER自身集成的优化算法搭建磁流变减振器多目标优化模型进行多目标优化设计。
本文目标函数为第3节中得到输出阻尼力数学模型,以位移相关磁流变脂减振器软阻尼区最小阻尼力和硬阻尼区最大阻尼力为优化目标;将主要结构尺寸参数作为优化变量,并设定优化范围,具体如表1所示;为各个阻尼区阻尼力大小设置约束条件,具体如表2所示。

Table 1. Optimized variables and variable ranges
表1. 优化变量及变量范围
4.2. 优化结果
由多目标优化软件modeFRONTIER结合MATLAB所搭建的位移相关磁流变脂减振器优化模型如图4所示。根据所设计的优化目标随机设定500组初始优化变量,选择基于遗传算法的多目标优化算法——NSGA-II,其中将交叉概率设置为0.9,遗传代数设置为100代。
图5所示为Pareto解集,其中黄色点为随机变量组中不满足要求的解,绿色点为满足要求的解,剔除不满足要求的黄色点后便得到了图6。在一定的约束条件下,提高减振器最大阻尼力和降低最小阻尼力是相互矛盾的,因此需要根据实际和设计要求确定最优解,而本文优先考虑了减振器的最小输出阻尼力,所以选择的优化结果如表3所示。
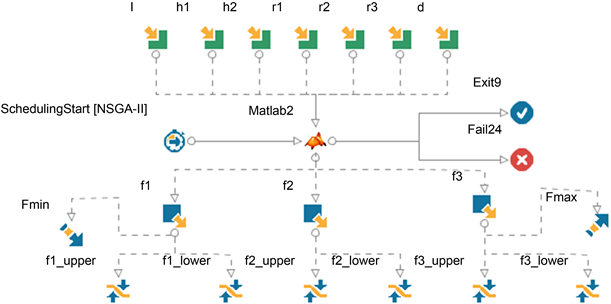
Figure 4. The multi-objective optimization model of the damper
图4. 减振器多目标优化模型
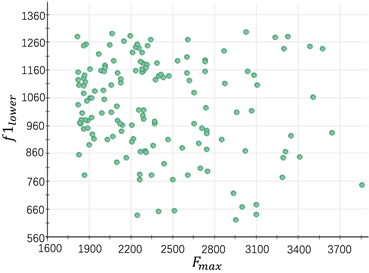
Figure 6. The Pareto solution set that satisfies the requirements
图6. 满足要求的Pareto解集
4.3. 仿真及优化结果分析
图7所示为活塞速度为0.251 m/s,振幅为30 mm情况下,通入五种电流(即0 A、0.5 A、1 A、1.5 A、2 A)优化前减振器输出阻尼力和活塞位移的关系图。如图所示,该减振器阻尼力随着电流的增大而增大,即是表示其具有明显的磁流变效应,可达到连续可控的效果。在无外加电流的情况下,该减振器软阻尼区输出阻尼力为135.1 N,硬阻尼区输出阻尼力为236.7 N,降阻率μ为42.92%;在通入2 A电流的情况下,该磁流变脂减振器硬阻尼区的输出阻尼力为2051.9 N,与原始磁流变脂减振器相比阻尼可调范围K从8.67增大到了15.19,验证了该结构的有效性。相同电流下,随活塞位移达到不同阻尼区减振器呈现出不同输出阻尼力,为车辆乘坐提供了更好的舒适性,同时提高了车辆操纵的稳定性和安全性。
其中,降阻率
和阻尼可调范围K的计算公式为:
(14)
(15)
式中:
为现阻尼力,
为原阻尼力,
为最大输出阻尼力,
最小输出阻尼力。
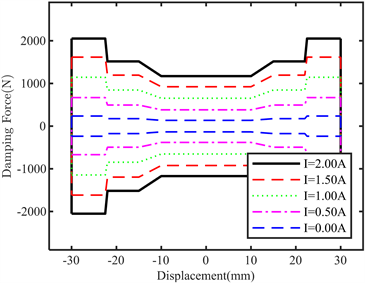
Figure 7. Damping force versus displacement of the damper before optimization
图7. 优化前减振器阻尼力与位移关系
图8所示为活塞速度为0.251 m/s,振幅为30 mm情况下,通入五种电流(即0 A、0.5 A、1 A、1.5 A、2 A)优化后减振器输出阻尼力和活塞位移的关系图。如图所示,在无外加电流的情况下,该减振器软阻尼区输出阻尼力为143.2 N,硬阻尼区输出阻尼力为581.1 N,降阻率μ为75.36%;在通入2 A电流的情况下,该磁流变脂减振器硬阻尼区的输出阻尼力为2997.31 N,阻尼可调范围K从优化前的15.19增大到了20.93。
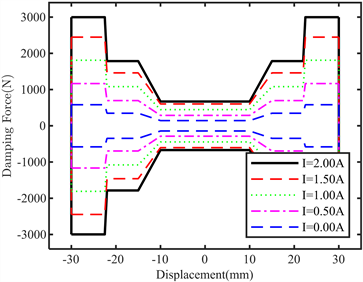
Figure 8. Damping force versus displacement of the damper after optimization
图8. 优化后减振器阻尼力与位移关系
图9所示为活塞速度为0.251 m/s,振幅为30 mm情况下,2 A电流下优化前后减振器输出阻尼力和活塞位移的关系图。2 A电流下各阻尼区阻尼力以及阻尼可调系数如表4所示。可见优化后减振器降阻率和阻尼可调系数均有明显提高,符合优化设计初衷。且优化后减振器输出阻尼力符合我国汽车减振器行业标准。
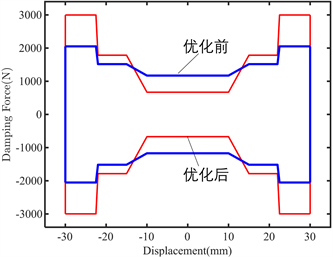
Figure 9. Comparison of damping force and displacement of the damper before and after optimization under 2 A current
图9. 2 A电流下优化前后减振器阻尼力与位移关系对比

Table 4. Comparison before and after optimization
表4. 优化前后对比
5. 结论
针对磁流变液易沉降,不稳定;而磁流变脂减振器初始阻尼力大,阻尼可调范围小的实际问题,本文提出了一种位移相关磁流变脂减振器。基于Bingham模型对该减振器各段阻尼区建立了数学模型,并通过所建立的数学模型,在modeFRONTIER多目标优化软件中,对减振器结构参数进行了多目标优化设计。最后通过MATLAB对优化前后的减振器进行了仿真研究。仿真结果表明,位移相关磁流变脂减振器能有效降低减振器初始阻尼力,且提高了减振器的阻尼可调系数。优化后相较优化前,减振器初始状态降阻率从42.92%提升到了75.36%;阻尼可调系数从15.19提高到了20.93。本文的研究可为磁流变脂减振器的结构设计提供重要方法论指导。