基于HIL仿真平台的电动汽车SOE在线估计研究

Research on the Online Estimation of SOE for Electric Vehicles Based on a Hardware-in-the-Loop (HIL) Simulation Platform

摘要: 本文基于硬件在环(HIL)仿真对电动汽车SOE在线估计进行研究。首先基于dSPACE平台搭建了以锂电池为硬件的HIL仿真平台。然后分析了电动汽车动力电池剩余能量(SOE)的计算方法，并为此在Simulink环境下建立了2阶Thevenin等效电路电池模型和包含汽车动力学模型、驾驶员模型、电机模型三部分的整车模型。接下来借助RTW和RTI软件平台完成编译和代码的转换，将上述Simulink仿真模型作为HIL平台的控制逻辑上传到dSPACE实验系统中。综合以上工作，实现了由HIL平台控制真实锂电池在电动汽车NEDC和WLTP混合工况下作为电池组电芯进行充放电，并实时采集和监控真实电池的电流电压数据。最后基于该HIL仿真平台的在线运行，以均方根误差(RMSE)为评价标准实时地调试优化动态参数模型、算法，完成了对电池SOE在线估计的研究。

Abstract: This paper conducts research on the online estimation of state of energy (SOE) for electric vehicles using hardware-in-the-loop (HIL) simulation. First, a HIL simulation platform with a lithium battery as the hardware was established on the dSPACE platform. Then, the calculation method for the re-maining energy of the electric vehicle power battery (SOE) was analyzed, and a two-order Thevenin equivalent circuit battery model and a vehicle model consisting of three components— vehicle dy-namics, driver model, and motor model—were created in Simulink. Subsequently, the Simulink simulation model was compiled and converted into code using the RTW and RTI software platforms, and uploaded to the dSPACE experimental system as the control logic for the HIL platform. With these steps, the real lithium battery can be controlled by the HIL platform to charge and discharge as battery cells in electric vehicles under the mixed operating conditions of NEDC and WLTP, while real-time current and voltage data are collected and monitored. Finally, based on the real-time op-eration of the HIL simulation platform, the research on online estimation of battery SOE was com-pleted by dynamically optimizing the parameter model and algorithm in real time using root mean square error (RMSE) as the evaluation standard.

1. 引言

近年来，电动汽车行业的快速发展不断推动着电池相关技术的升级和提高。然而，与传统燃油汽车的燃油储量可以直接测量不同，电池内储存的能量是无法直接测量的。此外，电池能量状态受多种因素的影响，因此，估算电动汽车动力电池剩余可放电能量(SOE)的难度相对较大 [1] 。SOE反映了电池的能量状态，它直接影响着电动汽车的剩余续驶里程。由于剩余续驶里程的估计不准确，导致了用户里程焦虑，这已经成为电动汽车推广普及的一个重要障碍。因此，如何精准地估算电池剩余可放电能量已成为电动汽车剩余续驶里程估计的难点和关键。

目前常见的车载电池管理系统(BMS)中，为了减少计算量，大都采用电池荷电状态(SOC)来简单直接地表征剩余可放电能量 [2] 。一般而言，这种方法是根据模糊的经验建立当前电量与剩余能耗(SOE)之间的简单线性关系，能耗预测则通常使用不同长度时间段的历史平均能耗来作为未来能耗预测值 [3] [4] 。然而，这种方法存在一定的缺陷。一方面，虽然该方法简单易行，但它容易高估电池剩余可放电能量，导致对剩余续驶里程的高估，最终造成用户里程焦虑，即实际使用中常见的“虚电”现象。另一方面，无论是简单直接的模糊经验法还是更复杂的仿真建模法，其研究过程都是“电池实验数据”到“根据数据建立经验关系或仿真建模”再到“实车数据验证”的信息单向流动，无法在调整经验关系、调试仿真模型或优化算法时将真实电池的实时状态信号反馈作为参考。

综上所述，为提高剩余可放电能量的估计精度，本文基于dSPACE搭建硬件在环仿真(HIL)平台进行研究。该研究利用实际电池作为在环硬件，并通过与汽车动力学模型、PID驾驶员控制模型、电机模型、电池模型的联合仿真，实现对剩余可放电能量SOE的在线估计的研究。与传统的基于经验关系或仿真建模的方法相比，该方法通过反馈真实电池的实时状态信号进行参考，使得研究过程更加接近实际情况。因此，本研究提供了一种基于HIL平台的电动汽车剩余续驶里程估计方法，该方法在提高估计精度的同时，也能够有效解决现有方法所存在的虚电现象问题，具有一定的研究和应用价值。

2. 硬件在环仿真平台

硬件在环仿真(HIL)的特点在于实际组件与仿真组件之间的实时联合运行，并且可以完全或部分地模拟执行器、物理过程、传感器组成的受控过程 [5] 。本文采用dSPACE平台作为软件控制部分的执行器主要起以下作用：1) 根据对NEDC、WLTC等不同汽车工况下整车联合仿真模型的运行计算能耗、功率，来控制真实电池的充放电；2) 采集真实电池的电压电流数据回传到系统；3) 通过设置的算法估计SOE、能耗，通过与真实能耗数据的实时对比验证调试模型、算法，实现对电池SOE的在线估计研究。

2.1. 本研究中HIL平台的架构原理

基于dSPACE的HIL仿真平台架构原理如图1所示，dSPACE作为整个HIL平台的软件控制端负责控制和协调各个部件之间的工作，同时通过Simulink将联合仿真模型嵌入dSPACE中，代替BMS的数据处理部分实现关于SOE、能耗的估算算法。

运行流程中，整车模型和SOE估计算法在Simulink仿真环境下运行调试成功后，将系统中对应于dSPACE I/O口的Simulink模块接入其中，然后便可借助RTW和RTI软件平台完成编译和代码的转换，生成的.sdf文件通过以太网接口下载到dSPACE实验系统中。此时Simulink仿真电路中的控制逻辑已经导入dSPACE硬件实验箱的内部控制器，将锂离子电池的外部电路按照下图左半部分所示连接，并将电池的端电压与工作电流通过dSPACE的高速AD采集I/O口采集到内部控制器中。

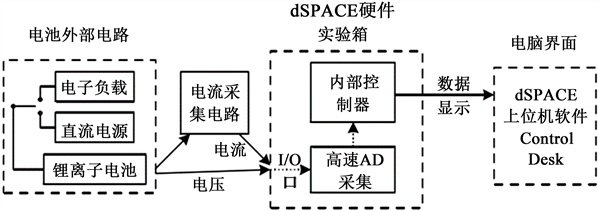
Figure 1. Schematic of operational process for HIL platform

图1. HIL平台运行流程原理图

2.2. 本研究中HIL平台的搭建

基于dSPACE的HIL仿真平台最终硬件搭建如图2所示，其中信号连接用虚线表示，仪器连接用实线表示，电路组成由电池以及并联在正负两端的可编程电源和电子负载构成，可编程电源对电池进行充电，电子负载负责对电池进行放电。电池负极上的继电器开关用来控制电路的通断，控制对电池的充放电；电路的控制和反馈过程由dSPACE完成，它可以对电子负载和可编程电源进行控制，基于整车仿真模型的运行保证电池的充放电按照设定进行，同时还可以对电池的电压、电流、SOC等信息进行实时的采集和监控。

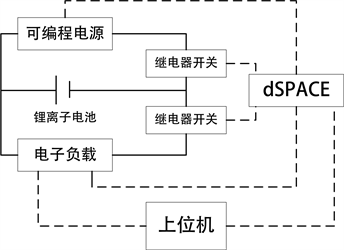
Figure 2. Hardware architecture connection diagram for HIL platform

图2. HIL平台硬件架构连接图

3. 联合仿真模型的建立

3.1. SOE的定义与计算原理

从实际车辆应用的角度来看，目前对SOE的定义主要分为两种类型 [6] 。第一种是“理论剩余能量”，即电池在当前荷电状态下放电至零荷电状态所累积放出的能量，只与当前荷电状态相关。第二种是“剩余可放电能量”，即在某一工况下，电池从当前荷电状态放电至截止电压时所能放出的总能量，与实际行车工况密切相关。后者的计算值可以看作实际放电端电压对实际放电量的积分，与理论剩余能量相比，主要是实际放电端电压曲线、实际放电截至电压以及实际放电电量的不同。

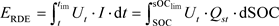(1)

基于上述SOE定义，如下图3，本文将以SOC序列为基准，在考虑工况因素下估计SOC序列对应的实际端电压、实际放电量，最后通过端电压与电量基于SOC序列的积分计算剩余可放电能量SOE，如下式。为此，需要建立联合仿真模型对电池SOE在线估计进行研究。

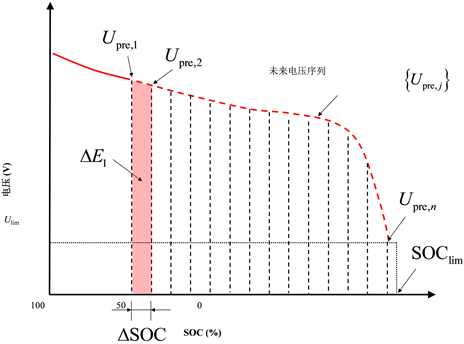
Figure 3. Principle of state of energy (SOE) calculation

图3. SOE计算原理

$\text{Δ}{E}_1\approx \left(U_{\text{pre},1}+U_{\text{pre},2}\right)/2\cdot \text{ΔSOC}\cdot C_{\text{bat}}$ (2)

(3)

3.2. 电池模型

3.2.1. Thevenin等效电路模型

目前，锂离子电池模型主要分为三类：电化学模型、黑盒模型和等效电路模型 [7] 。电化学模型由相互耦合的偏微分方程组成，可以反映充放电过程的状态变化和描述电池内部的电化学反应，但需要相当复杂的数据处理，计算量很大。黑盒模型是基于大量数据，通过神经网络等各种算法建立输入与输出间的非线性关系，准确度很大程度上取决于训练数据的数量、质量和普适性，其“黑盒”特性导致模型不能反应电池的物理特性，缺乏可分析的物理意义。等效电路模型则是基于电池在不同工况下的测试数据，通过拟合等效电路来反映电池的动态特性。

考虑到等效电路模型可以通过串联连接不同时间尺度常数的RC元件来模拟不同时间尺度下的电压响应，因此可以快速模拟电池的外部特性且实现简单易行。因此，在本文中我们选择采用Thevenin等效电路模型。为了获得精确的SOE估计，电池模型需要在短时间尺度和长时间尺度下均具有较高的响应精度。相对于一阶RC模型，二阶RC模型可以更准确地反映电池的动态特性，从而大大提高等效电路模型的精度。同时，与高阶模型相比，二阶RC模型的计算量和复杂度显著降低，而精度仅略低于三阶和四阶模型。因此，本文选用带有二阶RC支路的Thevenin等效电路模型，其结构如下图4所示。针对电池在使用中表现出较强的非线性，SOC估算则采用扩展卡尔曼滤波算法(EKF) [8] 。

Figure 4. Thevenin model

图4. Thevenin模型

该模型主要仿真基于SOC的电动势电压、电池内阻、电池电感、双电层现象、扩散现象，最终得到端电压V_Bat如下式。

$V_{\text{Bat}}=V_{\text{emf}}-V_{\text{Loss}}=n_{\text{Cell}}{V}_{\mathrm{Cell}}\left(\text{SOC}\right)-V_{\text{Loss}}$ (4)

$V_{\text{Loss}}=\frac{1}{C_{\text{DL}}}{{\displaystyle \int }}^{\text{}}\left(I_{\text{Bat}}-\frac{V_{\text{CDL}}}{R_{\text{DL}}}\right)\text{d}t+\frac{1}{C_{\text{Diff}}}{{\displaystyle \int }}^{\text{}}\left(I_{\text{Bat}}-\frac{V_{\text{CDiff}}}{R_{\text{Diff}}}\right)\text{d}t+I_{\text{Bat}}{R}_{\text{Bat}}\left(\text{SOC},I_{\text{Bat}},T_{\text{Bat}},\text{SOH}\right)+\frac{\text{d}{I}_{\text{Bat}}}{\text{d}t}{L}_{\text{Bat}}$ (5)

3.2.2. 电池模型的参数辨识

为了实现对模型参数的精确估计，本文采用卡尔曼滤波算法，该算法对模型参数的精度要求较高。因此，我们需要使用遗传算法对不同SOC处的电池二阶RC模型进行参数辨识，包括欧姆内阻R0、化学极化部分的传荷电阻R1和时间常数τ1，以及浓差极化部分的扩散电阻R2和时间常数τ2。其流程如下图5。这个过程需要使用不同温度和脉冲倍率下的HPPC测试数据，对不同SOC处的模型进行参数辨识。

首先，我们对HPPC测试数据进行预处理，只保留从100% SOC至0% SOC的有效数据段，内容包括电压、电流、时间间隔、SOC值和1 s充放电欧姆内阻数据。然后，对于每个SOC，我们获取对应该SOC的充放电脉冲数据段，包括放电脉冲、搁置和充电脉冲。接着，我们设定欧姆内阻在遗传算法中的允许变化值，并基于允许变化值和1 s充放电欧姆内阻数据计算充放电欧姆内阻的变化范围，以用于后续参数辨识过程。

采用遗传算法进行参数辨识 [9] ：1) 根据经验，设定该SOC范围遗传算法参数变化上下限(包括SOC、容量、充放电欧姆内阻、R1、τ1、R2、τ2)，其中欧姆内阻的变化上下限就是上一步中的“计算值 ± 允许变化值”。(初次辨识将上下限设得宽一些，根据初步辨识结果大致确定参数范围后，重新设定上下限)；2) 设定遗传算法的种群大小和迭代次数。种群数越大，辨识结果可能越准确，但运算时间越长。遗传算法会在两次迭代结果差异小于某一值或迭代次数超过设定值时停止；3) 根据当前SOC和模型参数，计算模型端电压，并结合实测端电压计算端电压均方根误差，用于作为遗传算法中的适应值；4) 将迭代辨识得到的模型参数取出，并存入模型参数向量中。

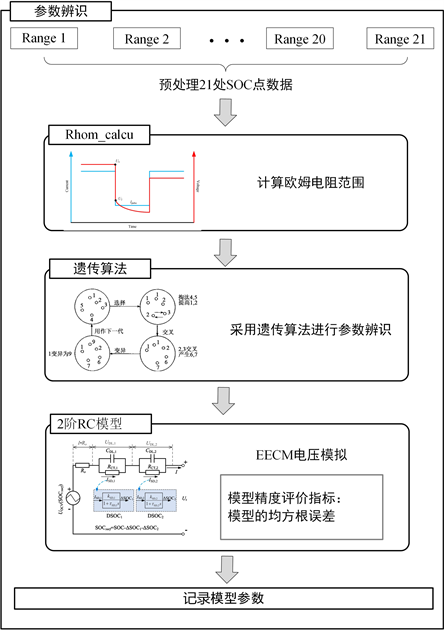
Figure 5. Schematic of parameter identification process

图5. 参数辨识流程原理图

最终得到不同SOC下参数辨识结果如表1。

Table 1. Identification results of battery parameters

表1. 电池参数辨识结果

3.3. 电动汽车整车模型

整车模型主要包含整车动力学模型、驾驶员模型、电动机模型 [10] 。

3.3.1. 整车动力学模型

对电动汽车进行受力分析，车辆行驶过程中主要受到滚动阻力、空气阻力、加速阻力和坡度阻力的作用。

汽车行驶过程中，轮胎滚动时所受到的阻力即滚动阻力，方向与轮胎滚动方向相反。滚动阻力的经验计算公式如式(6)所示。式中，F_z,w表示车轮法向载荷，f_r表示滚动阻力系数，滚动阻力系数可根据经验公式(7)简化计算得到，式中v为车辆的行驶速度。

$F_r=f_r{F}_{z,w}$ (6)

$f_r=f_0+f_1\left(\frac{v}{100}\right)+f_4{\left(\frac{v}{100}\right)}^4$ (7)

车辆行驶过程中，空气流过车身或车内时产生的阻力即空气阻力，可根据式(8)计算。式中，F_d表示空气阻力，C_d表示空气阻力系数，A表示汽车迎风面积，v则表示车辆行驶速度。

$F_d=\frac{1}{21.15}{C}_{d}A{v}^2$ (8)

车辆加减速过程中，整车质量引起的平动分量和旋转部件引起的转动分量的合力即为加速阻力。加速阻力可按式(9)计算，式中F_a,t为平动分量，F_a,r为转动分量。为简化计算，现定义一个旋转质量转换系数，并且令，于是加速阻力可按变形后的式(10)近似计算，可取1.1。

$F_a=F_{a,t}+F_{a,r}$ (9)

$F_a={\delta }_{j}m{v}^{\prime }$ (10)

车辆爬坡行驶过程中，重力沿坡道的分力即坡度阻力，其计算如式(11)所示，式中m为汽车质量，g为重力加速度，为坡道角度。

$F_i=mg\sin \alpha$ (11)

综上所述，可得行驶方程式如式(12)所示。F_t为汽车驱动力，可通过式(13)计算得到，式中T_s为电动机转矩，i_t为传动比，η_t为传动系机械效率。式(12)两边同时乘以车速，经过变形即可得到功率计算表达式如式(14)所示。

$\begin{array}{c}{F}_t=F_r+F_d+F_a+F_i\\ =f_{r}mg\cos \alpha +\frac{C_{d}A{v}^2}{21.15}+{\delta }_{i}m{v}^{\prime }+mg\sin \alpha \end{array}$ (12)

$F_t=\frac{T_s{i}_t{\eta }_t}{r_d}$ (13)

$P_e=\frac{v}{3600{\eta }_t}\left(f_{r}mg+\frac{C_{d}A{v}^2}{21.15}+{\delta }_{i}m{v}^{\prime }+mg\sin \alpha \right)$ (14)

最后确定关键模型参数如表2所示。

Table 2. Simulation model parameters for vehicle

表2. 整车仿真模型参数

3.3.2. 驾驶员模型

整车模型一般分为前向仿真与后向仿真两种，二者在建模方式与应用上均有一定的差异。前向仿真更适合设计后期的应用，可实现控制策略的优化和改进；而后向仿真则更适合应用在设计初期，指导整车部件的选型及控制策略的初步选择。在部件构成上，最大的区别在于前向仿真包含驾驶员模型，而后向仿真不包含驾驶员模型。驾驶员模型可向整车控制器直接发出控制指令，是前向仿真的起始部件。由于本文需要研究电动汽车电池剩余能量的估计和验证，因此选用带有驾驶员模型的前向仿真结构更为合适。

在仿真过程中，驾驶员模型需要根据实际需求车速与仿真车速的偏差，实时调整加速踏板或制动踏板的开度，以此来实现控制器对整车的能量管理和分配，确保控制器按照驾驶员的驾驶意图进行整车控制。仿真过程中，驾驶员对踏板的调节以转矩的形式表现，控制器根据驾驶员的驾驶需求计算出驱动部件应该提供的转矩或功率，从而实现对整车的控制。整个仿真系统的控制信号和能量流向与实际车辆的传输路径相同，即从驱动机构到传动部件，最终传达至车轮以实现车辆的正常行驶。

此处驾驶员模型采用PI控制策略，其控制规律如式(15)所示，式中，v_ref为需求车速，v_fdbk为仿真车速，且参数K_p取值0.3，K_i取值0.05。

$u\left(t\right)=K_p\left(v_{ref}-v_{fdbk}\right)+K_i{\displaystyle {\int }_0^t\left(v_{ref}-v_{fdbk}\right)\text{d}t}$ (15)

3.3.3. 电机模型

本文以永磁同步电动机为建模对象，电动机参数的确定主要包括电动机功率、电动机峰值转矩和电动机转速几个方面。

首先，由最高车速确定额定功率。其应满足车辆在最高车速下稳定行驶的需求，根据式(16)即可计算该需求对应的功率。式中，η_t表示机械效率，取值为0.9；m为整车质量；v_max为最高行驶速度；fr为滚动阻力，取0.015；A表示迎风面积；C_d为空气阻力系数，根据经验取值0.28。计算得额定功率P₁。

$P_1=\frac{v_{\max }}{3600{\eta }_t}\left(mg{f}_r+\frac{C_{d}A{v}^2{}_{\max }}{21.15}\right)$ (16)

其次，由最大爬坡度确定额定功率。车辆在爬坡行驶过程中没有加速运动，因此可根据式(17)来计算对应的功率。式中α_max为最大坡度，取值30%，即17˚；v_i表示爬坡时的车速。计算得到额定功率P₂。

$P_2=\frac{v_i}{3600{\eta }_t}\left[mg\left(f_r\cos {\alpha }_{\max }+\sin {\alpha }_{\max }\right)+\frac{C_{d}A{v}_i{}^2}{21.15}\right]$ (17)

再次，由加速时间确定峰值功率。汽车加速阶段一般比较短暂，但是所需功率很高，所以应通过加速时间的长短来设计峰值功率，其计算公式如式(18)所示。在0~100 km/h加速过程中，vend取100 km/h，加速时间取11 s，其他与前面一致。计算得峰值功率P₃。

$P_3=\frac{v_{end}}{3600{\eta }_t}\left(mg{f}_r+\frac{C_{d}A{v}_{end}{}^2}{21.15}+{\delta }_{j}m\frac{\text{d}u}{\text{d}t}\right)$ (18)

然后，确定电动机峰值转矩。汽车上坡行驶时，所需的转矩最大，忽略加速阻力，即可按式(19)计算电动机的峰值转矩。式中传动比选8.3；v_i为爬坡车速；其它与前面一致。计算得到最大转矩T_max (同时应保留一定的转矩余量)。

$T_{\max }=\frac{\left(mg\left(f_r\cos {\alpha }_{\max }+\sin {\alpha }_{\max }\right)+\frac{C_{d}A{v}_i{}^2}{21.15}\right)r_d}{i_t{\eta }_t}$ (19)

最后，确定电动机峰值转速。电动机的峰值转速可按式(20)进行计算。式中的变量与上面一致。

$n_{\max }=\frac{v_{\max }\cdot i_t}{0.377r_d}$ (20)

最终，获得电动机仿真模型的关键参数如表3所示。

Table 3. Simulation model parameters for electric motor

表3. 电动机仿真模型参数

4. 结果

在建立的HIL平台上，使用某厂家的磷酸铁锂电池进行在环仿真。仿真模拟了以该电池集成的电池组为能源的电动汽车在NEDC和WLTP混合工况下的行驶，并根据仿真结果实时控制电池的充放电，实时采集电池电流电压信息。采用dSPACE实时采集的真实电压电流信息计算得到了SOE的真实值，降噪后作为SOE参考真实值。通过调节优化仿真模型参数和算法，得到了在线估计的SOE结果，如下图6。实验表明，原本的SOE估计值与参考真实值的均方根误差为RMSE = 1.3526，而利用该平台在线调参后的SOE估计值与参考真实值的均方根误差为RMSE = 0.4324，说明优化后的SOE估计更加接近真实值。

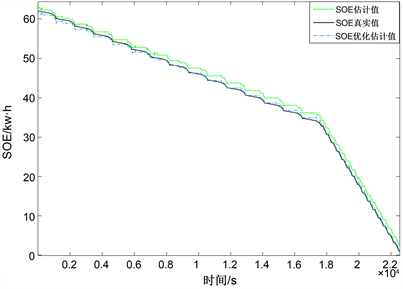
Figure 6. Online estimation results of SOE

图6. SOE在线估计结果

5. 结论

本文中，首先建立了一个基于dSPACE的硬件在环(HIL)仿真平台，将真实电池作为在环硬件接入。接着基于剩余可放电能量SOE的定义确定了SOE的计算方法，并在Simulink环境下搭建了对应的Thevenin等效电路仿真模型和电动汽车整车仿真模型。然后，借助RTW和RTI软件平台的编译和代码的转换，将Simulink仿真模型作为控制逻辑导入dSPACE硬件实验箱的内部控制器。最终，实现了由dSPACE根据仿真模型实时运行的控制逻辑，控制真实锂电池在电动汽车NEDC和WLTP混合工况下作为电池组电芯的充放电，并实时采集和监控真实电池的电流电压数据。最后，本研究基于该HIL仿真平台实时地调试优化动态参数模型和算法，完成了对电池SOE在线估计的研究。

本文通过构建整车模型，从电动汽车实际行驶工况对电池充放电工况的影响出发，考虑驾驶员、电机、车辆动力学、行驶路况等主客观因素的影响，尽量提高对电动汽车电池SOE的估计精度。并在此基础上搭建了HIL平台进行实时测试和基于真实电池充放电响应的调参优化，缩短了进一步提高SOE估计精度和适用性的研究周期。且该HIL平台具有扩展应用性，针对不同工况、不同电池的车载工作状态中的包含SOE在内的各种电池特性的研究具有重要的实际应用价值。