基于GM(1,1)模型和BP神经网络的四川省用电量预测

Production of Electricity Consumption Based on GM(1,1) and BP Neural Networkin Sichuan Province, China

摘要: 随着中国经济的快速增长，人民对能源的需求也在逐步增长。电能作为居民基本的生活能源，其是否能够充足稳定的供应决定了社会经济的运行。当在面对突发事件无法及时满足供电需求时，对于用电量的预测就成为了一种未雨绸缪的重要方法。本文基于GM(1,1)模型和BP神经网络建立了一种新的GM-ABP模型。我们将GM-ABP模型用于预测中国四川省年用电总量。本文提出的模型在GM(1,1)模型的基础上加以修正，利用Adam算法优化的BP神经网络对残差进行拟合。预测结果显示GM-ABP模型的预测精度均优于GM(1,1)模型和Adam-BP神经网络模型，且预测精度有较大提升。最后通过GM-ABP模型给出了四川省2021~2023年用电总量的预测值。

Abstract: With the rapid growth of China’s economy, people’s demand for energy is also gradually increasing. Electric energy is the essential energy of life; its sufficient and stable supply determines the opera-tion of the social economy. When the power supply demand cannot be timely met in the face of emergencies, the forecast of electricity consumption has become a meaningful way to prepare for that. This paper establishes a new GM-ABP model based on GM (1,1) model and BP neural network. We use the GM-ABP model to predict the total annual electricity consumption in Sichuan Province, China. The model proposed in this paper is modified based on the GM (1,1) model, and the residual is fitted by BP neural network optimized by the Adam algorithm. The prediction results show that the prediction accuracy of the GM-ABP model is better than that of the GM (1,1) model and Adam-BP neural network model, and the prediction accuracy is greatly improved. Finally, the GM-ABP model is used to predict the total electricity consumption of Sichuan Province in 2021~2023.

1. 引言

能源是经济发展的基础 [1] 。而对于能源需求的预测则是国家决策和规划的基础。由于电能这种特殊能源具有产出、供给和销售同时进行和动态变化的特点，对于电力需求的预测就显得尤为重要。在2022年，中国四川省因罕见的高温天气导致主要流域缺水，水电供应下降严重。对于此次事件，四川省政府积极应对，调配用电结构，减少不必要用电，保障了人民日常用电需求。由此可见，对于能源需求的预测可以保障人们的生活和社会正常活动，有效地最大限度地降低运行成本，保障经济平稳运行，提高社会经济效益 [2] [3] [4] 。

已经有大量研究对电力能源相关问题进行建模预测 [5] [6] [7] [8] 。建模预测方法可以大致分为四类：统计方法、人工智能方法、灰色系统方法以及混合方法 [9] 。统计方法例如Chu [10] 和Patrícia Ramos [11] 分别利用ARMA和ARIMA方法进行预测研究。Carolina [12] 通过对电力需求的预测分析对比了VAR和iMLP方法的优劣。Takeda [13] 利用Kalman filter (KF)进行电力负荷的预测和分析。但上述方法因为本身固有的弱点，未能给出所预测内容的非线性特征以及数据快速变化时的预测值 [14] 。相比较下，深度学习方向的研究可以弥补上述方法的不足并且也有更好的预测准确性 [15] 。因此，许多研究都基于深度学习的方法进行预测分析。

在众多以深度学习为主的预测研究中，神经网络是最常用和最重要的方法之一。Li [16] 在研究中基于Artificial Neural Network建立了预测模型以对town of Palermo的居民用电量进行短期预测。随着神经网络的发展，BP神经网络算法以其较强的非线性映射能力和自适应能力以及结构简单等优势逐渐成为研究的重点方向。而在BP神经网络中梯度下降算法是研究人员优化的核心，好的优化算法可以加速神经网络找到最小值并且可以有效避免陷入局部最小值等问题。Cinar等人 [17] 建立的预测模型以遗传算法(GA)改进的BP神经网络为基础，预测分析了土耳其未来的能源结构。在上述研究的基础上，Wu等人 [18] 结合了遗传算法(GA)和退火算法(SA)建立了GASA-BP预测模型。相较于传统BP神经网络和遗传算法改进的神经网络而言，GASA-BP在模型迭代次数更少的前提下具有更小的误差，并且运行时间也有大幅优化。Uzlu [19] 和Cinar [20] 采用灰狼优化算法(GWO)分别对温室气体排放量和地区风速进行预测，其误差结果相较于传统BP神经网络均有较大提高。Li et al. [2] 利用粒子群(PSO)算法改进传统BP神经网络，提供了一种应对类似新冠肺炎的紧急事件时的电力预测模型。

除了上述两种的预测方法外，灰色系统理论也是研究不确定性的方法之一，其在不确定信息系统的数学分析方面具有优越性。灰色系统也是一种潜在的构建预测模型的方法 [21] 。即使面对少量数据，灰色系统也可以描述不确定系统的特征 [22] 电力需求的预测也可以看做一个灰色问题，因为电力消耗受多方面因素影响，且不确定各因素的影响强度。另外，对于像中国这样的新兴国家，工业发展晚，数据记录时间短，这样的数据正适合利用灰色系统中的GM(1,1)模型方法进行预测分析。Ding等人 [23] 在GM(1,1)的基础上进行改进，在初始条件中加入了动态加权系数。模型在遵循“新信息优先”时，表现出比传统GM(1,1)模型更好的适应性。研究最后对中国总量和工业用电量进行了预测。Guefano等人 [24] 采用了另一种思路，使用VAR(1)模型来修正GM(1,1)模型，将两种模型进行加权平均以减少单纯使用GM(1,1)模型带来的残差。最终建立了GM(1,1)-VAR(1)模型并预测了喀麦隆居民的用电量。Du等人 [25] 的研究基于多个输出变量的GM(1,n)模型，利用粒子群算法对输入灰色系统的数据进行预处理以满足建模条件，并且利用灰色关联排序确定输入变量个数。最后作者预测了中国江苏省未来几年的用电量，并提出了有关能源管理的政策建议。Xu等人 [26] 提出了一种具有最优时间响应函数的混合GM(1,1)模型，该模型能够对用电量进行预测。Wu等人 [27] 将总人口作为变量之一提出了一种多变量的灰色预测模型。该模型对分数阶累计的GMC(1,1)模型进行了优化，最终预测了中国山东省的用电总量。

相较于上述预测研究中使用的方法，将不同的预测方法相结合在解决某些特定问题时更有效。Hu [28] 提出了基于遗传算法的残差GM(1,1)模型，以中国能源需求为例的实验证明该模型优于其他GM(1,1)模型变体。Hsu等人 [29] 结合了GM(1,1)和人工神经网络提出了一种改进的GM(1,1)模型。作者为原始数据和残差数据分别建立了GM(1,1)预测模型，然后训练人工神经网络以确定残差预测值的符号。Zhu等人 [30] 的研究将不同时间的数据进行动态加权处理，使新数据在GM(1,1)预测模型中占比加大，并且引入粒子群算法(PSO)以确定加权系数和相应时间。作者将提出的SFOGM(1,1)模型与五种预测模型进行残差比较，结果均优于已有模型，最后预测了中国江苏省2020年的用电量。

本文旨在构造一种新的预测模型，以预测中国四川省用电量的准确值。该预测模型在GM(1,1)预测模型的基础上利用改进的BP神经网络对残差部分进行补充，被称为GM-ABP模型。GM(1,1)模型由一个单变量的一阶微分方程构成。其适合对“少数据，贫信息”的原始数据进行分析，所以我们将GM(1,1)模型用于数据预测的第一步。预测数据与真实值之间进行比较，残差部分则由人工神经网络进行训练。在对于传统神经网络的改进方面，我们采用了Adam算法进行改进，既减少了人工神经网络陷入局部最小值的问题，又提高了训练的速度。GM-ABP模型即兼顾了GM(1,1)模型利用小样本预测的适用性，又利用了人工神经网络对于非线性特性的强适应性。最终我们将GM-ABP模型用于预测中国四川省的电力消耗总量，以扩展在解决预测问题上的新思路。

本文的设计工作如下：下一节我们将介绍GM(1,1)模型，传统BP神经网络模型和Adam优化算法。第三节我们将介绍我们提出的新的GM-ABP模型。我们利用GM-ABP模型对中国四川省统计局给出的统计年鉴数据对用电总量进行预测，并将另外两种模型的预测结果与之相比较，这部分在第四节给出。最后一节，我们给出了本文的结论以及一些政策建议，并且在最后讨论了未来的研究方向。

2. 预备知识

2.1. GM(1,1)模型

GM(1,1)模型具有所需样本小，无需考虑数据分布规律，预测精度较高等特点，这些特点也决定了GM(1,1)模型可以被广泛的应用于各个领域。GM(1,1)模型的时间序列数据基于已知的综合信息，用微分方程来近似拟合时间序列的动态过程，然后对时间序列进行推导与达到预测的目的。用来拟合时间序列的是单基一阶微分方程，因此称为GM(1,1)模型 [31] 。具体建模步骤如下：

Step 1：生成累加序列即1-AGO序列。假设有非负序列

$X^{\left(0\right)}=\left(X_{\left(1\right)}^{\left(0\right)},X_{\left(2\right)}^{\left(0\right)},\cdots ,X_{\left(n\right)}^{\left(0\right)}\right)$ (1)

取值的时间间隔相等，并且 $n\ge 4$ 。则有1-AGO序列为

$X^{\left(1\right)}=\left(X_{\left(1\right)}^{\left(1\right)},X_{\left(2\right)}^{\left(1\right)},\cdots ,X_{\left(n\right)}^{\left(1\right)}\right)$ (2)

其中第k个元素为 $X_{\left(k\right)}^{\left(1\right)}={\displaystyle \underset{i=1}{\overset{k}{\sum }}{X}_{\left(i\right)}^{\left(0\right)}}$ ， $k=\left(1,2,\cdots ,n\right)$ 。

Step 2：生成紧邻均值序列。有序列

$Z^{\left(1\right)}=\left(Z_{\left(2\right)}^{\left(1\right)},Z_{\left(3\right)}^{\left(1\right)},\cdots ,Z_{\left(n\right)}^{\left(1\right)}\right)$ (3)

被称为紧邻均值序列，其中 $Z_{\left(k\right)}^{\left(1\right)}=\delta X_{\left(k\right)}^{\left(1\right)}+\delta X_{\left(k-1\right)}^{\left(1\right)}$ ， $k=\left(2,3,\cdots ,n\right)$ ， $\delta =0.5$ 。

Step3：建立灰色微分方程。GM(1,1)模型的均值形式为 $X_{\left(k\right)}^{\left(0\right)}+a{Z}_{\left(k\right)}^{\left(1\right)}=b$ ，则GM(1,1)模型相应的白化微分方程为

$\frac{\text{d}{X}^{\left(1\right)}}{\text{d}t}+a{X}^{\left(1\right)}=b$ (4)

其中a称为发展系数，b称为内生控制灰数。

Step 4：计算系数。设待估向量 $\hat{u}={\left(a,b\right)}^{\text{T}}$ ，利用最小二乘法计算 $\hat{u}={\left(B^{\text{T}}B\right)}^{-1}{B}^{\text{T}}Y$ ，其中 $B=\left[\begin{array}{cc}-Z_{\left(2\right)}^{\left(1\right)}& 1\\ -Z_{\left(3\right)}^{\left(1\right)}& 1\\ ⋮& ⋮\\ -Z_{\left(n\right)}^{\left(1\right)}& 1\end{array}\right]$ ， $Y=\left[\begin{array}{c}{X}_{\left(2\right)}^{\left(0\right)}\\ X_{\left(3\right)}^{\left(0\right)}\\ ⋮\\ X_{\left(n\right)}^{\left(0\right)}\end{array}\right]$ 。

Step 5：得出灰色预测结果。

$\{\begin{array}{l}{\hat{X}}_{\left(k+1\right)}^{\left(1\right)}=\left(X_{\left(1\right)}^{\left(0\right)}-\frac{b}{a}\right){\text{e}}^{-ak}+\frac{b}{a}\hfill \\ {\hat{X}}_{\left(k+1\right)}^{\left(0\right)}={\hat{X}}_{\left(k+1\right)}^{\left(1\right)}-{\hat{X}}_{\left(k\right)}^{\left(1\right)}\hfill \end{array}$ ， $k=1,2,\cdots ,n$ (5)

其中 ${\hat{X}}_{\left(k+1\right)}^{\left(0\right)}$ 即为 $k+1$ 时刻的预测值。

2.2. BP神经网络

BP (back propagation)神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络，是应用最广泛的神经网络模型之一。BP神经网络分为三层即输入层，隐藏层和输出层，具体结构如图1所示。

Figure 1. The structure of BP neural network

图1. BP神经网络结构图

BP算法包括信号的正向传播和误差的反向传播两个过程。正向传播时，输入信号通过隐藏层作用于输出节点，经过非线性变换得到输出信号，完成一次正向传播。反向传播则是将输出误差反向传输给隐藏层，并将误差按权重分摊给各个节点，以各节点获得的误差信号作为调整权重的依据。通过反复学习，使误差沿梯度方向下降，最终按照可接受的最小误差范围结束学习得到结果。在BP神经网络的反向传播中，每个连接权重均需更新。例如更新图1中的权重，更新公式为：

${w^{\prime }}_i=w_i-\eta \frac{\partial \delta }{\partial w_i}$ (6)

其中 $\eta$ 为学习率， $\delta$ 为误差函数。在传统BP神经网络中学习率 $\eta$ 是一个人为固定的值，这就导致函数可能在极值点处来回震荡，导致最终无法收敛。因此我们需要选取一种动态方法对学习率进行修正。学习率关系到神经网络梯度下降的方向及快慢，好的学习率可以优化下降路径减少迭代次数，减少陷入局部最小值的情况。本文就采用了Adam优化器对BP神经网络的梯度下降进行优化。

2.3. Adam优化算法

Adam优化算法是结合了RMSprop优化算法和动量法所提出的优化算法 [32] [33] 。Adam优化算法改进后更新权重的计算公式为：

$w_{\left(t\right)}=w_{\left(t-1\right)}-\frac{\eta }{\sqrt{S_{\left(t\right)}}+\epsilon }\cdot V_{\left(t\right)}$ (7)

其中 $V_{\left(t\right)}={\beta }_1{V}_{\left(t-1\right)}+\left(1-{\beta }_1\right)\Delta w_{\left(t\right)}$ ， $S_{\left(t\right)}={\beta }_2{S}_{\left(t-1\right)}+\left(1-{\beta }_2\right)\Delta w_{\left(t\right)}\cdot \Delta w_{\left(t\right)}$ 。 $V_{\left(t\right)}$ 是指数加权移动平均后t时刻的冲量， $S_{\left(t\right)}$ 是指数加权移动平均后所有梯度的平方和， $\epsilon$ 是一个极小值，防止分母为0。 ${\beta }_1$ 和 ${\beta }_2$ 是两个超参数用于指数加权移动平均。

Adam算法从两方面对权重更新进行了优化。一是加入冲量法的思想，结合历史数据修正不同维度上的分量，减小导致震荡方向的分量，增加方向稳定不变的分量。这样就可以优化下降路径，更快的到达极值点。另一方面，Adam算法中结合了RMSprop算法，利用历史数据对学习率实现自适应。如果对历史数据修改越大，那么学习率减小量也就越大。

3. 构建GM-ABP模型

灰色预测模型可以在不确定系统中对非线性的小数据量的数据进行预测。但当数据发生突变时，灰色预测的误差就会很高。因此我们需要对灰色预测后的数据进行误差补偿。人工神经网络具有强大的学习能力，通过学习可以预测这些突变情况。但如果用人工神经网络完全取代灰色预测也会发生问题。数据在进入人工神经网络需做预处理，否则会造成训练模式过多增加网络结构，降低学习效率，大量消耗资源。另外，单独使用人工神经网络进行预测的数据应是非稀疏的，且数据量越大模式预测越准确，故电力消耗预测问题不适用于单独的人工神经网络。基于以上原因文体提出了利用人工神经网络来建立误差修正模型修正灰色预测结果的GM-ABP模型，GM-ABP模型步骤如图2所示。

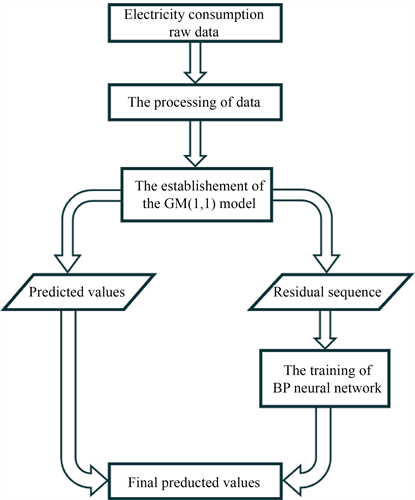
Figure 2. The structure of GM-ABP model

图2. GM-ABP模型流程图

本文所用到的数据均来自中国四川省统计年鉴，我们以2005-2020年电力平衡表中消费总量数据作为原始数据进行分析预测，则有 $E^{\left(0\right)}=\left(E_{\left(1\right)}^{\left(0\right)},E_{\left(2\right)}^{\left(0\right)},\cdots ,E_{\left(n\right)}^{\left(0\right)}\right)$ 。GM-ABP模型具体步骤如下：

Step1：生成1-AGO序列。有序列

$E^{\left(1\right)}=\left(E_{\left(1\right)}^{\left(1\right)},E_{\left(2\right)}^{\left(1\right)},\cdots ,E_{\left(n\right)}^{\left(1\right)}\right)$ (8)

其中 $E_{\left(k\right)}^{\left(1\right)}={\displaystyle \underset{i=1}{\overset{k}{\sum }}{E}_{\left(i\right)}^{\left(0\right)}}$ ， $k=\left(1,2,\cdots ,n\right)$ 。

Step2：生成紧邻均值序列。有序列

$Z^{\left(1\right)}=\left(Z_{\left(2\right)}^{\left(1\right)},Z_{\left(3\right)}^{\left(1\right)},\cdots ,Z_{\left(n\right)}^{\left(1\right)}\right)$ (9)

其中 $Z_{\left(k\right)}^{\left(1\right)}=\delta X_{\left(k\right)}^{\left(1\right)}+\delta X_{\left(k-1\right)}^{\left(1\right)}$ ， $k=\left(2,3,\cdots ,n\right)$ ， $\delta =0.5$ 。

Step3：建立灰色微分方程。GM(1,1)模型的均值形式为 $X_{\left(k\right)}^{\left(0\right)}+a{Z}_{\left(k\right)}^{\left(1\right)}=b$ ，相应的白化微分方程为

$\frac{\text{d}{X}^{\left(1\right)}}{\text{d}t}+a{X}^{\left(1\right)}=b$ (10)

Step4：计算系数。利用最小二乘法计算灰参数a和b。

Step5：得出灰色预测结果。计算方程组

$\{\begin{array}{l}{\hat{E}}_{\left(k+1\right)}^{\left(1\right)}=\left(E_{\left(1\right)}^{\left(0\right)}-\frac{b}{a}\right){\text{e}}^{-ak}+\frac{b}{a}\hfill \\ {\hat{E}}_{\left(k+1\right)}^{\left(0\right)}={\hat{E}}_{\left(k+1\right)}^{\left(1\right)}-{\hat{E}}_{\left(k\right)}^{\left(1\right)}\hfill \end{array}$ ， $k=1,2,\cdots ,n$ (11)

得到 $k+1$ 时 $E_{\left(k+1\right)}^{\left(0\right)}$ 的预测值。

Step6：得到残差序列。原始数据与预测数据之间的差为残差序列。残差序列为：

$e_{\left(k\right)}^{\left(0\right)}=E_{\left(k\right)}^{\left(0\right)}-{\hat{E}}_{\left(k\right)}^{\left(0\right)}$ (12)

Step7：训练人工神经网络。将残差序列作为输入，k时的误差项 ${\hat{e}}_{\left(k\right)}^{\left(0\right)}$ 作为输出训练Adam算法优化的BP神经网络。然后将前k期的残差作为输入放入BP神经网络中，此时的输出 ${\hat{e}}_{\left(k+1\right)}^{\left(0\right)}$ 即是 $k+1$ 时的预测残差。

Step8：得到最终预测值。最终预测值为：

$E_{\left(k+1\right)}={\hat{E}}_{\left(k+1\right)}^{\left(0\right)}+{\hat{e}}_{\left(k+1\right)}^{\left(0\right)}$ (13)

4. 四川省用电量预测

4.1. GM-ABP模型预测

我们统计了2005年至2021年中国四川省统计局发布的统计年鉴，将2010年至2020年用电数据进行分析。最终通过GM-ABP模型对中国四川省2021年至2023年的用电量进行预测。2010~2020年中国四川省用电量如表1所示：

Table 1. Electricity consumption in Sichuan Province (100 million kWh)

表1. 四川省用电量(100 million kWh)

将原始数据带入GM-ABP模型，通过公式(8)和公式(9)分别得到1-AGO序列和紧邻均值序列，最终的紧邻均值序列为：{1548.48，2666.95，3873.59，5172.415，6627.865，8383.63，10369.68，12366.78，14386.68，16420.98，18478.18，20631.28，22963.63，25511.28，28269.28}。再利用最小二乘法计算得到白化方程的灰参数a = −0.044353，b = 1701.793968。利用公式(10)计算得出拟合结果如表2所示。并且通过初步预测可以得出2021~2023年用电量的预测值分别为3002.08，3188.32，3386.10 (100 million kWh)，此时的预测值并非最终预测结果，还需要BP神经网络部分进行误差修正。

Table 2. Fitted electricity consumption of the GM(1,1) model (100 million kWh)

表2. GM(1,1)模型的拟合用电量(100 million kWh)

通过公式(11)计算残差序列，并作为BP神经网络的输入。GM-ABP模型的人工神经网络部分采用双隐藏层的BP神经网络，以6年的数据作为输入，预测下一年的总用电量值。采用双隐藏层的原因是双隐藏层可以表示任意精度的决策边界，可以更好的映射非线性数据。在对2022年和2023年总电量的预测过程中，我们分别将模型给出的2021年和2022年的预测值作为输入值，再通过GM-ABP模型给出最终预测值。最终预测得到2021~2023年用电总量分别为：3245.55，3328.90，3475.96 (100 million kWh)。

4.2. 模型预测结果分析

因为GM-ABP源于GM(1,1)模型和Adam-BP神经网络模型的结合，因此我们将这两种模型的预测结果与GM-ABP模型的结果相比较，以验证模型在电力预测方面的准确性。GM-ABP模型的拟合图像如图3所示。三种模型对于中国四川省2012~2020年用电总量的预测图像如图4所示。

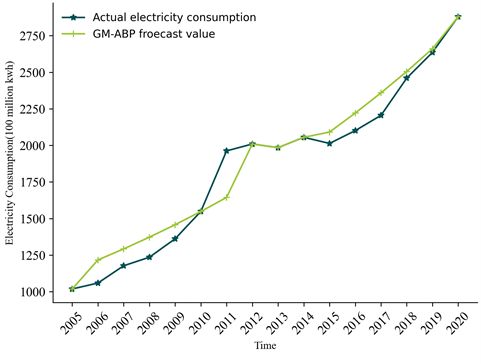
Figure 3. The fitting diagram of the GM-ABP model

图3. GM-ABP模型拟合图

Figure 4. The fitting comparison of GM(1,1), BPNN, and GM-ABP model

图4. GM(1,1)、BPNN、GM-ABP拟合比较

我们采用平均绝对误差(MAE)，平均绝对百分比误差(MAPE)，均方误差(MSE)，均方根误差(RMSE)，决定系数(R²)五类误差数据对GM-ABP模型的预测精度进行检验。设 $f\left(x_i\right)$ 为第i个数据的真值， $\hat{f}\left(x_i\right)$ 为第i个数据的预测值，n为数据总量。五种误差数据的计算公式如下：

$\text{MAE}\left(f\left(x_i\right),\hat{f}\left(x_i\right)\right)=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|f\left(x_i\right)-\hat{f}\left(x_i\right)\right|}$ (14)

$\text{MAPE}\left(f\left(x_i\right),\hat{f}\left(x_i\right)\right)=\left(\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|\frac{f\left(x_i\right)-\hat{f}\left(x_i\right)}{f\left(x_i\right)}\right|}\right)\ast 100\%$ (15)

$\text{MSE}\left(f\left(x_i\right),\hat{f}\left(x_i\right)\right)=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(f\left(x_i\right)-\hat{f}\left(x_i\right)\right)}^2}$ (16)

$\text{RMSE}\left(f\left(x_i\right),\hat{f}\left(x_i\right)\right)=\sqrt{\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(f\left(x_i\right)-\hat{f}\left(x_i\right)\right)}^2}}$ (17)

$R_{\left(f\left(x_i\right),\hat{f}\left(x_i\right)\right)}^2=1-\frac{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(f\left(x_i\right)-\hat{f}\left(x_i\right)\right)}^2}}{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(f\left(x_i\right)-\bar{f}\left(x\right)\right)}^2}}$ (18)

三种模型的误差表现如表3所示：

Table 3. Error representation of the three models

表3. 三种模型的误差表现

根据上表所示，GM-ABP模型在MSE，RMSE，MAE，MAPE数据方面均优于另外两种模型。另外GM-ABP模型R²数值达到0.944说明模型拟合程度较好，具有对用电量数据准确预测的能力。在图中我们还得出，人工神经网络对GM(1,1)模型的补充效果很明显，前三种误差值平均减少了35.71%，并且提高了GM(1,1)模型预测的拟合程度。GM-ABP模型的MSE值相较于Adam-BPNN模型提高了85.46%。另外，我们发现GM(1,1)相较于Adam-BPNN模型更适用于电力预测模型，说明我们利用GM(1,1)模型进行趋势预测并加以BPNN的修正是正确的。综上所述，GM-ABP模型在用电量预测问题上优于GM(1,1)模型和Adam-BPNN模型，且在预测结果上有很好的表现。

5. 研究结论与政策建议

5.1. 研究结论

本文基于GM(1,1)模型和BP神经网络建立了新的GM-ABP模型。我们将GM-ABP模型用于中国四川省年用电总量的预测，并与传统GM(1,1)模型和Adam-BP神经网络模型进行了比较，证明了该模型的优越性。本文提出的模型在GM(1,1)模型的基础上加以修正，利用Adam算法优化的BP神经网络对残差进行拟合。结果显示GM-ABP模型的预测精度均优于GM(1,1)模型和Adam-BP神经网络模型，且预测精度有较大提升。最后通过GM-ABP模型给出了四川省2021~2023年用电总量的预测值。

5.2. 政策建议

随着中国经济的不断高速增长，用电量激增导致的问题日益突出。四川省目前所有的常规发电方式中，水利发电最为突出。2021年，四川省全年发电量4530.33 (100 million kWh)，其中水电3531 (100 million kWh)，占比高达77.95%。2022年，四川省就因罕见的高温天气导致主要流域缺水，水电供应下降严重。对于用电量的提前预测就可以预防用电高峰时用电紧张的问题，做到未雨绸缪。另外降水量和蓄水量的多少直接影响着水利发电能力，因此对于区域的水文监测必不可少。对于电力存储的研究也是保障用电稳定的一方面。

5.3. 未来研究方向

本文提出的GM-ABP模型可以很好地解决用电量预测的问题，但也存在一定的局限性。例如，影响用电量的因素有很多，类似极端高温天气这类的突变因素很大程度会影响年用电量。因此，在未来可以将此类因素造成的影响进行量化，加入模型的预测中。

NOTES

^*通讯作者。