1. 引言
图的Steiner问题是经典的组合优化问题。1989年,Chartrand等 [1] 引入了Steiner距离的概念并进行了初步的研究。Mao等 [2] 在2018年研究了笛卡尔积和字典序积的Steiner距离,并在Steiner距离的基础上给出了Steiner直径的上下界。2019年,Wang等 [3] 接着研究了阈值图、联结图、corona积、cluster积的Steiner距离和Steiner直径,引入了有关Steiner树的概念,运用Steiner树的结构特征证明了相关定理。其余有关Steiner距离的研究可参考Mao等 [4] [5] [6] ,Oellermann等 [7] 的工作。
乘积图的提出是基于这样一种思想,即利用乘积作为一种工具,将两个具有既定性质的已知图组合起来,得到一个新的图,该图继承了这两个图的性质。2009年,Eliasi等 [8] 引入了F-sum图的概念,研究了F-sum图的一般距离。本文对corona积,cluster积,F-sum图的Steiner半径、Steiner距离、Steiner直径进行研究。有关这三个乘积图 [9] - [18] 的一些参数及拓扑指数也得到了充分研究。
本文中所有图都是连通的简单无向图,且顶点个数至少为两个。假设G是一个连通图,顶点
,则
表示顶点
之间最短路的长度。令S是G的一个非空集合且
。点集S的Steiner距离
表示包含S的最小连通子图的边数,特别地,这个最小的连通子图一定是一颗树,令它为S-Steiner树。令k是一个整数且
,则图G中顶点v的Steiner k-离心率
被定义为
。此外,Steiner k-直径和Steiner k-半径的定义为
和
。连通图G的中心
是由
的顶点v诱导的子图,作为图中心的推广,连通图G的Steiner k-中心
是由最小Steiner k-离心率顶点导出的子图,其中
。
Corona积,Cluster积 [19] 和F-sum图 [8] 的定义如下:
定义1 Corona积
通过复制一个G,复制
个H,然后将复制的第i个H的每一个顶点与G的第 个顶点连接起来,其中
。设G和H是两个连通图,顶点集分别为
和
,则
的顶点集为
。
个顶点连接起来,其中
。设G和H是两个连通图,顶点集分别为
和
,则
的顶点集为
。
定义2 Cluster积
通过复制一个G,复制
个根图H,然后将复制的第i个根图H的根与G的第i个顶点相连,其中
。设G和H是两个连通图,顶点集分别为
和
,则
的顶点集为
。
定义3 F-sum图
的顶点集为
。
中的两个顶点分别为
和
,这两个顶点相邻当且仅当
且
或者
且
。
和T的定义如下:
:在图 中的每条边上添加一个新的顶点,使得每条边都由长度为2的路替换所得的图。
中的每条边上添加一个新的顶点,使得每条边都由长度为2的路替换所得的图。
:在图G中的每条边上添加一个新的顶点,在图G的基础上,将每个新顶点连接到相应边的端点上所得的图。
:在图G中的每条边上添加一个新的顶点,将新顶点与相邻的顶点相连所得的图。
:将
和
结合所得的图。
其中,F代表图变换
和T中的一个。
下面给出两个重要的引理。
引理1 [3] G和H是两个连通图,其中
,
。令
是三个整数且
。S是
的顶点各不相同的集合,使得
。则有
,
其中
,
是
的最大子集使得对于任意的
都有
。
引理2 [3] 令点集S是Cluster积
的一个顶点各不相同的顶点集,如果存在
中的顶点在不同的
中,则
,
其中,当
,
时,有
。否则,令
,
,
是
的最大的子集使得对每一个
都有
。
2. 主要结果
2.1. Corona积和Cluster积的Steiner k-半径
定理1 令
是三个整数且
,连通图
分别有n和m个顶点。
如果
,那么
。
如果
,那么
。
如果
,那么
。
证明 以上三种情况的证明方法相同,这里仅考虑第二种情况。如果
,根据
的定义,可以发现存在一个顶点子集
,并且
使得
。令
,其中
。当
时,由引理1可得
(1)
另一方面,选择
使得
。则任意的S-Steiner树T一定包含
中的所有顶点(树T的大小至少是
),且令T的子树为
。对于
中的每一个顶点,至少需要一条边去连接它和
中的顶点,因此可以得到
(2)
由不等式(1)和(2),可以得出结论
。
定理2 令
和n三个正整数且
,令连通图
分别有
个顶点。
如果
,那么
。
如果
并且
,那么
。
如果
并且
,那么
。
如果
,那么
。
如果
,那么
。
证明 首先讨论
以上五种情况的上界。根据
的定义,可知存在一个顶点子集
且
,使得
。令
,
。其中
且
。由引理2可得
。
首先证明结论a)。如果
,则有
,
,并且
。因此
。
其次证明结论b)。如果
且
,则有
,并且
。因此
。
接着证明结论c)。如果
且
,可知
,
,并且
。因此
。
然后证明结论d)。如果
,可知
,
,并且
。因此
。
最后证明结论e)。显然可以得到
。
另一方面,由引理2可知
。且令
,
。对结论a)的下界进行证明,如果
,对于任意的S-Steiner树T一定包含
中的所有顶点(树T的大小至少是
),假设树T有子树
。对于每一个
中的顶点,需要至少一条边来连接它和
中的顶点,最终得到
。
结论b)和结论e)的证明与结论a)的证明类似。对于c)和d)中的情况,证明过程与其上界的证明完全一样。
推论1 假设
,
且
。对每一个
有
和
。如果
,则
;如果
,则
。
推论2 假设
,
且
。对每一个
有
和
。如果
,则
。
2.2. F-Sum图的Steiner距离
令G和H是两个连通图,并且
(
是图G的边数),k是一个整数。令
是F-sum图
的一个顶点各不相同的顶点集,其中F代表
和T中的其中一个。首先介绍几个参数:
• 令
是H的一个复制,其中
。
• 令
是集合
的(k-3)-重子集,其中
。令
是
中每个集合中不同顶点的个数,其中
。
• 令
是集合
的(k-3)-重子集,其中
。令
是
中每个集合中不同顶点的个数,其中
。
定理3 根据上面的定义,可以得到重集
和
。则
证明 根据对称性,这里只考虑
的情况。当
,假设
是
的r个复制,使得
,
。因此
。接下来,考虑三种情况:
情况1.
(S中的所以顶点都是实心的)且
。
由任意性,假设
,那么可以得到顶点
。
中存在一个大小为
的
-Steiner树,则在
中存在一个大小为
且包含顶点
的Steiner树,令这个Steiner树为
。
每一个
都有一个相对应的Steiner树
。所以
是一个大小为
且包含
中的顶点
的Steiner树。同样的,H也有一个大小为
的
-Steiner树。因此
包含
中的顶点
并且大小为
的Steiner树(见图1)。
如果
,则
的一个S-Steiner树是由边
组成。由b的定义可得
或
,则有
。
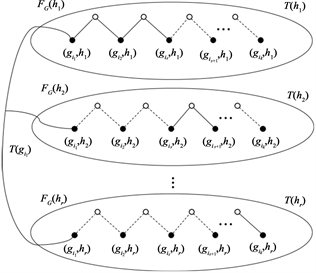
Figure 1. All vertices in S are solid
图1. S中的所以顶点都是实心的
如果
,其中
。若
,
的一个S-Steiner树是由边
组成,由b的定义可知
。若
或
,则
的一个S-Steiner 树是由边
组成,根据b的定义,可以得到
或者
,则
。
情况2.
(S中的所有顶点都是空心的)且
。
由任意性,假设
。则
,其中
。
对于每一个
都有与之相对应的Steiner树
。因此
是大小为
且包含
中k个顶点的Steiner树。同样的,图H有一个大小为
的
-Steiner树,因此
是一个大小为
且包含
中的r个顶点的Steiner树(见图2)。
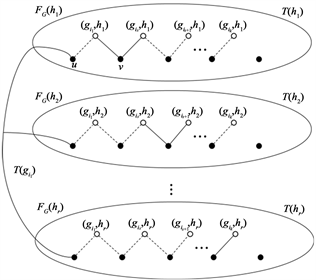
Figure 2. All vertices in S are hollow
图2. S中的所有顶点都是空心的
根据
的定义,对于任意的两个顶点
和
,且
。因此不能直接连接
中的
和
中的
。由任意性,假设
,
,即需要一条边去连接顶点u和
,那么
和
需要r条边去连接。
如果
,则
的一个S-Steiner树是由边
组成,根据b的定义可知
或
,则
。
如果
,其中
。若
,则
的一个S-Steiner树是由边
组成,由b的定义,可得
。若
或者
,则
的一个S-Steiner树是由边
组成,由b的定义可得
或
。即
。
情况3. 存在两个顶点
,
,其中顶点
,
。
每一个
都有与之相对应的Steiner树
。因此
是一个大小为
且包含
的顶点
的Steiner树。同样地,H有一个大小为
的
-Steiner树,因此
是一个大小为
且包含
中顶点
的Steiner树(见图3)。
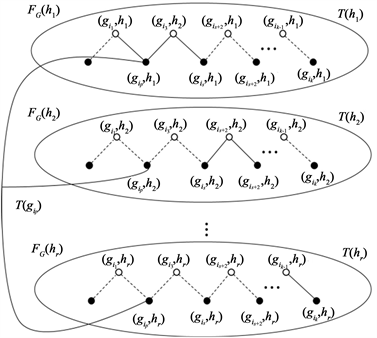
Figure 3. S contains two types of vertices
图3. S中包含两种类型的顶点
情况3的连接方式与情况1类似,即可证
。
现在来考虑下界。令
,其中
,
。根据图
的结构特征,显然
。
推论3 G和H是两个连通图,且
是一个整数。令
是
的一个顶点各不相同的集合。令
,
。如果
且
,则
,其中F代表
和T中的其中一个。
是H的一个复制,且
。
推论4 令G和H是两个阶数分别为
的连通图,令
是三个整数,并且
(
是图G的边数),
。假设
是H的一个复制, 可以知道
,F-sum图的Steiner直径如下
如果
,则
如果
,则
如果
,则
。
3. 结论
本文基于先前建立的关于图乘积的Steiner距离的结果,推广并证明了两个图的corona积和cluster积的Steiner半径,并用来自两个原始图的参数来表示它们。然后,在F-sum图中给出了Steiner距离的界,这反过来又有助于界定F-sum图的Steiner直径。以上得到的主要定理也可以应用于特殊图,并提供了简单的推论。
基金项目
国家自然科学基金项目(12201273);浙江省自然科学基金项目(LY21A010002)。
NOTES
*通讯作者。