基于张量分解的DS-CDMA盲数据检测研究

Research on Blind Data Detection for DS-CDMA Based on Tensor Decomposition

摘要: 为了节约建造天线的成本，本文借助张量分解技术，在DS-CDMA系统中建立PARAFAC模型，固定用户数量(6)、扩频码数(4)和符号快照的块长度数(50)，改变信噪比和天线的数量，通过蒙特卡洛方法模拟生成多维阵列信号，执行COMFAC算法进行盲数据检测来求出误码率，进而在相同的信噪比条件下将误码率与天线数量进行数据拟合，最后结合拟合函数曲线和拟合方程得出最优天线数。研究结果表明拟合优度都达到90%以上，高信噪比的最优天线数少，稳定为5根；低信噪比的最优天线数多，并且不稳定。

Abstract: In order to save the cost of antenna construction, the PARAFAC model is established in DS-CDMA system by means of tensor decomposition technology. Then the number of users (6), spread spec-trum code (4) and block length of symbolic snapshot (50) are fixed. Also the signal-to-noise ratio and the number of antennas are changed. Multi-dimensional array signal is simulated by Monte Carlo method. COMFAC algorithm is used to detect blind data to calculate bit error rate. Then, under the same SNR condition, the bit error rate and the number of antennas were fitted. Finally, the op-timal number of antennas was obtained by combining the fitting function curve and fitting equa-tion. The results show that the goodness of fit is more than 90%, and the number of optimal anten-nas with high signal-to-noise ratio is less, and the stable number is 5. The optimal antennas with low signal-to-noise ratio are numerous and unstable.

1. 引言

张量是描述多维向量和对偶空间的笛卡尔上多重映射关系的几何体 [1] ，是进行多维阵列信号处理的有力工具 [2] 。随着科技的飞速发展，扩展频谱通信技术是现代通信技术的热点之一。因此，国内外学者对张量分解技术在直接序列码分多址(Direct Sequence-Code Division Multiple Access, DS-CDMA)盲数据检测中的应用进行大量的研究。

Sidiropoulos N D等人建立了平行因子分析(Parallel Factor Analysis, PARAFAC)模型与DS-CDMA系统盲多用户分离均衡检测之间的联系，基于低秩三向阵列分解和三线性交替最小二乘回归的唯一性，提出了一种确定性盲PARAFAC接收机，研究结果表明：该接收机具有性能接近非盲最小均方误差的优点 [3] 。Sørensen M等人介绍几种正交约束条件下的PARAFAC的数值算法，这就为不相关信号的接收提供了基础，经过研究结果发现PARAFAC接收机的性能最好 [4] 。Fernandes C A R等人提出了用于上行多用户协同分集系统的新型盲接收机，同时还引入CANDECOMP/PARAFAC (CP)模型，最后通过计算机模拟结果发现各项性能显著提高 [5] 。上述研究表明PARAFAC模型在盲多用户分离检测中的优越性。

在PARAFAC模型的基础上，刘旭和许宗泽研究DS-CDMA系统的盲检测算法，并且提出一种基于正交约束的PARAFAC的DS-CDMA盲接收机，通过研究结果发现具有正交约束的三线性最小二乘算法在处理DS-CDMA比传统的三线性最小二乘算法有更低的克拉美罗界。此外，正交约束–平行因子分析接收机改善了误码率的性能，收敛速度也大大提高 [6] 。Bro R等人提出了复平行因子分析(Complex Parallel Factor Analysis, COMFAC)算法，该算法用于三线性并行因子分析模型拟合到DS-CDMA信号中，同时基于对若干辅助子程序的组合和改进，研究结果表明：算法达到缩短计算时间的目的 [7] 。De Lathauwer L和Castaing J提出了一种基于张量的DS-CDMA信号在天线阵列上的盲分离机制，研究结果表明：相对较高的用户数量，新技术比ALS (Alternate Least Squares)算法计算盲接收机更加准确，并且计算要求更低 [8] 。曾卉露提出基于复平行因子多故障盲分离方法，克服了传统算法在分解的时候运算时间比较长的困难，通过研究发现了方法的有效性 [9] 。于桂晨提出一种基于耦合随机投影和耦合张量分解的大规模张量分解算法，通过对比研究结果表明大规模张量分解算法比传统的算法具有更高的精度；而相对传统张量分解算法虽然有性能损失，但是获得了更少的空间占用和更快的运行效率 [10] 。上述研究表明基于张量分解的算法相对于传统的算法而言，具有提高收敛速度、缩短计算时间等显著的优点。

基于张量分解的技术，蒙特卡洛思想在模拟仿真阶段起着关键性的作用。张珽研究了蒙特卡洛方法在通信系统中采用不同的调制方式下受高斯白噪声信道影响的误码率，并且通过研究证明蒙特卡洛方法的正确性 [11] 。曾璐和谢晓尧通过MATLAB研究不同噪声在直接序列扩频通信系统中误码率与信噪比之间的关系，结果表明：数字信号在复高斯白噪声信道产生的误码率比在高斯白噪声信道中产生的误码率略大 [12] 。

综上所述，国内外相关专家、学者对张量分解技术在DS-CDMA盲数据检测中的应用进行了非常深入的研究。本文就是在DS-CDMA系统中建立PARAFAC模型进行分解，通过蒙特卡洛方法模拟生成多维阵列信号，借助COMFAC算法对模型求解得到误码率的大小，最后在相同的信噪比条件下，将误码率与天线数进行数据拟合来研究在各个信噪比条件下最优天线的个数，在仿真实验中发现规律来达到节约资源的目的。

2. 张量的理论基础

本小节主要介绍有关张量的数学理论知识，包含张量的数学表示和基本的运算。张量是一个定义在一些向量空间和一些对偶空间的笛卡尔积上的多重线性映射 [13] ，是多维数组的简称。本文研究的重点是张量在通信领域中的应用问题，因此，本小节主要以三阶张量为主展开介绍。

2.1. 张量的表示

1) 三阶张量

三阶张量通常用花体符号表示，记作 $\chi \in {ℂ}^{L\times M\times N}$ ，它的元素表示为 $X_{lmn}，l\in L,m\in M,n\in N$ 。 $L、M、N$ 表示三个不同的维度，结合不同的实际问题就是代表三个不同的物理意义。

2) 张量纤维

三阶张量的三路阵列称为张量纤维，即改变一个下标，固定其他下标不变得到每一路阵列。三阶张量可以用不同的模式来表达。模式-1表示三阶张量的行纤维，记作 $X_{l:n}$ ；模式-2表示三阶张量的列纤维，记作 $X_{:mn}$ ；模式-3表示三阶张量的管纤维，记作 $X_{lm:}$ 。对于高阶张量，模式-n表示N阶张量有N种不同的纤维。

3) 张量切片

张量切片是指将三阶张量按照指定单个索引将产生一个特定方向的矩阵。模式-1表示水平切片，记作 $X_{l::}$ ；模式-2表示侧面切片，记作 $X_{:m:}$ ；模式-3表示正向切片，记作 $X_{::n}$ 。

4) 张量的矩阵化

张量的矩阵展开是对高阶张量进行降维的过程。对张量 $\chi \in {ℂ}^{L\times M\times N}$ 进行n模展开，记作 $ma{t}_n\left(\chi \right)$ 或者 $X_{\left(n\right)}$ 。按照Kiers水平展开方式 [14] 进行矩阵化，可以得到模式-1、模式-2、模式-3的水平展开分别为如下式所示：

$X_{\left(1\right)}=X^{L\times MN}=\left[X_{::1},\cdots ,X_{::N}\right]$ (1)

$X_{\left(2\right)}=X^{M\times LN}=\left[X_{1::},\cdots ,X_{L::}\right]$ (2)

$X_{\left(3\right)}=X^{N\times LM}=\left[X_{:1:},\cdots ,X_{:M:}\right]$ (3)

如图1所示是具体描述了三阶张量 $\chi \in {ℂ}^{L\times M\times N}$ 的Kiers水平展开模式。

2.2. 张量的运算

1) 张量的外积

对于N阶张量 $A\in {ℂ}^{I_1\times I_2\times \cdots \times I_N}$ 和M阶张量 $B\in {ℂ}^{J_1\times J_2\times \cdots \times J_M}$ ，上述二者外积定义为 $C=A\circ B$ ，其中 $C\in {ℂ}^{I_1\times I_2\times \cdots \times I_N\times J_1\times J_2\times \cdots \times J_M}$ ，具体如下所示：

$c_{i_1,i_2,\cdots ,i_N,j_1,j_2,\cdots ,j_M}=a_{i_1,i_2,\cdots ,i_N}\cdot b_{j_1,j_2,\cdots ,j_M}$ (4)

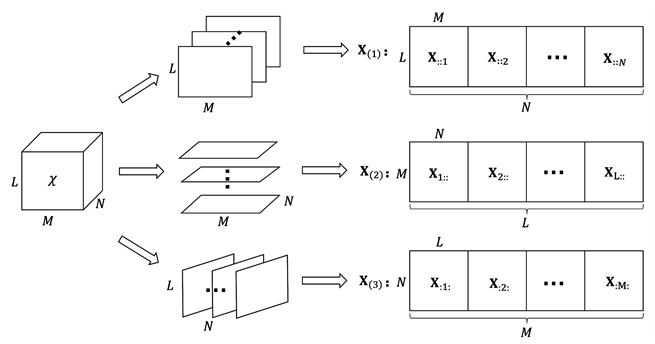
Figure 1. Kiers horizontal expansion of third order tensors

图1. 三阶张量的Kiers水平展开图

2) 张量的内积

对于N阶张量 ${\chi }_1\in {ℂ}^{I_1\times I_2\times \cdots \times I_N}$ 和张量 ${\chi }_2\in {ℂ}^{I_1\times I_2\times \cdots \times I_N}$ ，它们的内积定义如下所示：

$\langle {\chi }_1,{\chi }_2\rangle \stackrel{def}{=}\langle vec\left({\chi }_1\right),vec\left({\chi }_2\right)\rangle =\left(vec{\left({\chi }_1\right)}^{H}vec\left({\chi }_2\right)\right)={\displaystyle \underset{i_1=1}{\overset{I_1}{\sum }}{\displaystyle \underset{i_2=1}{\overset{I_2}{\sum }}\cdots {\displaystyle \underset{i_n=1}{\overset{I_N}{\sum }}{a}^{*}{}_{i_1,i_2,\cdots ,i_n}}}}{b}_{i_1,i_2,\cdots ,i_n}$ (5)

3) 张量的Frobenius范数

定义张量 $\chi$ 的Frobenius范数为：

${\Vert \chi \Vert }_F=\sqrt{\langle \chi ,\chi \rangle }$ (6)

4) Kronecker积

对于任意二维矩阵 $A\in {ℂ}^{I\times J}$ 和矩阵 $B\in {ℂ}^{M\times N}$ 的Kronecker积是一个 $IM\times JN$ 的矩阵，记作 $A\otimes B$ ，具体运算过程如下所示：

$A\otimes B=\left[\begin{array}{cccc}{a}_{11}B& a_{12}B& \cdots & a_{1n}B\\ a_{21}B& a_{12}B& \cdots & a_{2n}B\\ ⋮& ⋮& \ddots & ⋮\\ a_{m1}B& a_{m2}B& \cdots & a_{mn}B\end{array}\right]\in {ℂ}^{IM\times JN}$ (7)

5) Khatri-Rao积

任意两相同列数的矩阵 $A\in {ℂ}^{K\times J}$ 和 $B\in {ℂ}^{I\times J}$ 的Khatri-Rao积记作 $A\odot B$ ，具体如下所示：

$A\odot B=\left[a_1\otimes b_1,a_2\otimes b_2,\cdots ,a_j\otimes b_j\right]\in {ℂ}^{KI\times J}$ (8)

其中Khatri-Rao积还有如下的运算性质 [15] ：

$A\odot B=\left[\begin{array}{l}B{D}_1\left(A\right)\\ B{D}_2\left(A\right)\\ ⋮\\ B{D}_j\left(A\right)\end{array}\right]$ (9)

$\left(A\otimes B\right)\left(C\odot D\right)=AC\odot BD$ (10)

其中 $D_j\left(A\right)$ 表示 $J\times J$ 的对角矩阵，其中的元素表示矩阵 $A$ 中的第j行中的元素。

6) Kruskal秩

任意一个矩阵 $A\in {ℂ}^{I\times J}$ 的Kruskal秩，记为k-秩或者 $k_A$ ，它表示矩阵的任意r个列向量都是线性无关的最大整数 [16] 。矩阵的k-秩小于等于矩阵的秩。如果由列向量构成的矩阵 $A\in {ℂ}^{K\times J}$ ，并且这些列向量是从绝对连续分布中独立提取出的元素，矩阵不仅满秩而且满足k-秩，即 $rank\left(A\right)=k_A=\min \left(I,J\right)$ [16] 。

7) 秩一张量

如果一个三阶张量 $\chi \in {ℂ}^{L\times M\times N}$ 当且仅当它能表示成三个向量的外积的形式，即

$\chi =a_1\circ a_2\circ a_3$ (11)

称此张量为秩-1张量。对于N阶张量，以此类推。

3. 模型的建立

3.1. PARAFAC模型(Parallel Factor Analysis)

PARAFAC (Parallel Factor Analysis)模型中文解释为平行因子分解法，又被称作CANDECOMP、PARAFAC或者CANDECOMP/PARAFAC (CP)。它实际上是对高维张量进行拆分的方法，其核心思想是用有限个秩1张量的和来近似某一个张量，使其误差达到最小的目的。PARAFAC模型在统计学、信号处理中得到广泛应用。

任意一个 $I\times J\times K$ 三阶张量 $\chi$ ，其中的每一个元素记为 $x_{ijk}$ ， $i=1,2,\cdots ,I$ ， $j=1,2,\cdots ,J$ ， $k=1,2,\cdots ,K$ 。 ${\chi }_i\left(J\times K\right)$ 、 ${\chi }_j\left(I\times K\right)$ 和 ${\chi }_k\left(I\times J\right)$ 表示三阶张量在三个不同的方向上的切片，其中元素的对应关系如下所示：

${\chi }_i\left(j,k\right)={\chi }_j\left(i,k\right)={\chi }_k\left(i,j\right)=x_{ijk}$ (12)

得到PARAFAC模型如下式所示：

$x_{ijk}={\displaystyle \underset{f=1}{\overset{F}{\sum }}{a}_{if}{b}_{jf}{c}_{kf}+e_{ijk}}$ (13)

其中 $a_{if}$ 、 $b_{jf}$ 和 $c_{kf}$ 都是要估计的参数，而 $e_{ijk}$ 残差项， $F$ 表示成分的求和数量。 ${\chi }_k$ 表示三阶张量按照第k个模式展开得到 $I\times J$ 的矩阵，那么可以得到PARAFAC模型：

${\chi }_k=A{D}_k{B}^{\text{T}}+E_k$ (14)

其中矩阵 $A$ 表示含有元素 $a_{if}$ 的 $I\times F$ 阶矩阵，同理矩阵 $B$ 是 $J\times F$ 阶矩阵，但是 $D_k$ 表示对角矩阵，包含 $K\times F$ 阶矩阵 $C$ 的第k行，对角元素为 $c_{kf}$ 。为了在最小二乘中拟合模型，应该最小化损失函数，如下所示：

$\sigma ={\displaystyle \underset{k=1}{\overset{K}{\sum }}{\Vert {\chi }_k-A{D}_k{B}^{\text{T}}\Vert }_F^2}$ (15)

3.2. 模型的唯一性分析

PARAFAC模型具有模糊性问题，即不确定性问题，具体就是排列模糊和尺度模糊问题 [3] 。对于上一小节中的三阶张量 $\chi$ 和因子矩阵 $A$ 、 $B$ 和 $C$ ，排列模糊问题 [2] 具体如下式所示：

$\chi =〚A,B,C〛=〚A\Pi ,B\Pi ,C\Pi 〛$ (16)

其中 $〚·〛$ 表示多线性乘积， $\Pi$ 表示 $F\times F$ 列交换矩阵， $A=\left[a_1,a_2,\cdots ,a{}_F\right]$ ， $B=\left[b_1,b_2,\cdots ,b{}_F\right]$ ， $C=\left[c_1,c_2,\cdots ,c{}_F\right]$ 。

尺度模糊问题 [2] 为：当满足 ${\alpha }_f{\beta }_f{\gamma }_f=1,\forall f=1,\cdots ,F$ ，即

$\chi ={\displaystyle \underset{f=1}{\overset{F}{\sum }}\left({\alpha }_f{a}_f\right)\circ \left({\beta }_f{b}_f\right)}\circ \left({\gamma }_f{c}_f\right)={\displaystyle \underset{f=1}{\overset{F}{\sum }}{a}_f\circ b_f\circ c_f}$ (17)

针对PARAFAC模型的排列模糊和尺度模糊问题，Kruskal在1977年提出了PARAFAC模型唯一性分解的充分条件 [17] ：

$k_A+k_B+k_C\ge 2F+2$ (18)

其中 $F$ 表示三个因子矩阵的列向量数。满足式(17)的时候，张量分解唯一，此时只存在排列模糊和尺度模糊问题。排列模糊和尺度模糊表示如下所示：

$\bar{A}=A\Pi {\Delta }_1,\bar{B}=B\Pi {\Delta }_2,\bar{C}=C\Pi {\Delta }_3$ (19)

其中 $\Pi \in {ℂ}^{F\times F}$ 为列交换矩阵， ${\Delta }_i\in {ℂ}^{F\times F}\left(i=1,2,3\right)$ 表示对角模糊矩阵，并且满足 ${\Delta }_1{\Delta }_2{\Delta }_3=I_F$ 。

在2.1中介绍如果由列向量构成的矩阵 $A\in {ℂ}^{I\times J}$ ，并且这些列向量是从绝对连续分布中独立提取出的元素，因此矩阵不仅满秩而且满足k-秩。矩阵 $A$ 、 $B$ 和 $C$ 的列向量是从绝对连续分布中独立提取的元素，式(17)就可以写成：

$\min \left(I,F\right)+\min \left(J,F\right)+\min \left(K,F\right)\ge 2F+2$ (20)

由式(19)可知：PARAFAC模型可以通过调整因子矩阵的行数来使其分解唯一。在实际应用的场景中就可以改变系统的相关参数来使模型分解唯一。

4. 模型的求解

PARAFAC模型最传统的求解方式是三线性交替最小二乘算法(Trilinear Alternating Least Square, TALS)。它的基本原理是首先更新一个矩阵，然后对其余的矩阵进行最小二乘算法进行更新，如此迭代更新矩阵直到收敛，最终算法结束。由于TALS算法的缺陷是要花费大量的时间来计算，因此本文主要借助一种提高TALS收敛速度的算法来对PARAFAC模型进行求解，称为COMFAC (Complex Parallel Factor Analysis)算法 [7] 。该算法的原理框架如图2所示。

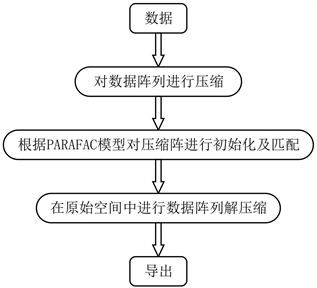
Figure 2. COMFAC algorithm flowchart

图2. COMFAC算法流程图

首先是对数据阵列进行压缩。数据阵为三阶张量 $\chi \in {ℂ}^{I\times J\times K}$ ，分别在这三个维度上新定义三个压缩矩阵 $U\left(I\times P\right)$ 、 $V\left(J\times Q\right)$ 、 $Z\left(K\times R\right)$ ，值得注意的是 $P\le I,Q\le J,R\le K$ 。因此，三阶张量 $\chi$ 被压缩成 $G\left(P\times Q\times R\right)$ 。在压缩过程中使用的是Tucker3-ALS算法，它的步骤如图3所示。

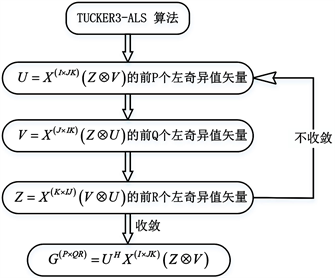
Figure 3. Tucker3-ALS algorithm flowchart

图3. Tucker3-ALS算法流程图

根据 $G^{\left(P\times QR\right)}=U^H{X}^{\left(I\times JK\right)}\left(Z\otimes V\right)$ 可知，只需要进行矩阵的逆变换就可以得到原始矩阵 $X^{\left(I\times JK\right)}$ ，即

${\hat{X}}^{\left(I\times JK\right)}=U{G}^{\left(P\times QR\right)}\left(Z^H\otimes V^H\right)$ (21)

对数据进行压缩之后，接着对矩阵 $G$ 的PARAFAC模型进行初始化，主要是对 $G^{\left(P\times QR\right)}$ 、 $G^{\left(Q\times RP\right)}$ 、 $G^{\left(R\times PQ\right)}$ 进行奇异值分解。

PARAFAC模型是从三个不同的维度来展开数据阵，经过压缩后的矩阵 $G$ 可以表示为：

$G_r=L{D}_r\left(N\right)M^{\text{T}}+E_r,r=1,\cdots ,R$ (22)

其中 $L\left(P\times F\right)$ 、 $M\left(Q\times F\right)$ 、 $N\left(R\times F\right)$ 。 $F$ 表示经过奇异值分解之后取得前 $F$ 个左奇异值矢量，即因子的个数。 $E_r$ 表示误差矩阵。在PARAFAC模型的框架下，三阶张量可以重构成二维矩阵形式。同样在COMFAC分解中，压缩阵 $G$ 可以表示为：

${\hat{G}}^{\left(P\times QR\right)}=L{\left(N\odot M\right)}^{\text{T}}$ (23)

等价于：

${\hat{G}}^{\left(P\times QR\right)}=L{\left(N^{*}\odot M^{*}\right)}^H$ (24)

为了简化计算，忽略矩阵上标，将(24)代入(21)中，得到：

${\hat{X}}^{\left(I\times JK\right)}=U{G}^{\left(P\times QR\right)}\left(Z^H\otimes V^H\right)\approx UL{\left(N^{*}\odot M^{*}\right)}^H{\left(Z\otimes V\right)}^H=UL{\left[\left(Z\otimes V\right)\left(N^{*}\odot M^{*}\right)\right]}^H$ (25)

根据运算性质(10)可得

${\hat{X}}^{\left(I\times JK\right)}\approx UL{\left[\left(Z\otimes V\right)\left(N^{*}\odot M^{*}\right)\right]}^H=UL{\left(Z{N}^{*}\odot V{M}^{*}\right)}^H=UL{\left(Z^{*}N\odot V^{*}M\right)}^H$ (26)

定义 $A\approx UL,B\approx V^{*}M,C\approx Z^{*}N$ ，最终得到

${\hat{X}}^{\left(I\times JK\right)}\approx A{\left(C\odot B\right)}^{\text{T}}$ (27)

最后再根据实际应用背景来计算误码率大小。

5. 应用

本文只考虑上行DS-CDMA系统，其中用户数量 $F=6$ ，传输的数据是采用随机二进制相移键控(Binary Phase Shift Keying, BPSK)符号，扩频码长度为 $K=4$ ，符号快照的块长度为 $J=50$ 。在观测接收到张量 $\chi \in {ℂ}^{I\times 50\times 4}$ 后，首先加入不同信噪比条件下的高斯白噪声，其次进行模糊去除，接着执行COMFAC算法来对DS-CDMA系统进行盲数据检测。它们的性能通过误码率(Bit Error Rate, BER)来体现，这是通过平均1000次蒙特卡洛独立实验得到的平均值。最后，本文在相同的信噪比条件下，得到天线根数范围取4到20对应的误码率，这是由于根据PARAFAC模型的唯一性可知天线根数至少为4，否则误码率的大小脱离实际意义。在此基础上将误码率与天线根数进行数据拟合，取合适的拟合方式，拟合函数中最小的极小值点进行四舍五入得到不同信噪比条件下的最优天线的根数。如图4和图5所示是信噪比1~30条件下误码率与天线根数的拟合曲线。拟合函数如式(28)~(57)，具体见附录。

(a) (b) (c) (d) (e) (f) (g) (h) (i) (j) (k) (l) (m) (n)

Figure 4. Fit the function curve picture. (a) SNR = 1; (b) SNR = 2; (c) SNR = 3; (d) SNR = 4; (e) SNR = 5; (f) SNR = 6; (g) SNR = 7; (h) SNR = 8; (i) SNR = 9; (j) SNR = 10; (k) SNR = 11; (l) SNR = 12; (m) SNR = 13; (n) SNR = 14

图4. 拟合函数曲线图。(a) SNR = 1; (b) SNR = 2; (c) SNR = 3; (d) SNR = 4; (e) SNR = 5; (f) SNR = 6; (g) SNR = 7; (h) SNR = 8; (i) SNR = 9; (j) SNR = 10; (k) SNR = 11; (l) SNR = 12; (m) SNR = 13; (n) SNR = 14

(a) (b) (c) (d) (e) (f) (g) (h) (i) (j) (k) (l) (m) (n) (o) (p)

Figure 5. Fit the function curve picture. (a) SNR = 15; (b) SNR = 16; (c) SNR = 17; (d) SNR = 18; (e) SNR = 19; (f) SNR = 20; (g) SNR = 21; (h) SNR = 22; (i) SNR = 23; (j) SNR = 24; (k) SNR = 25; (l) SNR = 26; (m) SNR = 27; (n) SNR = 28; (o) SNR = 29; (p) SNR = 30

图5. 拟合函数曲线图。(a) SNR = 15; (b) SNR = 16; (c) SNR = 17; (d) SNR = 18; (e) SNR = 19; (f) SNR = 20; (g) SNR = 21; (h) SNR = 22; (i) SNR = 23; (j) SNR = 24; (k) SNR = 25; (l) SNR = 26; (m) SNR = 27; (n) SNR = 28; (o) SNR = 29; (p) SNR = 30

通过观察拟合曲线并且结合拟合方程来求函数的最小的极小值点，结合实际意义进行四舍五入，得到结果如表1所示。通过观察结果可知拟合方式主要有三种：Sum of Sine、Fourier、Polynomial。它们的拟合优度都达到90%以上，高信噪比的最优天线数少，并且比较稳定；低信噪比的最优天线数多，并且随着信噪比变低，它的最优天线数量不稳定；当信噪比为负数的时候，误码率趋于稳定的速度非常慢进而导致研究最优天线数失去实际意义。

Table 1. Optimal antenna statistics table

表1. 最优天线统计表

6. 结论与研究展望

6.1. 总结

本文在DS-CDMA系统中基于张量分解技术建立PARAFAC模型，固定用户数量、扩频码数、符号快照的块长度数，改变信噪比和天线数量，接着执行COMFAC算法得出误码率，将误码率与天线数量进行数据拟合，最后观察拟合函数曲线和拟合方程得出最优天线数。根据蒙特卡洛模拟和数据拟合发现拟合方式主要有三种：Sum of Sine、Fourier、Polynomial，同时拟合优度都在90%以上。此外，最优天线受信噪比的影响，高信噪比的最优天线数少，并且稳定为5根天线；低信噪比的最优天线数多，并且随着信噪比变低，它的最优天线数量不稳定；当信噪比为负数的时候，误码率趋于稳定的速度非常慢，得到的结果也失去研究意义。

6.2. 研究展望

第一，本文并没有考虑负信噪比，因为误码率趋于稳定的速度非常慢，甚至误码率的大小一直脱离实际意义，这是受算法的影响。虽然PARAFAC模型只是张量分解的一种形式，执行COMFAC算法的时候虽然极大提高了运算时间，但是算法精度和收敛速度可以进一步提高。

第二，本文只是取的离散的正整数信噪比，此外信噪比为负数的时候并没有考虑。因此，如果信噪比范围扩大，并且是连续的情况，最优天线的数量可以进一步深入研究。

第三，本文只是在DS-CDMA系统中固定用户数量、扩频码数、符号快照的块长度数来进行仿真模拟，实际生活中的问题更加复杂，误码率和用户、扩频码、天线数量等的其他函数关系可以进一步研究，甚至误码率的其他影响因素也是不容忽视的。

未来的工作聚焦于上述三点，并且模型和算法的优化更是研究的重点。

附录

当 $SNR=1$ 的时候，拟合函数：

$\begin{array}{l}f\left(x\right)=2.2\sin \left(\text{0}\text{.05336}x+\text{2}\text{.301}\right)+\text{0}\text{.566}\sin \left(\text{0}\text{.2253}x+\text{2}\text{.961}\right)\\ \begin{array}{ccc}& & +\text{0}\text{.05511}\sin \left(\text{0}\text{.6263}x+\text{0}\text{.7143}\right)+\text{0}\text{.01604}\sin \left(\text{0}\text{.9226}x+\text{0}\text{.3011}\right)\end{array}\end{array}$ (28)

当 $SNR=2$ 的时候，拟合函数：

$\begin{array}{l}f\left(x\right)=\text{1}\text{.339}\sin \left(\text{0}\text{.07806}x+\text{1}\text{.954}\right)+\text{0}\text{.4957}\sin \left(\text{0}\text{.2684}x+\text{2}\text{.444}\right)\\ \begin{array}{ccc}& & +\text{0}\text{.1126}\sin (\text{0}\text{.6023}x+\text{1}\text{.19})+\text{0}\text{.03626}\sin \left(\text{0}\text{.7287}x+\text{2}\text{.934}\right)\end{array}\end{array}$ (29)

当 $SNR=3$ 的时候，拟合函数：

$\begin{array}{l}f\left(x\right)=-\text{4}\text{.996}\times {\text{10}}^7+\text{6}\text{.089}\times {\text{10}}^7\cos \left(\text{0}\text{.06478}x\right)+\text{6}\text{.092}\times {\text{10}}^7\sin \left(\text{0}\text{.06478}x\right)+\text{3}\text{.208}\times {\text{10}}^4\cos \left(0.12956x\right)\\ \begin{array}{ccc}& & -\text{5}\text{.475}\times {\text{10}}^7\sin \left(0.12956x\right)-\text{1}\text{.771}\times {\text{10}}^7\cos \left(0.19434x\right)+\text{1}\text{.768}\times {\text{10}}^7\sin \left(0.19434x\right)\end{array}\\ \begin{array}{ccc}& & +\text{7}\text{.811}\times {\text{10}}^6\cos \left(0.25912x\right)+\text{1}\text{.221}\times {\text{10}}^4\sin \left(0.25912x\right)-\text{1}\text{.054}\times {\text{10}}^6\cos \left(0.3239x\right)\end{array}\\ \begin{array}{ccc}& & -\text{1}\text{.059}\times {\text{10}}^6\sin \left(0.3239x\right)-\text{446}\text{.2}\cos \left(0.38868x\right)+\text{1}\text{.326}\times {\text{10}}^5\sin \left(0.38868x\right)\end{array}\end{array}$ (30)

当 $SNR=4$ 的时候，拟合函数：

$\begin{array}{l}f\left(x\right)=\text{0}\text{.4534sin}\left(\text{0}\text{.1701}x+0.6735\right)+\text{0}\text{.3187}\sin \left(0.3531x+1.392\right)+\text{0}\text{.09555sin}\left(\text{0}\text{.6825}x+\text{0}\text{.2507}\right)\\ \begin{array}{ccc}& & +0.0409\sin \left(1.005x-0.4421\right)-\end{array}\text{0}\text{.01361}\sin \left(1.005x+6.941\right)\end{array}$ (31)

当 $SNR=5$ 的时候，拟合函数：

$f\left(x\right)=5.764\times {10}^5{x}^4-\text{0}\text{.003194}{x}^3+\text{0}\text{.0646}{x}^2-\text{0}\text{.5679}x+1.875$ (32)

当 $SNR=6$ 的时候，拟合函数：

$\begin{array}{l}f\left(x\right)=\text{0}\text{.5778sin}\left(\text{0}\text{.09163}x+\text{1}\text{.849}\right)+\text{0}\text{.2456}\sin \left(\text{0}\text{.2606}x+\text{2}\text{.728}\right)+\text{0}\text{.03345sin}\left(\text{0}\text{.7272}x-0.1952\right)\\ \begin{array}{ccc}& & +\text{0}\text{.01825}\sin \left(1.113x-1.875\right)+\end{array}\text{0}\text{.01142}\sin \left(1.515x+2.316\right)\end{array}$ (33)

当 $SNR=7$ 的时候，拟合函数：

$f\left(x\right)=-\text{6}\text{.33}\times {\text{10}}^6{x}^5+\text{0}\text{.0004268}{x}^4-\text{0}\text{.01117}{x}^3+\text{0}\text{.1417}{x}^2-0.8734x+2.129$ (34)

当 $SNR=8$ 的时候，拟合函数：

$f\left(x\right)=-\text{5}\text{.929}\times {\text{10}}^6{x}^5+\text{0}\text{.0003952}{x}^4-\text{0}\text{.01023}{x}^3+\text{0}\text{.1284}{x}^2-0.7818x+1.87$ (35)

当 $SNR=9$ 的时候，拟合函数：

$f\left(x\right)=-5.849\times {\text{10}}^6{x}^5+\text{0}\text{.0003867}{x}^4-\text{0}\text{.009888}{x}^3+\text{0}\text{.1219}{x}^2-\text{0}\text{.7239}x+1.674$ (36)

当 $SNR=10$ 的时候，拟合函数：

$f\left(x\right)=-3.964\times {\text{10}}^6{x}^5+\text{0}\text{.0002663}{x}^4-\text{0}\text{.006922}{x}^3+\text{0}\text{.08681}{x}^2-\text{0}\text{.5246}x+1.233$ (37)

当 $SNR=11$ 的时候，拟合函数：

$\begin{array}{l}f\left(x\right)=28.31+12.82\cos \left(0.1453x\right)-46.96\sin \left(0.1453x\right)-26.39\cos \left(0.2906x\right)\\ \begin{array}{cc}\begin{array}{cc}& \end{array}& -15.53\sin \left(0.2906x\right)-9.681\cos \left(0.4359x\right)+9.471\sin \left(0.4359x\right)+1.872\cos \left(0.5812x\right)\end{array}\\ \begin{array}{cc}\begin{array}{cc}& \end{array}& +3.344\sin \left(0.5812x\right)+0.5181\cos \left(0.7265x\right)\end{array}-0.1295\sin \left(0.7265x\right)\end{array}$ (38)

当 $SNR=12$ 的时候，拟合函数：

$f\left(x\right)=-2.726\times {10}^6{x}^5+0.0001795x^4-0.004573x^3+0.05625x^2-0.3339x+0.7746$ (39)

当 $SNR=13$ 的时候，拟合函数：

$\begin{array}{l}f\left(x\right)=1.152\times {10}^5-1.365\times {10}^5\cos \left(0.06289x\right)-1.367\times {10}^5\sin \left(0.06289x\right)\\ \begin{array}{ccc}& & -132.9\cos \left(0.12578x\right)+1.124\times {10}^5\sin \left(0.12578x\right)+3.082\times {10}^4\cos \left(0.18867x\right)\end{array}\\ \begin{array}{ccc}& & -3.07\times {10}^4\sin \left(0.18867x\right)-1.01\times {10}^4\cos \left(0.25156x\right)-31.63\sin \left(0.25156x\right)\end{array}\\ \begin{array}{ccc}& & +752.6\cos \left(0.31445x\right)+759.8\sin \left(0.31445x\right)\end{array}\end{array}$ (40)

当 $SNR=14$ 的时候，拟合函数：

$\begin{array}{l}f\left(x\right)=6.435\times {10}^7-9.798\times {10}^7\cos (0.03191x)-4.414\times {10}^7\sin \left(0.03191x\right)\\ \begin{array}{ccc}& & +4.093\times {10}^7\cos \left(0.06328x\right)+4.626\times {10}^7\sin \left(0.06328x\right)-6.937\times {10}^6\cos \left(0.09573x\right)\end{array}\\ \begin{array}{ccc}& & -2.234\times {10}^7\sin \left(0.09573x\right)-6.423\times {10}^5\cos \left(0.12764x\right)+5.231\times {10}^6\sin \left(0.12764x\right)\end{array}\\ \begin{array}{ccc}& & +2.783\times {10}^5\cos \left(0.15955x\right)-4.586\times {10}^5\sin \left(0.15955x\right)\end{array}\end{array}$ (41)

当 $SNR=15$ 的时候，拟合函数：

$f\left(x\right)=-1.887\times {10}^6{x}^5+0.0001242x^4-0.003164x^3+0.0389x^2-0.2308x+0.5362$ (42)

当 $SNR=16$ 的时候，拟合函数：

$f\left(x\right)=-1.642\times {10}^{-6}{x}^5+\text{0}\text{.0001063}{x}^4-\text{0}\text{.002663}{x}^3+0.03217x^2-0.1872x+0.4248$ (43)

当 $SNR=17$ 的时候，拟合函数：

$\begin{array}{l}f\left(x\right)=0.02813\sin \left(0.1876x+0.4112\right)+0.02047\sin \left(0.3674x+1.265\right)\\ \begin{array}{ccc}& & +0.006501\sin \left(0.7457x-0.3742\right)+0.002799\sin \left(1.13x-2.269\right)\end{array}\\ \begin{array}{ccc}& & +0.001412\sin \left(1.559x+1.482\right)\end{array}\end{array}$ (44)

当 $SNR=18$ 的时候，拟合函数：

$\begin{array}{l}f\left(x\right)=0.03523\sin \left(0.1878x+0.4974\right)+0.02679\sin \left(0.3489x+1.561\right)\\ \begin{array}{ccc}& & \begin{array}{l}+0.007204\sin \left(0.7176x+0.03323\right)+0.003803\sin \left(1.128x-2.043\right)\\ +0.002173\sin \left(1.52x+2.349\right)\end{array}\end{array}\end{array}$ (45)

当 $SNR=19$ 的时候，拟合函数：

$\begin{array}{l}f\left(x\right)=0.04125\sin \left(0.1882x+0.4663\right)+0.03123\sin \left(0.3094x+2.039\right)\\ \begin{array}{ccc}& & +0.004423\sin \left(0.7486x-0.3983\right)+0.003346\sin \left(1.149x-2.535\right)\end{array}\end{array}$ (46)

当 $SNR=20$ 的时候，拟合函数：

$\begin{array}{l}f\left(x\right)=0.02564\sin \left(0.1882x+0.4662\right)+0.01854\sin \left(0.3717x+1.237\right)\\ \begin{array}{ccc}& & +0.006017\sin \left(0.7566x-0.5913\right)+0.002827\sin \left(1.164x-2.798\right)\end{array}\\ \begin{array}{ccc}& & +0.00291\sin \left(2.754x-2.592\right)\end{array}\end{array}$ (47)

当 $SNR=21$ 的时候，拟合函数：

$\begin{array}{l}f\left(x\right)=0.02624\sin \left(0.1879x+0.5108\right)+0.01972\sin \left(0.3379x+1.681\right)\\ \begin{array}{ccc}& & +0.004308\sin \left(0.7513x-0.5372\right)+0.002093\sin \left(1.125x-2.107\right)\end{array}\\ \begin{array}{ccc}& & +0.001628\sin \left(1.523x+1.908\right)\end{array}\end{array}$ (48)

当 $SNR=22$ 的时候，拟合函数：

$\begin{array}{l}f\left(x\right)=7.571\times {10}^6-8.988\times {10}^6\cos \left(0.06542x\right)-9.463\times {10}^6\sin \left(0.06542x\right)-4.272\times {10}^5\cos \left(0.13084x\right)\\ \begin{array}{ccc}& & +8.283\times {10}^6\sin \left(0.13084x\right)+2.88\times {10}^6\cos \left(0.19626x\right)-2.465\times {10}^6\sin \left(0.19626x\right)\end{array}\\ \begin{array}{ccc}& & -1.176\times {10}^6\cos \left(0.26168x\right)-1.225\times {10}^5\sin \left(0.26168x\right)+1.378\times {10}^5\cos \left(0.3271x\right)\end{array}\\ \begin{array}{ccc}& & +1.794\times {10}^5\sin \left(0.3271x\right)+3147\cos \left(0.39252x\right)-1.981\times {10}^4\sin \left(0.39252x\right)\end{array}\end{array}$ (49)

当 $SNR=23$ 的时候，拟合函数：

$\begin{array}{l}f\left(x\right)=1.466\times {10}^7-1.775\times {10}^7\cos \left(0.0651x\right)-1.799\times {10}^7\sin \left(0.0651x\right)-2.138\times {10}^5\cos \left(0.1302x\right)\\ \begin{array}{ccc}& & +1.605\times {10}^7\sin \left(0.1302x\right)+5.288\times {10}^6\cos \left(0.1953x\right)-5.08\times {10}^6\sin \left(0.1953x\right)\end{array}\\ \begin{array}{ccc}& & -2.285\times {10}^6\sin \left(0.1953x\right)-6.167\times {10}^4\sin \left(0.2604x\right)+2.981\times {10}^5\cos \left(0.3255x\right)\end{array}\\ \begin{array}{ccc}& & +3.191\times {10}^5\sin \left(0.3255x\right)+1599\cos \left(0.3906x\right)-3.863\times {10}^4\sin \left(0.3906x\right)\end{array}\end{array}$ (50)

当 $SNR=24$ 的时候，拟合函数：

$\begin{array}{l}f\left(x\right)=6.969\times {10}^6-8.415\times {10}^6\sin \left(0.06514x\right)-8.572\times {10}^6\sin \left(0.06514x\right)-1.408\times {10}^5\cos \left(0.13028x\right)\\ \begin{array}{ccc}& & +7.631\times {10}^6\sin \left(0.13028x\right)+2.533\times {10}^6\cos \left(0.19542x\right)-2.396\times {10}^6\sin \left(0.19542x\right)\end{array}\\ \begin{array}{ccc}& & -1.087\times {10}^6\cos \left(0.26056x\right)-4.07\times {10}^4\sin \left(0.26056x\right)+1.398\times {10}^5\cos \left(0.3257x\right)\end{array}\\ \begin{array}{ccc}& & +1.537\times {10}^5\sin \left(0.3257x\right)+1059\cos \left(0.39084x\right)-1.838\times {10}^4\sin \left(0.39084x\right)\end{array}\end{array}$ (51)

当 $SNR=25$ 的时候，拟合函数：

$\begin{array}{l}f\left(x\right)=1.937\times {10}^6-2.307\times {10}^6\cos \left(0.06545x\right)-2.414\times {10}^6\sin \left(0.06545x\right)-9.6014\times {10}^4\cos \left(0.1309x\right)\\ \begin{array}{ccc}& & +2.118\times {10}^6\sin \left(0.1309x\right)+7.291\times {10}^5\cos \left(0.19635x\right)-6.359\times {10}^5\sin \left(0.19635x\right)\end{array}\\ \begin{array}{ccc}& & -3\times {10}^5\cos \left(0.2618x\right)-2.746\times {10}^4\sin \left(0.2618x\right)+3.57\times {10}^4\cos \left(0.32725x\right)\end{array}\\ \begin{array}{ccc}& & +4.5\times {10}^4\sin \left(0.32725x\right)+701.5\cos \left(0.3927x\right)-5026\sin \left(0.3927x\right)\end{array}\end{array}$ (52)

当 $SNR=26$ 的时候，拟合函数：

$\begin{array}{l}f\left(x\right)=6.829\times {10}^6-8.184\times {10}^6\cos \left(0.0649x\right)-8.458\times {10}^6\sin \left(0.0649x\right)-2.469\times {10}^5\cos \left(0.1298x\right)\\ \begin{array}{ccc}& & +7.47\times {10}^6\sin \left(0.1298x\right)+2.529\times {10}^6\cos \left(0.1947x\right)-2.289\times {10}^6\sin \left(0.1947x\right)\end{array}\\ \begin{array}{ccc}& & -1.06\times {10}^6\sin \left(0.2596x\right)-7.096\times {10}^4\sin \left(0.2596x\right)+1.306\times {10}^5\cos \left(0.3245x\right)\end{array}\\ \begin{array}{ccc}& & +1.548\times {10}^5\sin \left(0.3245x\right)+1828\cos \left(0.3894x\right)-1.78\times {10}^4\sin \left(0.3894x\right)\end{array}\end{array}$ (53)

当 $SNR=27$ 的时候，拟合函数：

$\begin{array}{l}f\left(x\right)=4.4\times {10}^6-5.23\times {10}^6\cos \left(0.065x\right)-5.489\times {10}^6\sin \left(0.065x\right)-2.332\times {10}^5\cos \left(0.13x\right)\\ \begin{array}{ccc}& & +4.809\times {10}^6\sin \left(0.13x\right)+1.662\times {10}^6\cos \left(0.195x\right)-1.436\times {10}^6\sin \left(0.195x\right)\end{array}\\ \begin{array}{ccc}& & -6.805\times {10}^5\cos \left(0.26x\right)-6.679\times {10}^4\sin \left(0.26x\right)+8.016\times {10}^4\cos \left(0.325x\right)\end{array}\\ \begin{array}{ccc}& & +1.028\times {10}^5\sin \left(0.325x\right)+1711\cos \left(0.39x\right)-1.139\times {10}^4\sin \left(0.39x\right)\end{array}\end{array}$ (54)

当 $SNR=28$ 的时候，拟合函数：

$\begin{array}{l}f\left(x\right)=9.601\times {10}^6-1.146\times {10}^7\cos \left(0.06537x\right)-1.193\times {10}^7\sin \left(0.06537x\right)-425600\cos \left(0.13074x\right)\\ \begin{array}{ccc}& & +1.05\times {10}^7\sin \left(0.13074x\right)+3.595\times {10}^6\cos \left(0.19611x\right)-3.181\times {10}^6\sin \left(0.19611x\right)\end{array}\\ \begin{array}{ccc}& & -1.491\times {10}^6\cos \left(0.26148x\right)-1.22\times {10}^5\sin \left(0.26148x\right)+1.802\times {10}^5\cos \left(0.32685x\right)\end{array}\\ \begin{array}{ccc}& & +2.216\times {10}^5\sin \left(0.32685x\right)\end{array}+3131\cos \left(0.39222x\right)-2.508\times {10}^4\sin \left(0.39222x\right)\end{array}$ (55)

当 $SNR=29$ 的时候，拟合函数：

$\begin{array}{l}f\left(x\right)=5.7\times {10}^6-6.854\times {10}^6\cos \left(0.06525x\right)-7.038\times {10}^6\sin \left(0.06525x\right)-1.662\times {10}^5\cos \left(0.1305x\right)\\ \begin{array}{ccc}& & +6.237\times {10}^6\sin \left(0.1305x\right)+2.093\times {10}^6\cos \left(0.19575x\right)-1.931\times {10}^6\sin \left(0.19575x\right)\end{array}\\ \begin{array}{ccc}& & -8.856\times {10}^5\cos \left(0.261x\right)-4.767\times {10}^4\sin \left(0.261x\right)+1.113\times {10}^5\cos (0.32625x)\end{array}\\ \begin{array}{ccc}& & +1.275\times {10}^5\sin \left(0.32625x\right)+1224\cos \left(0.3915x\right)-1.491\times {10}^4\sin \left(0.3915x\right)\end{array}\end{array}$ (56)

当 $SNR=30$ 的时候，拟合函数：

$\begin{array}{l}f\left(x\right)=3.044\times {10}^6-3.592\times {10}^6\cos \left(0.0654x\right)-3.825\times {10}^6\sin \left(0.0654x\right)-2.09\times {10}^5\cos \left(0.1308x\right)\\ \begin{array}{ccc}& & +3.327\times {10}^6\sin \left(0.1308x\right)+1.174\times {10}^6\cos \left(0.1962x\right)-9.705\times {10}^5\sin \left(0.1962x\right)\end{array}\\ \begin{array}{ccc}& & -4.71\times {10}^5\cos \left(0.2616x\right)-5.994\times {10}^4\sin \left(0.2616x\right)+5.316\times {10}^4\cos \left(0.327x\right)\end{array}\\ \begin{array}{ccc}& & +7.351\times {10}^4\sin \left(0.327x\right)+1539\cos \left(0.3924x\right)-7885\sin \left(0.3924x\right)\end{array}\end{array}$ (57)