面向天地一体化网络的路由架构设计

Design of Routing Architecture for Integrated Network of Sky and Earth

摘要: 随着天地一体化网络快速发展，传统路由架构已无法满足当今多业务传输需求。天地一体化网络存在星间链路拥塞和流量分布不均等问题。为了满足多业务传输需求，为用户提供快速高效的路径传输服务。本文针对上述问题，提出解决方案，首先，本文引入了SDN结合SR的部署方案，控制层面通过控制器计算路由，数据平面使用分段路由(SR)指导数据转发。旨在空间网络中提供可靠传输服务，减少路由条目。然后，本文基于传统路径搜索算法进行改进提出了一种路由计算方法TPSR，包括路径选择算法和路径搜索算法，在数据到来时能够快速搜索一条最优路径。最后，本文采用了Ryu和Mininet等开源工具对路由架构进行实现，并进行了多组实验验证其性能和有效性。对实验结果进行分析和总结，该路由架构在提高空间网络性能方面的显著效果。

Abstract: With the rapid development of the integrated network of sky and earth, traditional routing architectures can no longer meet the demands of modern multi-service transmission. Problems such as inter-satellite link congestion and uneven traffic distribution exist in the integrated network of sky and earth. In order to provide users with fast, efficient, and reliable path transmission services to meet the demands of multi-service transmission, this paper proposes a solution to the aforementioned issues. Firstly, this paper introduces an SDN combined with SR deployment scheme, in which the control plane calculates routing via a controller and the data plane uses Segment Routing (SR) to guide data forwarding. The aim is to provide reliable transmission services in the spatial network while reducing routing entries. Secondly, this paper proposes an improved path calculation algorithm TPSR based on traditional path searching algorithms, including path selection algorithm and path search algorithm, which can quickly search for an optimal path when data arrives. Finally, the routing architecture is implemented using open-source tools such as Ryu and Mininet, and multiple experiments are conducted to verify its performance and effectiveness. The experimental results are analyzed and summarized, demonstrating the significant improvement of this routing architecture in enhancing space network performance.

1. 引言

在天地一体化网络体系中，软件定义网络(SDN)技术广泛应用在网络负载均衡、流量工程等领域 [1] ，但在空间网络中引入SDN技术存在严峻的挑战 [2] 。由于空间网络拓扑频繁变化、卫星资源受限，现有SDN路由方法在数据层面存在流表项过多、流表下发过慢，链路易拥塞等情况 [3] [4] 。为了减少数据层面的信息规模，提高转发效率，需要一种解决方案让SDN技术能够应用于空间网络，减小流表项规模，进而缓解设备资源压力。SR [5] 采用源路由技术，在数据层面无状态转发的特性使其广泛应用于SDN网络、流量工程等领域。因此，如果将SDN结合SR技术应用于空间网络中，可以为用户提供更为精确、稳定、高可靠性的传输服务，同时减少数据层面流表项。此外，当一体化网络热点流量分布不均，局部链路业务流量过多时，传统的SDN路由方法往往难以满足实际需求，容易出现局部链路拥塞和转发节点丢包的情况。本文聚焦于实现网络带宽资源的有效利用的目标，通过对链路状态进行评估来计算最优路径，进而降低链路拥塞对数据传输的影响。综上，设计一种面向天地一体化网络的SDN路由架构具有重要意义。天地一体化网络架构如图1所示。

2. 相关工作

近年来，相关研究学者提出了许多用于一体化网络的路由方案。Alidadi等人 [6] 提出了一种基于SDN-MPLS的具有较低计算复杂度的算法PSLC。PSLC算法改进了带宽限制路由，因为它在移动网络中的网络负载平衡、路径长度、节能和低复杂性之间进行了权衡。Varyani等人 [7] 提出了一种基于QoS的路由方案(QROUTE)。QROUTE满足软件定义覆盖网络中的多个QoS约束。传统路由算法由于路由计算时间长，无法适应快速变化的覆盖链路QoS特性。QROUTE还通过减少数据平面中的转发条目来节省转发元素的存储空间。Gong等人 [8] 提出了一种模糊延迟带宽保证路由(FDBGR)算法，该算法同时考虑了路由中的延迟和带宽约束。所提出的模糊系统基于可以推迟具有高资源需求的请求的规则。结果表明在视频会议应用中FDBGR可以有效降低时延。Casas-Velasco等人 [9] 开发了一种用于SDN中路由的深度强化学习(DRL)方法。由于传统路由协议在做出路由决策的过程中使用了非常狭窄的信息，导致在路由路径选择过程中缺乏(或缓慢)适应流量变化并涉及QoS指标，作者提出了深度强化学习软件定义网络智能路由(DRSIR)机制。采用DRL是因为经典的基于强化学习的解决方案在处理大型动作和状态空间时通常会遇到存储和时间挑战。DRSIR 考虑路径状态指标，以能够适应动态流量变化的方式提供主动、高效、有弹性和智能的路由。

综上所述，已有面向一体化网络路由的研究主要针对控制层面路由算法进行优化，但机制较为复杂、计算开销较高，存在一定的优化空间。对于数据层面路由条目过多的问题，优化程度尚有不足。对空间网络适用性不佳。因此，本文提出了一种面向天地一体化网络的SDN路由架构。在优化路由计算机制的同时，有效降低数据层面流表项过多的问题。

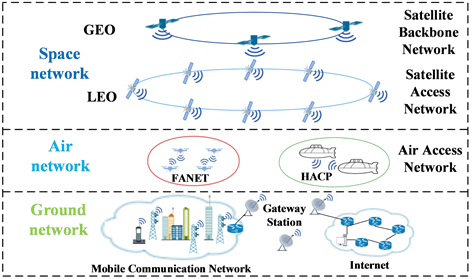
Figure 1. Integrated network architecture of sky and earth

图1. 天地一体化网络架构

3. 系统设计

本文提出的面向天地一体化网络的SDN路由架构主要是基于SDN的路由控制机制，并利用虚拟网络拓扑结构中的网络拓扑信息和SDN控制器中的路由计算方法，实现数据包的快速转发和动态路由调整。图2详细介绍该架构的工作流程。

首先，聚焦于提高业务传输路径服务质量的目标，本文使用随机K最短路径算法计算出n条的最短路径。由于链路的最小剩余带宽、最大时延、最大丢包率等指标反应链路的综合状态。因此，在选择最优路径时，应该综合考虑路径上各个链路的指标，选择稳定、剩余带宽尽量大、时延尽量小、丢包率尽量低的路径。最终获得最优路径。

其次，在空间网络中，为了减少数据层面流表项数目，本文在数据层面使用SR指导数据在空间网络中转发，利用SR源路由思想以及无状态转发的特性，可以大幅减少流表项，减轻空间网络负担，指导数据完成路径转发，最终实现快速高效的最优路径传输。

本文将SDN结合SR的部署方案引入到空间网络中，可以显著地减少空间网络设备所维持的路由表项数目。经过分析和研究，此种部署方案可行性较高，可以作为有效承担空间网络数据转发的一种方式。

在此基础上，本文提出了适用于天地一体化网络的路由方案TPSR，在控制层面使用SDN控制器进行拓扑信息监测，评估链路状态，综合计算最优转发路径。在数据层面使用SR技术指导数据包转发，将转发路径的信息在路径节点压入SL，中间节点按SL标签进行转发。这样既符合现有的SDN网络体系结构，又可缓解数据平面的下发表项数量过多的问题。

Figure 2. TPSR system architecture

图2. TPSR系统架构

4. 系统实现

为了验证面向天地一体化网络的SDN路由架构的可行性和有效性，本文基于Mininet网络仿真平台和Ryu控制器，进行了系统实现和实验验证。下面将具体介绍系统实现的过程：

当数据流从地面网络转发到空间网络后，接入卫星对数据流是否存在业务传输需求进行识别，普通数据根据初始流表直接转发，若存在业务传输需求，接入卫星将数据包转发给控制器，并触发控制器Packet_In动作，控制器对该报文的五元组信息进行解析，得到接入卫星节点S、出口卫星节点D的IP地址信息，计算S到D的n条路径，根据所有路径的剩余带宽、时延大小、丢包率等情况进行评价，当存在最优路径则执行算法1：路径选择算法，否则执行算法2：路径搜索算法。

网络拓扑构建：为了模拟天地一体化网络的拓扑结构，本文在Mininet中搭建了一个由多个交换机和主机组成的虚拟网络拓扑，并将其映射到SDN控制器中进行管理和控制。

路由计算和转发控制：利用Ryu控制器中的路由计算算法和OpenFlow协议以及SR技术，实现对数据包的路由计算和转发控制。路由计算方法TPSR包括路径选择算法和路径搜索算法。

4.1. 路径选择算法

1) 问题描述

从业务需求出发，本文考虑一个网络路径选择优化问题，其中有n个节点和m条边，路径状态由每条边的剩余带宽、时延、丢包率等指标组成，假设每个节点都需要向其他节点发送一定量的数据，路径选择算法的目标是在使用随机K最短路径算法得到的路径集中选择一条最优路径，使得路径的剩余带宽最大，同时满足时延和丢包率的限制。

2) 建立模型

首先，将问题表示成一个线性规划问题。设 $x_{i,j}$ 表示从节点i到节点j的流量大小， $b_{i,j}$ 表示从节点i到节点j的带宽大小， $d_{i,j}$ 表示从节点i到节点j的时延， $l_{i,j}$ 表示从节点i到节点j的丢包率。则上述问题可以定义为目标函数，根据约束条件和变量使用线性规划算法求解评估最优链路问题。可以列出线性规划的模型如下：

$\underset{\left\{x_{i,j}\right\}}{\text{max}}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n}{\sum }}{b}_{i,j}{x}_{i,j}}}$ (1)

约束条件为：

${\displaystyle \underset{j=1}{\overset{n}{\sum }}{x}_{i,j}}-{\displaystyle \underset{j=1}{\overset{n}{\sum }}{x}_{j,i}}=\{\begin{array}{ll}{f}_i\hfill & \text{if}i=s\hfill \\ -f_i\hfill & \text{if}i=t\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$ (2)

$\text{}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_{i,j}}-{\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_{j,i}}=0$ (3)

$l_{i,j}{x}_{i,j}+l_{j,i}{x}_{j,i}\le Loss$ (4)

$d_{i,j}{x}_{i,j}+d_{j,i}{x}_{j,i}\le Delay$ (5)

$x_{i,j}\ge 0$ (6)

$x_{i,j}\le c_{i,j}$ (7)

其中，公式(1)目标函数是总体带宽的和，约束条件包括公式(3)流量守恒约束、公式(6)流量非负性约束、带宽限制约束体现在目标函数公式(1)中、公式(4)丢包率限制约束和公式(5)时延限制约束。其中公式(2)中f_i表示节点i的数据发送量，Loss和Delay分别表示丢包率和时延的限制，公式(7)中c_i,j表示边(i, j)的容量，即该边允许通过的最大流量。

3) 问题求解

为了求解上述线性规划问题，本文使用Scipy.optimize库的linprog函数进行问题求解，相较于其他求解函数，linprog函数采用的是simplex单纯形法和interior-point内点法等高效的求解方法，可以快速地求解较大规模的线性规划问题。在计算精度方面linprog函数采用的是浮点数计算，在数值计算上的精度较高，可以避免因数值误差带来的求解误差。此外，linprog函数提供了许多参数选项，可以控制求解过程中的一些细节，比如求解方法、容忍度等。这些选项可以在求解过程中提高求解效率和求解精度。因此，linprog函数可有效求解线性规划问题。

本文使用linprog函数中的method参数来指定求解方法，求解方法为interior-point方法。求解过程中，首先将问题转换为标准形式，即将不等式约束转换为等式约束。为了实现这一点，本文将不等式约束转化为矩阵乘积的形式，首先定义变量s，将不等式约束 $A_{ineq}x\le b_{ineq}$ 转换为等式约束 $A_{eq}x+s=b_{eq}$ ，其中s的每个元素均为非负数，这可以通过增加一个单位矩阵I的矩阵乘积得到： $A_{ineq}x+s=b_{ineq}$ 等价于 $A_{ineq}x+Is=b_{ineq}$ 。

接下来，将所有约束条件合并为一个大的矩阵形式： $Ax=b$ ，其中 $A=\left[A_{eq}{A}_{ineq}I\right]$ ， $x=\left[\begin{array}{c}xs\end{array}\right]$ ， $b=\left[b_{eq}{b}_{ineq}\right]$ 。

使用linprog函数来解决标准形式的问题，得到一组最优解 $x^{\ast }$ 。但是它并不直接包含所需要的最优路径和带宽信息。将最优解 $x^{\ast }$ 进行解码，得到一组最优的路径和对应的带宽大小。具体来说，将 $x^{\ast }$ 中的变量分成两个部分，即 $x$ 和 $s$ ，将 $x$ 解码为一组路径和带宽大小，将 $s$ 解码为对应的时延和丢包率。最后，验证得到的解是否满足所有约束条件。如果满足，可将其作为最终的解决方案。至此，评估最优链路的问题可通过定义目标函数，约束条件和变量，使用线性规划算法求解完成。

路径选择算法形式化表达如下：

当路径集不存在时，使用路径搜索算法计算一条最优路径。

否则，根据链路剩余带宽bandwidth、丢包率Loss、时延Delay等参数，计算路径综合权重。

最后，遍历路径集中所有路径，选择综合权重最优的路径为最优路径。

4.2. 路径搜索算法

Dijkstra算法是非负权值有向图中搜索单源最短路径的经典算法。本文采用使用ZWK线段树优化后的Dijkstra算法(ZWKD)，相比较于普通线段树为优化手段的Dijkstra算法，ZWKD同样记录每一个点在线段树中叶子节点的编号，但在修改时尽量省去递归来减小常数，进一步降低复杂度。算法主要思路为：在有向网络G中，使用线段树来维护一个存储距离(dis)信息的线段树。每次线段树中的根节点元素即当前节点到对应节点的最短距离，从ZWK线段树中删除，然后进行Dijkstra松弛操作：倘若该节点到左右叶子节点的距离小于S到左右叶子节点的距离，更新dis和线段树节点。

ZWKD算法步骤如下：

1) 初始化：建立一颗ZWK线段树，节点S的dis为0，其他节点的dis为 $\infty$ 。

2) 并将所有的未确定最短路的点放入线段树中。

3) 选择线段树的节点作为距离源点最近的点，并将其从线段树中删除。

4) 对于当前点的每个邻居，如果该邻居已被遍历，则跳过。通过当前点计算从源点到该邻居的更新距离，如果更新后的距离比原来的距离更短，更新该邻居的距离，并在线段树中进行更新。

5) 重复步骤3和4，直到所有的点都已确定。最终结果是一个从源点到其他所有点的距离数组。最后使用目的节点的前驱节点不断回溯，直到回到源节点，路径即为源节点到该节点的前驱节点的序列，且此路径是一条综合负载最轻且不会有链路拥塞的路径，ZWKD算法在比较大的图中可以提高效率，因为线段树可以加速找到距离源点最近的点的过程。ZWKD算法的时间复杂度为O(nlog(n))，与堆优化的Dijkstra算法相比，具有较高的常数。但是，线段树在更新操作时的常数较小，对于空间网络拓扑图中某些链路较为稠密的情况具有更好的效率。ZWKD路径搜索算法在Dijkstra算法的松弛操作中完成，该算法可以在较短的时间内计算最佳的转发路径。

最后，SDN控制器依据最优路径生成流表项，向数据平面下发相应的路由规则，并使用SR技术在数据层面实现数据包的快速转发。

5. 实验验证

5.1. 系统设置

为了获得客观评价，验证面向天地一体化网络的SDN路由架构的可行性和有效性，本文在搭建的虚拟网络拓扑上进行了多组实验。

考虑到本实验对于网络链路状态、设备端到端参数等方面存在一定需求，Mininet与Ryu可高效构建和操作复杂的空间拓扑结构，在本实验中可用来自定义生成虚拟网络拓扑，测试算法效果。因此采用Ryu + Mininet系统组件作为实验环境的基础。在Ubuntu 16.04环境中进行仿真。仿真实验设备的基本硬件配置为Intel (R) Core 10700F CPU@2.9 GHz、16G RAM。实验流程图如图3所示。

Figure 3. Experimental flowchart

图3. 实验流程图

首先，仿真系统根据卫星网络规模使用Mininet生成自定义卫星网络拓扑。然后，初始化网络生成一维最短路径，随机选择其中两点作为接入卫星和出口卫星，使用路由计算方法获得最优路径。并使用ping命令生成icmp数据流，Iperf发送不同类型的数据流，多次变化输入，并重复实验，最后取平均值作为实验数据结果。

图4显示了在自定义拓扑中，向交换机发送的需要安装的流表项信息，栈内标签信息为{262144, 524293, 524292}，最后压栈的栈顶标签为{524292}，将其发送到交换机eth2端口绑定的组表。

Figure 4. Switch push stack flow table entry

图4. 交换机压栈流表项信息

图5显示了在自定义拓扑中应用分段路由技术后，交换机的流表项，包括初始化流表项、MAC信息表项以及转发表项，转发表项所包含的信息为重路由设置的动作集。

Figure 5. Forwarding table entries built with SR switch

图5. 采用分段路由交换机构建的转发表项

图6显示了使用wireshark抓包工具抓到的标签信息组成的段列表的ICMP数据包信息。从数据包信息可以看到，从标签信息依次为524292、524293，262144，IP地址10.0.11.1的接入卫星发送至IP地址10.0.11.2的出口卫星。

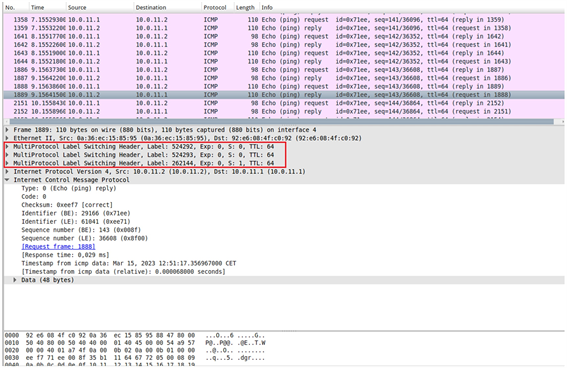
Figure 6. Wireshark capture packet label information

图6. Wireshark抓包标签信息

综上所述，为了验证系统的可行性和有效性，本文通过Mininet网络仿真平台和Ryu控制器，实现了面向天地一体化网络的SDN路由基础系统架构，并在搭建的虚拟网络拓扑上进行了多组实验。实验结果表明，该架构可以实现对网络的高效控制，同时具有较高的可靠性。

5.2. 算法优化效果

为了验证所提TPSR算法的优化效果，仿真系统使用Mininet搭建虚拟网络拓扑Fat-Tree (k = 4)模拟空间网络局部拓扑结构，其中地面站连接网络拓扑的边缘节点。如图7所示。

Figure 7. Partial space network topology Fat-Tree (k = 4)

图7. 局部空间网络拓扑Fat-Tree (k = 4)

为了验证TPSR采用SDN结合SR部署方案对空间网络流表项开销的优化情况，通过对TPSR在数据层面是否采用SR技术对比流表数目。由图8，若在数据层面直接下发流表项，整个网络拓扑的流表开销可达近300条。若在数据层面使用采用SR技术，TPSR仅需在最优路径中的少数网络设备推送流表项(用于将最优路径节点标签生成的SL压入路径头节点)，因此，单个数据流所需流量条目很小。一般数据包转发时只仅需匹配默认流表项，与不采用SR的N-TPSR相比，TPSR显著降低了流表项开销，TPS最多可减少46%的流表项开销。采用TPSR方案，在减少流表项开销的同时，也确保了空间网络的传输性能。

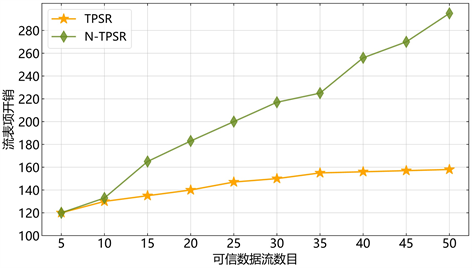
Figure 8. Flow table overhead comparison

图8. 流表开销对比

为了验证TPSR计算得到的路径的传输性能，在不同的链路负载条件下从时延、链路转发速率，丢包率等三个指标出发，对比TPSR与经典Dijkstra、等价多路由算法(ECMP)以及N-TPSR实际性能。图9为四种算法对于时延指标的对比结果，在实验中，当链路负载低于40%时，由于负载较低，四种算法的时延均为处于较低水平。当链路负载处于40%~80%之间时，TPSR和N-TPSR时延要低于Dijkstra、ECMP算法。这是由于Dijkstra和ECMP算法无法通过链路的即时状态进行路径调整，而TPSR在计算路径时更均衡的考虑各条链路端到端时延数据，在业务流在路径传输时，链路发生局部拥塞的情况大大改善。当链路负载情况大于80%后，出现网络拥塞的几率则会大大提升，所以四种算法的优化效果差异不明显。

Figure 9. Average delay comparison

图9. 平均时延对比

图10为四种算法对于链路转发速率(吞吐量)指标的对比结果，在实验中，随着链路负载逐渐提升，四种算法所对应的链路转发速率保持上升趋势。当链路负载在80%左右时，由于星间链路ISL带宽以及算法性能限制，链路转发速率处于稳定，最终达到链路传输能力的瓶颈。其中，当链路负载提升至40%以后，TPSR和N-TPSR要明显优于Dijkstra、ECMP算法，带宽利用率提升20%左右。这是TPSR基于各条链路最大剩余带宽数据计算出最优路径，链路剩余带宽资源能够得到更充分的利用。

Figure 10. Average forwarding rate comparison

图10. 平均转发速率对比

图11为四种算法对于链路丢包率指标的对比结果，在实验中，由于链路负载在40%左右时，链路状况较好，四种算法的丢包率均为0，当链路负载大于40%后，链路中开始发生丢包。而后，随着链路负载率逐渐上升，链路丢包率也同样保持上升趋势。其中，当链路负载提升至40%以后，TPSR和N-TPSR相较于其他两种对比算法具有一定优势。当链路负载在80%左右时，四种方法的丢包率均趋于稳定。

Figure 11. Average packet loss ratio comparison

图11. 平均丢包率对比

6. 结语

本文主要对面向天地一体化网络的SDN路由架构进行了研究和探讨。介绍了SDN技术和面向天地一体化网络的背景和意义。面向天地一体化网络，引入了一种SDN结合SR路由架构。阐述了面向天地一体化网络的SDN路由系统的具体实现方法和关键技术。并详细介绍了TPSR路由方案，包括路径选择算法和基于ZWK线段树改进后路径搜索算法的具体思路，以及系统其他主要模块的工作原理。最后，在实验验证中，本文进行了多组实验来验证架构的可行性和有效性。综合以上分析和实验结果，可得出以下结论：面向天地一体化网络的SDN路由架构能够有效地提高网络的可靠性、稳定性、传输性能。在面向天地一体化网络的应用中具有广泛的前景和应用价值。