基于FNN的直驱式波浪发电系统PID控制

PID Control of Direct Drive Wave Power Generation System Based on FNN

摘要: 本文在分析浮子水动力模型和永磁同步线性发电机模型的基础上，得到了最大功率捕获条件。然后，将改进的模糊神经网络PID (RFNNP)控制算法应用于最大功率点跟踪控制。通过对模糊神经网络结构的分析，在模糊神经网络中加入Relu激活函数，构建了RFNNP控制。将模糊规则与神经网络的自学习能力相结合，根据海况变化调整PID参数，使RFNNP算法更准确地逼近非线性目标模型。仿真结果表明，采用该策略的波能转换系统是有效可行的。

Abstract: Based on the analysis of float hydrodynamic model and permanent magnet synchronous linear generator model, the maximum power capture conditions are obtained. Then, the improved fuzzy neural network PID (RFNNP) control algorithm is applied to the maximum power point tracking control. By analyzing the structure of fuzzy neural network, adding Relu activation function into the fuzzy neural network, RFNNP control is constructed. The fuzzy rules are combined with the self-learning ability of neural network, and PID parameters are adjusted according to the change of sea state, so that RFNNP algorithm approximates the nonlinear target model more accurately. The simulation results show that the wave energy conversion system using this strategy is effective and feasible.

1. 引言

波浪能作为一种清洁的可再生资源，具有功率密度高，蕴藏能量巨大、无污染、可预测等特点，是扩充海洋资源丰富国家的能源重要途径 [1] [2] 。因此，波浪能备受人们广泛关注。捕获最大功率下的波浪能对未来能源资源的可持续利用具有战略意义 [3] 。然而，大多数波浪能转换系统都包含变速箱等复杂的传动机构，导致能量转换效率 [4] 较低。直接驱动波浪发电系统通过永磁同步线性发电机(PMSLG)将浮子的运动直接转化为电能，节省了中间传动机构 [5] [6] [7] 的能量损失。因此，研究适合直接驱动波浪能变换器(WEC)系统的功率优化控制策略，对于进一步提高海洋捕获功率 [8] 具有重要意义。

目前，文献 [9] [10] [11] [12] 中的波浪发电系统广泛采用传统PID控制。但由于海浪的振幅和频率变化频繁，传统PID控制参数是固定的，无法实时调整，因此在海洋条件变化的情况下，相对难以准确跟踪目标值。在直驱波系统中采用模糊PI控制器跟踪最优参考值，文献 [13] 中采用模糊规则自适应调节PI控制增益参数。文献 [14] 采用模糊神经网络PID (FNNP)控制，利用神经网络的学习能力不断减小误差值，实现PID参数的自适应调节。同时，波浪发电系统还采用了其他一些方法来达到的最优功率值 [15] [16] 。文献 [17] 中，采用电流斩波电路控制开关磁阻电机的动作，使浮子与波浪同步运动，从而获得最大功率。文献 [18] 提出了一种经济模型预测控制方法。它不仅可以扩大海况下的安全作业范围，还可以提高能源生产效率。

综上所述，本文采用基于智能控制的PID控制。通过对浮子水动力模型和PMSLG模型的分析，得到了捕获最大功率的条件。本文将一种改进的模糊神经网络PID (RFNNP)控制应用于提取功率最大化的最优控制。通过在模糊神经网络(FNN)中加入Relu激活函数，形成RFNNP，使控制能够最大限度地逼近非线性目标模型。同时，利用模糊神经网络内部参数的迭代更新，不断减小目标误差。最后，通过仿真验证了基于RFNNP控制的WEC的正确性和可行性。

2. 波浪发电系统建模与分析

2.1. 水动能模型

波浪发电系统整体结构如图1所示。浮子和直线电机通过连接器件形成刚性连接，统称为运动部件。浮子受到波浪激励作用后上下运动，带动电机动子切割磁场，吸收海洋表面波浪能，通过电机旁侧的转换器(MSC)转换为电能。在本文中，仅考虑浮子的上升和下沉两个方向。因此，浮子摆动的水动力方程可以表示为公式所示：

$m\ddot{z}=F_e+F_r+F_v+F_b+F_g$ (1)

在公式(1)中，m代表运动部件的总质量， $\ddot{z}$ 代表浮子的运动方向的加速度， $F_e$ 为波浪作用在浮子上的激发力， $F_r$ 代表的是辐射力， $F_v$ 是粘滞力， $F_b$ 代表的是浮子的浮力， $F_g$ 为永磁同步线性发电机产生的电磁力。

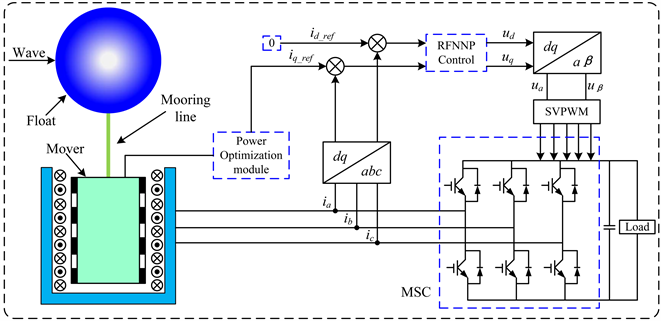
Figure 1. Structure diagram of wave power generation system

图1. 波浪发电系统结构图

在规则波作用的情况下，辐射力 $F_r$ 通常可以描述为公式(2)所示：

$F_r=-m_a\ddot{z}-c_r\stackrel{\dot{}}{z}$ (2)

在公式(2)中， $m_a$ 是附加质量， $c_r$ 代表水动力阻尼系数。电磁力 $F_g$ 可以表示为公式(3)所示：

$F_g=-R_g\stackrel{\dot{}}{z}$ (3)

在公式(3)中， $R_g$ 代表永磁同步线性发电机有源分量的阻尼系数。浮子的浮力 $F_b$ 能表示为公式(4)所示：

$F_b=-\rho gAz=-k_b\stackrel{\dot{}}{z}$ (4)

在公式(4)中，A代表水面处浮子的面积大小， $\rho$ 代表海水的密度， $k_b$ 是水动力刚度系数。粘滞力 $F_v$ 可以表示为公式(5)所示：

$F_v=-c_v\stackrel{\dot{}}{z}$ (5)

在公式(5)中， $c_v$ 代表粘滞力的阻尼系数。因此，通过公式(2)，(3)，(4)和公式(5)可得，将上述公式带进公式(1)中，易得波浪作用在浮子上的激励力 $F_e$ ，表示为公式(6)所示：

$F_e=\left(m+m_a\right)\ddot{z}+\left(c_r+R_g+c_v\right)\stackrel{\dot{}}{z}+k_{b}z$ (6)

2.2. PMSLG数学模型与分析

在波浪发电系统中，永磁同步线性发电机负责将浮子捕获的海洋波浪能转换为电能，并在定子绕组中产生三相电流。以永磁同步线性发电机的d-q轴作为参考系，可知永磁同步线性发电机的模型为公式(7)所示：

$\begin{array}{l}{u}_d=-R{i}_d+w{L}_q{i}_q-L_d\frac{\text{d}{i}_d}{\text{d}t}\\ u_q=-R{i}_q+w{L}_d{i}_d-L_q\frac{\text{d}{i}_q}{\text{d}t}+w{\psi }_L\end{array}$ (7)

在公式(7)中， $u_d$ 和 $u_q$ 代表着定子d-q轴两端电压， $i_d$ 和 $i_q$ 代表定子d-q轴两端电流， $L_d$ 和 $L_q$ 代表定子绕组的d-q轴的电感，R代表定子的电阻， ${\psi }_L$ 代表永磁体的磁链，w代表定子的旋转的角速度。

根据上述可得，永磁同步线性发电机产生的电磁力表示为公式(8)所示：

$F_e=\frac{3\pi }{2\tau }\left[{\psi }_L{i}_q-\left(L_q-L_d\right)i_d{i}_q\right]$ (8)

假设永磁同步线性发电机中的气隙均匀，则有 $L_q=L_d$ ，则公式(8)则等价于公式(9)所示：

$F_e=\frac{3\pi }{2\tau }{\psi }_L{i}_q$ (9)

此外，忽略永磁同步线性发电机内部能量损耗，可以得出永磁同步线性发电机从海洋波浪中提取的平均能量为公式(10)所示：

$P_a=\frac{{\displaystyle {\int }_0^T{F}_g\stackrel{\dot{}}{z}\text{d}t}}{T}$ (10)

2.3. 规则波最大功率捕获

在海洋平面的规则波作用下，公式(6)的二阶微分方程可以表示RLC等效电路，等效电路图如图2所示。其中 $F_e$ 代表等效电路中的电源， $z_v$ 代表电路中的电流， $F_g$ 代表对应电阻上的电压。

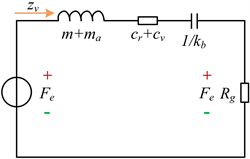
Figure 2. Hydrodynamic equivalent circuit of float

图2. 浮子水动力等效电路

结合图2以及公式(6)，系统提取的平均功率 $P_g$ 可以表示为公式(11)所示：

$P_g=F_g{z}_v=\frac{{\left|F_e\right|}^2}{4\left(c_r+c_v\right)}\left(1-{\left|\left(\frac{\left(c_r-R_g+c_v\right)-j\left[w\left(m+m_a\right)-\frac{k_b}{w}\right]}{\left(c_r+R_g+c_v\right)+j\left[w\left(m+m_a\right)-\frac{k_b}{w}\right]}\right)\right|}^2\right)$ (11)

在实际理论中，为了实现提取的功率最大化，上述公式应同时满足公式(12)所示的条件。

$\{\begin{array}{l}{R}_g=c_r+c_v\\ k_b=w^2\left(m+m_a\right)\end{array}$ (12)

2.4. 不规则波最大功率捕获

实际的海浪信号可以看作是不同的频率分量的正弦信号或者余弦信号的线性叠加而成，对于海洋中的一些随机扰动，它们大多具有较短的周期和较低的振幅。因此可利用傅里叶变换将海浪分解为如下形式：

$F_e=F_{e1}+F_{e2}+\cdot \cdot \cdot +F_{en}$ (13)

$F_{en}=A_n\sin \left(w_n+{\Phi }_n\right)$ (14)

在公式(13)和公式(14)中， $n=1,2,3,\cdot \cdot \cdot$ ， $A_n$ ， $w_n$ 和 ${\Phi }_n$ 分别代表着 $F_{en}$ 的幅值，频率以及相位。

在不通的海浪激励作用下，运动部件或产生不同的水动力反馈。因此，公式(6)可以表示成如下形式：

$\{\begin{array}{l}\left(m+m_{a1}\right){\ddot{z}}_1+\left(c_{r1}+R_{g1}+c_v\right){\stackrel{\dot{}}{z}}_1+k_b{z}_1=F_{e1}\\ \cdots \\ \left(m+m_{an}\right){\ddot{z}}_1+\left(c_{rn}+R_{gn}+c_v\right){\stackrel{\dot{}}{z}}_n+k_b{z}_n=F_{en}\end{array}$ (15)

在公式(15)中， $m_{an}$ ， $c_{rn}$ 和 $R_{gn}$ 代表各 $F_{en}$ 下对应的水动力参数。因此，系统总功率 $P_a$ 可以描述为公式(16)所示：

$P_a={\displaystyle \underset{k=1}{\overset{n}{\sum }}{F}_{gk}{\stackrel{\dot{}}{z}}_k={\displaystyle \underset{k=1}{\overset{n}{\sum }}{P}_k}}$ (16)

在公式(16)中， $F_{gk}$ ， ${\stackrel{\dot{}}{z}}_k$ 和 $P_k$ 分别代表各 $F_{en}$ 对应的电磁力，速度和功率。因此，当求得每个 $F_{en}$ 下的最优值时，总功率值能够取得最大。

3. 改进FNN的建模与分析

3.1. FNN网络结构

模糊神经网络(Fuzzy Neural Network, FNN)本质上是一种将模糊理论与人工前向神经网络相结合的多层前向神经网络。FNN将模糊控制规则的知识应用到神经网络中，对输入信号进行逐层计算和处理，输出PID控制所需的三个参数，最后将其输入PID控制器进行在线调节。FNN的结构如图3所示。

Figure 3. FNN structure diagram

图3. FNN结构图

如图3所示，第一层是输入层， $I_L$ 和 $O_L\left(L=1,2,3,4\right)$ 分别表示每一层的输入和输出数据。假设 $x_1=e$ ， $x_2=e_c$ ，则第一层的网络输入和输出如公式17所示：

$\{\begin{array}{l}{I}_i=x_i\\ O_i=I_i\end{array}$ (17)

第二层是模糊化层，它可以将输入信号划分为7个模糊子集，最后的输出属于函数值。 $c_{ij}$ 和 $b_{ij}\left(i=1,2;j=1,\cdots ,7\right)$ 分别为高斯函数的中心值和宽度。第一层的输入和输出如公式(18)所示：

$\{\begin{array}{l}{I}_2=O_1\\ O_2=G_{ij}=\exp \left(-\frac{{\left(x_i-c_{ij}\right)}^2}{b_{ij}{}^2}\right)\end{array}$ (18)

第三层是模糊推理层。神经元的数量等于模糊规则的数量。这一层的目标是输出每个模糊规则的适应度。第三层的输入和输出如公式(19)所示，其中k代表第二层的神经元， $i_1,j_1=1,\cdots ,7$ 。

$\{\begin{array}{l}{I}_3=O_2\\ O_3=f_{3(k)}=G_{1i_1}*G_{2j_1}\end{array}$ (19)

最后一层是解模糊层，目的是计算PID的三个控制参数。第三层的输入和输出如公式(20)所示：

$\{\begin{array}{l}{I}_4=f_{4(l)}={\displaystyle \underset{k=1}{\overset{N}{\sum }}{f}_{3(k)}*w_{lk}}\\ O_4=g\left(I_4\right)\end{array}$ (20)

在公式(20)中，N = 49， $w_{lk}$ 代表连接第三层和最后一层的权重系数， $l=1,2,3$ ， $g()$ 代表激活函数。

3.2. 激活函数

本文采用Relu激活函数应用在图3所示的FNN结构图中的第四层，形成改进的模糊神经网络(RFNN)，通过改进后的网络能够更准确的拟合目标模型。Relu激活函数示意图如图4所示。

Figure 4. Relu activation function

图4. Relu激活函数

综上所述，通过本文对FNN结构的分析，解决上述缺陷，采用Relu激活函数g(x)。它的表达式如公式21所示：

$g\left(x\right)=\{\begin{array}{l}0x\le 0\\ xx>0\end{array}$ (21)

由公式(21)可知，激活函数g(x)的梯度在x轴的正半轴上并没有消失，可以通过神经网络学习到梯度值。Relu激活函数能够输出一个真正的零值，能够使得负输入可以输出真零值，允许神经网络中的隐藏层激活包含一个或多个真零值。这种表示称做稀疏表示，这种性质能够加速学习和简化模型。此外，g(x)的推导也非常简单，大大缩短了收敛时间，更准确地接近目标值。

3.3. RFNN梯度下降法

根据图3可知，模糊神经网络结构最后一层输出三个参数，分别是 $K_p$ ， $K_i$ ， $K_d$ 。模糊神经网络在输出三个参数后将其送入PID控制器。PID算法的离散形式如公式(22)所示：

$u\left(k\right)=K_{p}e\left(k\right)+K_i{\displaystyle \underset{i=0}{\overset{k}{\sum }}e\left(i\right)+K_d\left[e\left(k\right)-e\left(k-1\right)\right]}$ (22)

在公式(22)中， $K_p$ ， $K_i$ ， $K_d$ 的系数分别等于 $x_l=\left(l=1,2,3\right)$ ，RFFNP详细控制流程图如图5所示。在图5中，PID控制器接收到RFNN传递的三个参数，并生成 $u_{(k)}$ 传递给永磁同步直线电机。永磁同步直线电机产生的电流i作为残差连接反馈给RFNN之前的信号，以此达到实时调整PID控制器的三个参数。

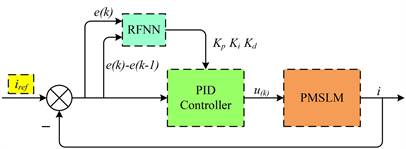
Figure 5. Schematic diagram of RFNNP control

图5. RFNNP控制示意图

在RFNNP过程中，定义成本函数为公式(23)所示：

$E=\frac{1}{2}{e}^2=\frac{1}{2}{\left(r_i-y_o\right)}^2$ (23)

在公式(23)中， $r_i$ 代表参考输入电流值， $y_o$ 代表实际输出电流值。因此， $w_{ij}$ ，a， $c_{ij}$ ， $b_{ij}$ 的变化如下公式所示：

$\begin{array}{l}-\frac{\partial E}{\partial w_{lk}}=-\eta \frac{\partial E}{\partial e}\frac{\partial e}{\partial y_o}\frac{\partial y_o}{\partial u}\frac{\partial u}{\partial O_4}\frac{\partial O_4}{\partial I_4}\frac{\partial I_4}{\partial w_{lk}}\\ =\eta e\frac{\partial y_o}{\partial u}{x}_l\left(2I_4+a\right)f_{3(k)}=S{f}_{3(k)}\end{array}$ (24)

$-\frac{\partial E}{\partial a}=\eta e\frac{\partial y_o}{\partial u}{x}_l{I}_4$ (25)

$-\frac{\partial E}{\partial b_{ij}}=S\underset{m=1}{\overset{N}{{\displaystyle \sum }}}\left(w_{lk(m)}{O}_{3(m)}\frac{-2{\left(x_i-c_{ij}\right)}^2}{b_{ij}^3}\right)$ (26)

$-\frac{\partial E}{\partial c_{ij}}=S\underset{m=1}{\overset{N}{{\displaystyle \sum }}}\left(w_{lk(m)}{O}_{3(m)}\frac{-2\left(x_i-c_{ij}\right)}{b_{ij}^2}\right)$ (27)

在上述公式中， $\eta$ 代表神经网络的学习率，N代表着目标函数E到目标参数的路径数。目标参数的迭代更新公式如下公式所示：

${w_{lk}|}_n={w_{lk}|}_{n-1}-\frac{\partial E}{\partial w_{lk}}+a\left({w_{lk}|}_{n-1}-{w_{lk}|}_{n-2}\right)$ (28)

${a|}_n={a|}_{n-1}-\frac{\partial E}{\partial a}+a\left({a|}_{n-1}-{a|}_{n-2}\right)$ (29)

${b_{ij}|}_n={b_{ij}|}_{n-1}-\frac{\partial E}{\partial b_{ij}}+a\left({b_{ij}|}_{n-1}-{b_{ij}|}_{n-2}\right)$ (30)

${c_{ij}|}_n={c_{ij}|}_{n-1}-\frac{\partial E}{\partial c_{ij}}+a\left({c_{ij}|}_{n-1}-{c_{ij}|}_{n-2}\right)$ (31)

在上述公式中，a代表神经网络的动量因子，n代表迭代次数。

4. 仿真与分析

本文基于Simulink平台建立直接驱动波浪发电系统的模型，并通过仿真验证模型与所提策略的正确性。根据浮子的水动力模型，表1给出了T = 2 s时模拟所用的水动力参数。表1中海水密度、重力加速度、水动力阻尼系数、粘滞系数、刚度系数各项数值均为物理标准测量值，激励力为海浪作用在浮子上实测数值，附加质量为发电系统其他附加部件实际质量。

Table 1. Parameters of wave power generation system

表1. 波浪发电系统参数

规则波下的模拟结果如图6，图7，图8以及图9所示。在保持其他参数一致的情况下，图6，图7以及图8分别为PID算法、FNNP算法和RFNNP算法对最大功率点的跟踪控制结果。为了更好地验证模型的可行性，不难看出，海浪的初始环境为激振力设为9810 N，T = 4 s。当t = 16 s时，激振力周期保持不变，振幅变为8000 N。t = 28 s时，激振力的幅值变为6700 N，T = 2 s。

由图6，图7以及图8中可以看出，当永磁线性同步发电机速度最大时，跟踪误差相对最大。在PID算法控制的q轴电流跟踪曲线中，最大跟踪误差可达2 A，误差范围为PID算法跟踪误差的3/5左右。但可以看出，RFNNP算法控制的q轴电流相对平滑，具有最好的精度。误差范围约为−0.5 A~0.5 A，误差值约为FNNP算法的5/9。总体而言，RFNNP算法可以更好地跟踪参考电流值，实现对最大功率点的准确跟踪。

Figure 6. PID control q axis current

图6. PID控制q轴电流

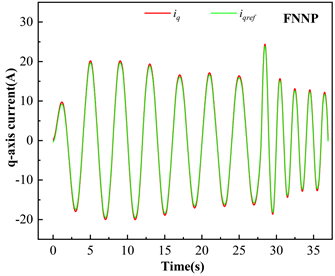
Figure 7. FNNP control of q axis current

图7. FNNP控制q轴电流

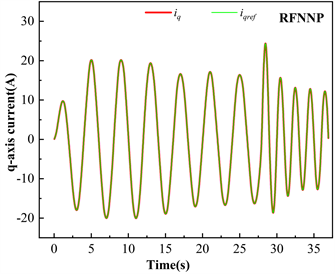
Figure 8. IFNNP controlled q axis current

图8. IFNNP控制q轴电流

Figure 9. Comparison of average power

图9. 平均功率的比较

从图9中可以看到三种算法下从海洋中提取的平均功率的对比。RFNNP算法控制下提取的平均功率比FNNP算法控制下的平均功率高约50 W，在某些点比PID算法控制下的平均功率高120 W。因此，RFNNP控制具有更高的精度。

为了更好地验证本文提出的RFNNP控制的高鲁棒性，本文对随机波条件下进行仿真验证结果分析。图10为随机海况下的波浪激励力的波形。图10中的波浪激励力波形主要由以下四个频率分量组成：F_e1 = 9810 N，T = 4 s；F_e2 = 6700 N，T = 2 s；F_e3 = 11200 N，T = 8 s；F_e4 = 8200 N，T = 3 s。

当WEC系统的输入为图10中的波浪激励力时，得到系统输出的平均功率，如图11所示。可以看出，总体上RFNNP算法提取的平均功率与其他两种算法相比是最高的。RFNNP算法较之FNNP算法，在神经网络层引入Relu激活函数，因此可以加快收敛速度，提高平均功率；较之PID算法，则是在Relu激活函数之上同时引入FNN，能够加快PID内部参数自更新，提升转换效率。综上所述，RFNNP算法用于WEC系统的最大功率点轨迹控制是有效可行的。此外，在相同的海洋条件下，它可以提高WEC系统从海洋提取的平均功率。

Figure 10. Wave excitation wave form

图10. 波浪激励波形

Figure 11. Comparison of average power

图11. 平均功率的比较

5. 总结

本文利用提出的RFNNP算法构建了一个直驱式的WEC系统来优化取电策略。首先，对浮子和PMSLG的模型进行了分析，得到了最大功率条件。其次，将模糊规则以神经网络的形式表达，在FNN中引入Relu激活函数，利用神经网络的自学习能力更新内部目标参数以减小误差，从而跟踪参考值。实验结果表明，本文所提出的RFNNP算法能够更准确地跟踪最大功率点，跟踪趋势更加平滑。同时，在相同的波浪条件和参数设置下，由RFNNP算法控制的波浪能转换器转换效率更高。基于此，本文研究的RFNNP算法跟踪最优功率点具有一定可行性和有效性。

NOTES

^*通讯作者。