某新能源轿车车架的静态结构与模态分析

Static Structure and Modal Analysis of a New Energy Car Frame

摘要: 车架作为汽车总成重要的组成部件，本文通过Solidworks软件三维建模，设计了一种铝合金材料新能源轿车车架模型，并基于有限元方法，运用Ansys软件在不同工况下的仿真，着重分析了车架的结构强度，扭转刚度及自由模态振型。结果表明，该车架在满载工况时的强度与刚度满足设计要求，并在激励源的作用下无共振现象，同时实现轻量化设计，采用新材料相较于传统汽车钢减重50%。

Abstract: Frame is an important component of automobile assembly. In this paper, a new energy car frame model made of aluminum alloy material is designed by using Solidworks 3D modeling software. Based on finite element method and Ansys software simulation under different working conditions, the structural strength, torsional stiffness and free mode shape of the frame are analyzed emphati-cally. The results show that the strength and stiffness of the frame under full load condition meet the design requirements, and there is no resonance phenomenon under the action of the excitation source. At the same time to achieve lightweight design, the use of new materials compared to the traditional automobile steel weight reduction of 50%.

1. 引言

近年来，随着人们的环保意识也不断提高，新能源汽车行业发展迅速，逐渐取代燃油车占据了一定的市场地位，而伴随着新能源汽车数量的增长，安全性、舒适性的需求也逐渐有目共睹 [1] 。汽车车架作为新能源汽车的关键支承，它作为汽车底盘的核心部件，对汽车整机的性能和结构可靠性有着重要的影响，在行驶过程中受到及其复杂的交变载荷影响，在不同工况下产生结构失效，许多企业在传统结构上加以改造的同时，组建燃料电池、电机以及伺服控制元件，也要考虑轻量化设计，以提高电池效率 [2] [3] 。基于有限元法可以缩短研发周期，弥补传统设计的短板，因此对新能源汽车车架的有限元分析及模型再设计非常有意义。

方朝等人提出一种纯电旅游观光车车架，并通过多次局部迭代拓扑优化的方法对其进行了精细化设计 [4] 。陈和娟以轻量化赛车为研究对象，应用ANSYS软件对车架结构进行了有限元分析，验证了车架的弯曲扭转刚度 [5] 。马嘉俊等人在参考传统边梁式车架的基础上，应用6000系铝合金材料设计了一种直驱式电动汽车副车架，并利用NX10.0软件优化了车架结构，为新能源车架轻量化设计提供了依据 [6] 。但目前，大梁式车架仍为主流车架形势 [7] ，采用合理方法对车架适应性改进，才能充分发挥新能源汽车的性能以及现代化优势。

本文以某型新能源轿车车架为研究对象，使用ANSYS Workbench分别进行相应的状态约束，重点模拟了车架在满载弯曲、满载扭转，平衡工况下新能源汽车主梁的静力学特性分析以及动力学模态分析，并通过相应的计算验证新材料力学性能是否满足强度和刚度的要求。

2. 新能源轿车车架结构分析与有限元模型

2.1. 结构分析

该车架由两根横梁、两根纵梁以及两根辅助梁组成，中间部位设计驾驶室简图以辅助有限元分析，相互之间通过焊接连接在一起。每段梁均采用空心管材，电池储藏盒设计于中部和后部，电池盒与主梁之间采用阻燃PC/ABS材料连接，既能实现轻量化，又能起到阻燃、耐低温的作用 [8] 。

车架具体设计数据为：长3200 mm，宽770 mm，高250 mm，主梁截面长24 mm，宽16 mm电池储藏室长度2000 mm，该新能源车架结构简图如图1所示。

2.2. 三维模型建立

通过Solidworks三维软件对新能源轿车车架进行建模，基于能量最小化原则，结构的简化表示和上负载的实际表示视作等效负载，建模过程中过滤掉影响较小的因素 [9] 。新能源车架三维模型如图2所示。

2.3. 材料及网格划分

车架材料选用铝合金7系7075-T6，该系型材焊接性能较为出色，重量轻，抗氧化能力强，可满足新能源车架的使用要求，材料力学性能如表1所示，车架的重量为113.278 kg，而使用常规结构钢合金的底盘实际重量为210 kg左右 [10] 。

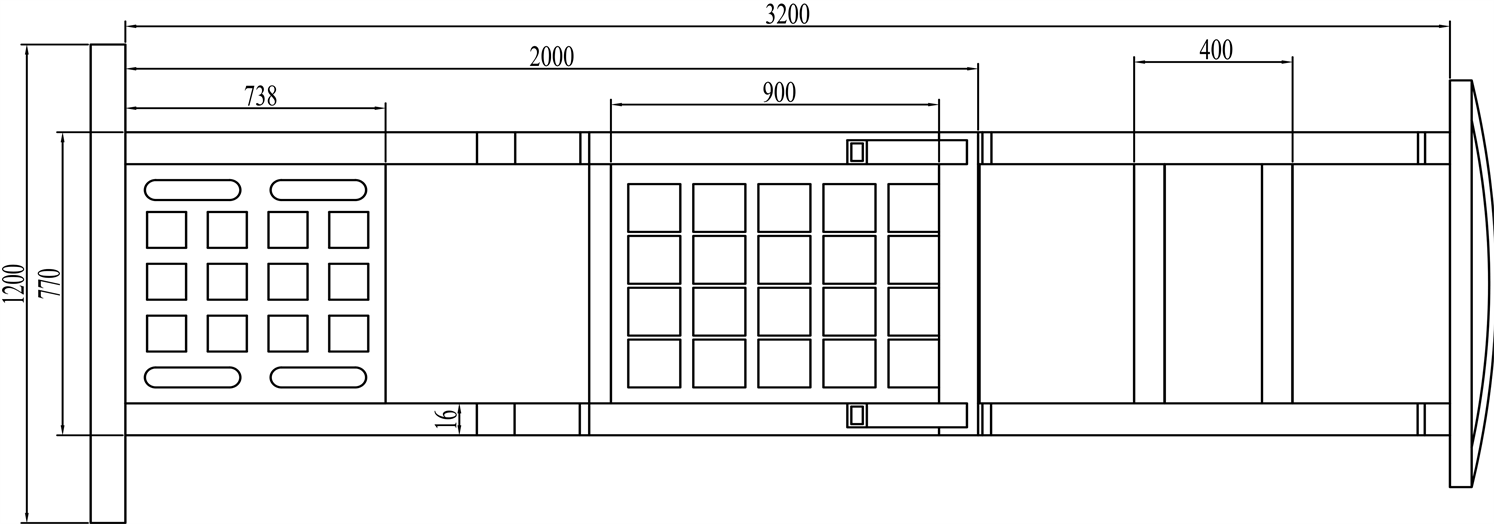
Figure 1. Schematic diagram of new energy frame structure

图1. 新能源车架结构简图

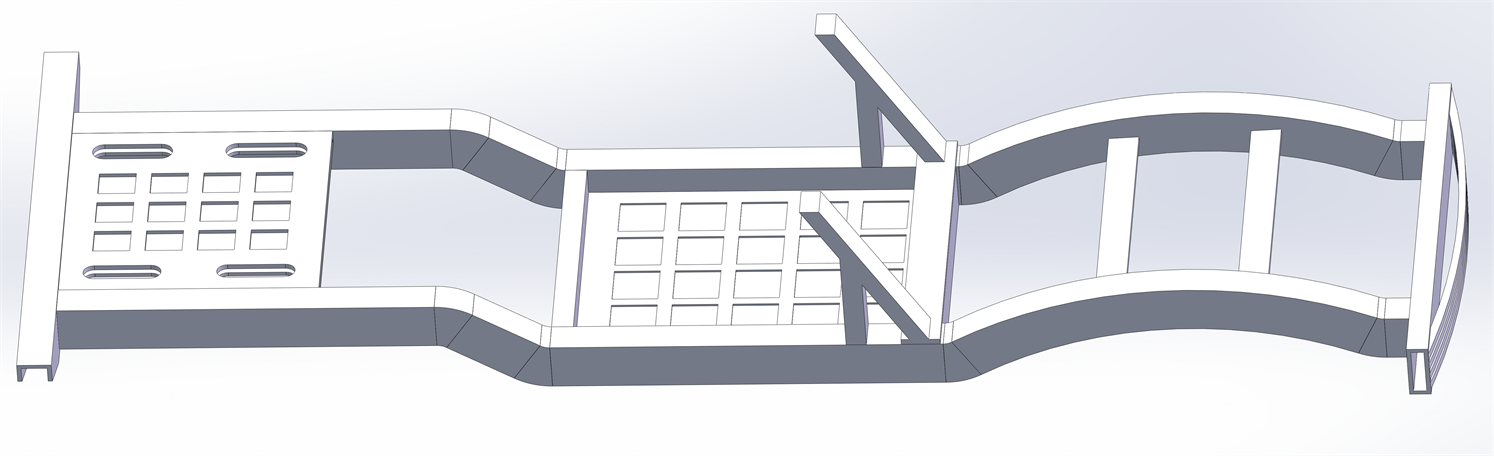
Figure 2. A three-dimensional model of the vehicle frame

图2. 车架三维模型

Table 1. Mechanical property parameters of 7075-T6 aluminum alloy

表1. 7075-T6铝合金的力学性能参数

Figure 3. Schematic diagram of grid partitioning strategy

图3. 网格划分策略示意图

将车架模型导入Ansys Workbench建立分析项目，网格的的疏密程度直接影响CPU的计算时间，为提高计算效率，通过Spaceclaim模块抽取中面，并将一般网格大小设置为5 mm，局部为3 mm，主梁应用四边形单元，局部特殊区域应用三边形单元，两种单元类型组合使用，相应方法如图3所示，对于局部区域，减小单元尺寸是最有效的网格细化策略，其本质是减小整个建模与的单元尺寸，从而提高网格精度，进而确定好焊接模型的接触关系，这里取面与面、面与边识别的容差值为3.9 mm，最终划分了238,420个节点，250,918个单元，划分结果如图4所示。

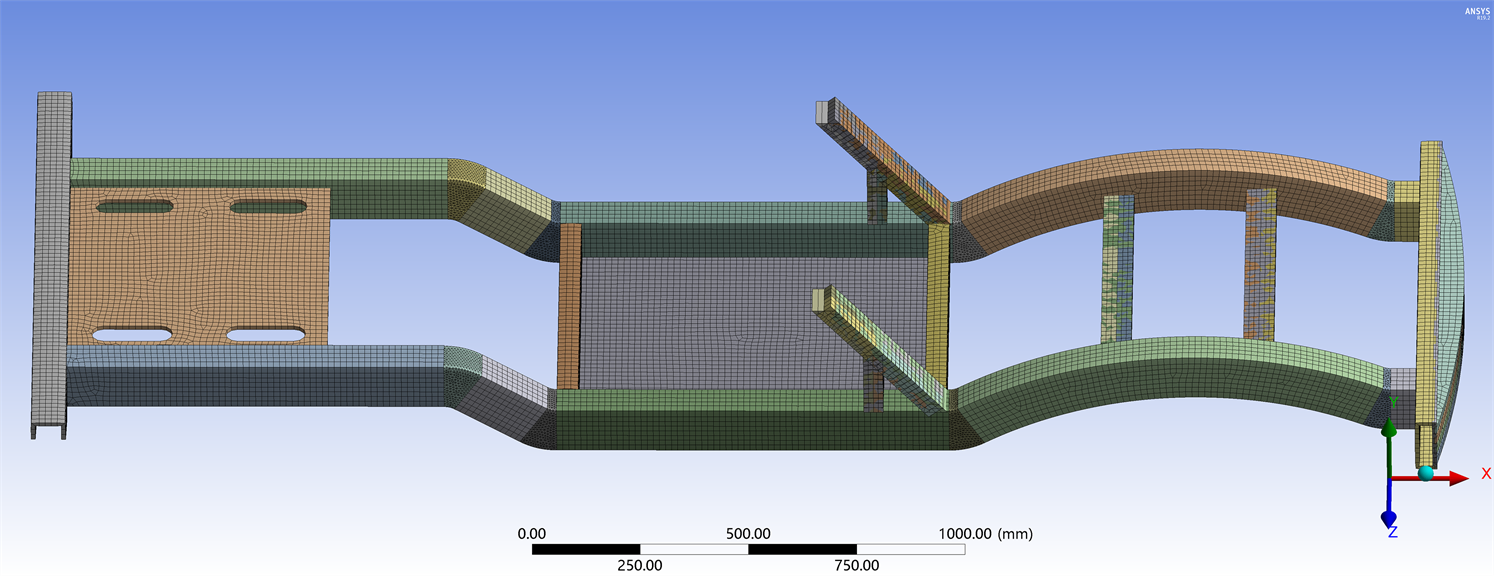
Figure 4. Grid partitioning model for the main beam of the vehicle frame

图4. 车架主梁网格划分模型

2.4. 车架基本载荷的确定

在对车架主梁结构分析过程中，确定实际中涉及的集中载荷，它对应的载荷包括驾驶员及其他成员、动力电池、电机、白车身以及备胎等等，本文研究主要载荷及其对应的分布位置如表2所示。

Table 2. Load table for main beam of vehicle frame

表2. 车架主梁载荷表

为将载荷施加到主梁上，研究过程还需要具体分析，合理有效并且贴合实际。本文在根据理论分析基础上，综合考虑满载时车架的承受方式，确定以均布施加这种载荷方式为主，汽车在行驶过程中又受路面状况、驾驶员习惯等不确定性因素影响，受到复杂的动静载荷联合施加，将上述相关载荷分别相关到一个动载系数上 [11] 。本文取动载系数K_v = 2，载荷分布方式如图5所示。在约束载荷施加过程中遵守以下规则：

1) 约束施加保证模型不存在欠定义，避免模型移动产生较大的计算偏差；

2) 约束中亦不存在模型过定义；

3) 遵守力学平衡规则，如主梁反力与被施加的其他载荷相等；

4) 载荷大小方向定义明确。

3. 新能源车架静力学特性分析

3.1. 不同工况下的结构静强度分析

静强度工况状态，即车辆沿着良好的路面做匀速直线运动，或处于静止转态。在纯弯曲边界条件中，限制右后方主梁的六个自由度，左前方Y方向自由度释放，右前方Y方向平动。仿真结果如图6所示，从应力云图可知，纯弯曲工况下，最大位移出现在主梁前部，最大应变0.7943 mm，说明在车架在平衡状态时，前部动力引擎部分对车架的载荷影响较大。而在车辆的设计过程中，一般车架弯曲挠度要求控制在10 mm以内 [10] ，这也是为了汽车的安全可靠性考虑，所以仿真结果显示远低于参考值，意味着该变形铝车架总成在抗弯曲性能较为良好。

图7是计算出的等效应力结果。由应力云图可知，纯弯曲工况下，最大应力出现在副驾驶靠背所在的横梁部分，最大应力 ${\sigma }_{\max }=56.16\text{Mpa}$ ，结合位移情况分析可知满载时车辆前部载荷对结构影响最大。代入式 $S={\sigma }_S/{\sigma }_{\max }$ ，可得安全系数S = 8.99远大于1。即该车架有很大的安全裕度，满足强度要求。

Figure 5. Load distribution diagram

图5. 载荷分布示意图

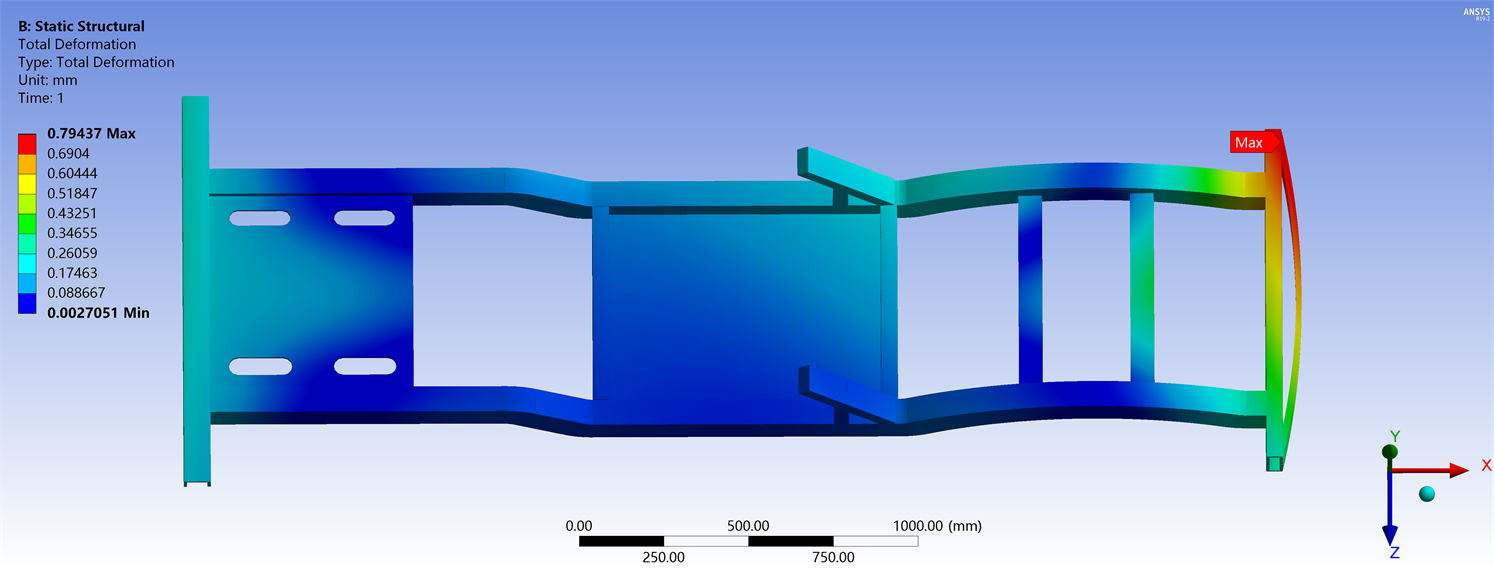
Figure 6. Pure bending total strain cloud map

图6. 纯弯曲总应变云图

Figure 7. Equivalent stress nephogram for pure bending condition

图7. 纯弯曲工况等效应力云图

3.2. 动强度分析

载荷施加与平衡状态工况相同，考虑在车辆在行驶过程中，路过特殊地形导致车轮悬空的情况，车架的支撑状态将发生变化，该扭转模拟轿车在路过坎坷路段时，左前轮与右后轮悬空，释放自由度并为其他两个轮子添加固定支撑，由云图可知，最大位移出现在前部横梁部分，发生4.5146 mm的位移，而后部横梁变形较小，原因是仅固定了右前与左后的车轮，车架在电机、动力电池等其他载荷作用下向下变形，最大变形位置如图8所示，车架各部分变形均小于10 mm，最大应力为120.85 MPa，出现在副驾驶处的横梁部分，计算安全系数为4.2 > 1。综上所述，该模拟工况下应力和应变均满足设计要求。满载扭转工况等效应力如图9所示。

Figure 8. Full load torsional displacement cloud image

图8. 满载扭转位移云图

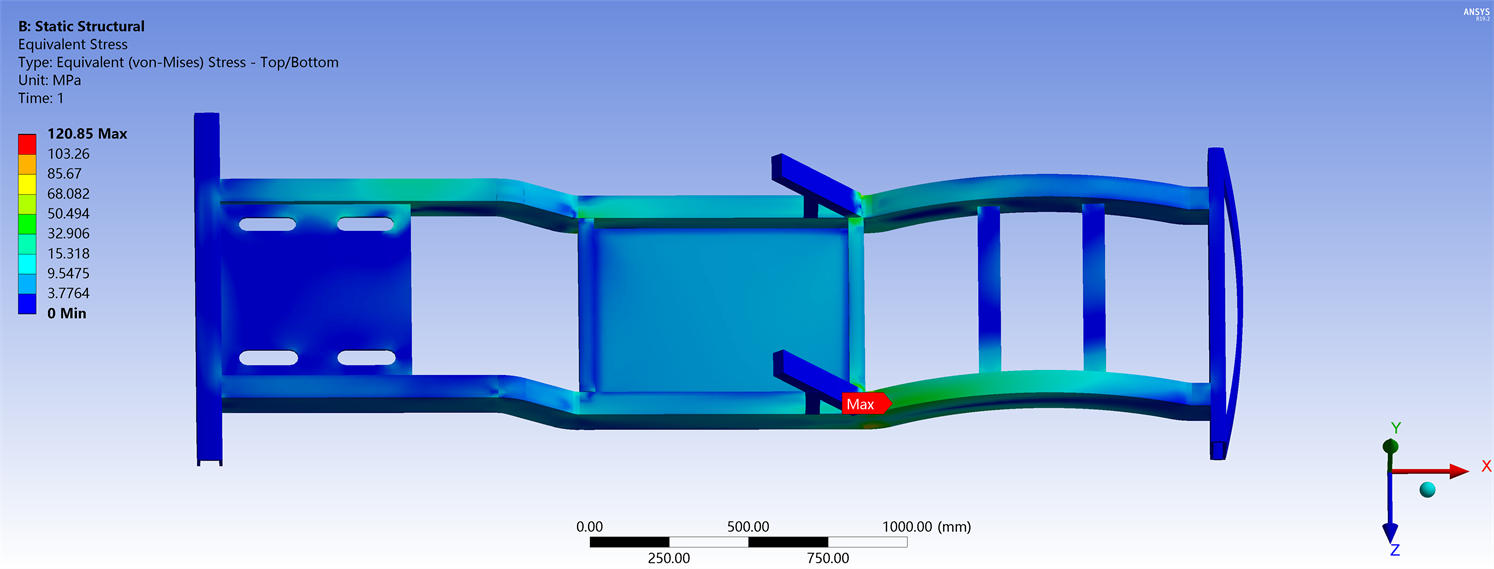
Figure 9. Full load torsional stress nephogram

图9. 满载扭转应力云图

3.3. 扭转刚度分析

扭转刚度的计算方法，在分析车架的扭转刚度时，只保留了重力，在电动机前梁所处位置分别添加2000 N大小相等，方向相反的假定远程作用力，并约束车架后部纵梁及其连接点x，y和z等3个自由度，载荷示意图如图10所示。

扭转刚度的计算方法：

$E=\frac{M}{\theta }=\frac{FL\pi }{180\arctan \left(2/L\right)}$ (1)

Figure 10. Applied force diagram

图10. 施加作用力示意图

式中：M为作用力矩；L为车辆轮距的一半；θ为扭转角度；F为施加的外力。

校核方法：由于本文使用的7系铝合金仍为金属塑性材料，因此依据材料力学第四强度理论作为准则，应力表达式：

${\sigma }_s=\sqrt{\frac{{\left({\sigma }_1-{\sigma }_2\right)}^2+{\left({\sigma }_2-{\sigma }_3\right)}^2+{\left({\sigma }_3-{\sigma }_1\right)}^2}{2}}$ (2)

其中 ${\sigma }_i\left(i=1,2,3\right)$ 为三个定义的主应力， ${\sigma }_s$ 为材料的屈服强度。

由上述分析得F = 2000 N，L = 500 mm，计算出扭转角度为θ = 0.368˚，则车架的扭转刚度为2717.39 N·m/(˚)，由于本文研究的车架是新能源通用车辆上的，依据经验值 [12] ，只要扭转刚度不小于1700 N·m/(˚)就可以认为设计模型的扭转刚度达标。

4. 新能源车架动力学特性分析

4.1. 研究方法

尽管新能源汽车通过电动机替代了传统的燃油机，噪声、振动得到明显的改善，但新型结构的设计仍然需要研究它的固有频率以及整机的共振特性，采用合理的方法研究车架结构的动应力仍然有意义，本文基于计算分析法，对结构进行模态分析，确定了各阶振型，为新能源汽车主梁结构未来设计提供了一定的参考价值。本文在研究过程中考虑到实际工况，利用软件优势构建多自由度弹性系统，依据表达式(3)，求出n个特征解 $\left({\omega }_1^2,u_1\right)$ 、 $\left({\omega }_2^2,u_2\right)$ 、 $\left({\omega }_n^2,u_n\right)$ ，从而得到若干个固有频率和固有振型。

$K{u}_0-{\omega }^{2}M{u}_0=0$ (3)

式中，u为固有振型，ω为固有频率，K、M分别代表车架结构的总刚度矩阵和总质量矩阵。

4.2. 车架自由模态分析

车辆在实际环境下受不同激励源的影响，产生共振将对车架结构产生破坏，存在安全隐患，本文研究了该新能源车架的自由模态，通过Workbench建立分析项目，提取车架的前12阶模态，重点分析了路面及电动机两个激励源的振型影响，如表3总结了该车架各阶模拟频率及振型计算结果。

Table 3. Modal frequency and mode characteristics of frame

表3. 车架模态频率及振型特征

由表3可知，前六阶固有频率较小且远低于路面激励的30 Hz振动频率，且前六阶结构振型特征未发生明显变化，所以可忽略不计。该车架自由模态各阶振型云图如图11至图16所示。

依据仿真结果可以看出，车架第七阶固有频率为40.376 Hz，振型为Y轴负方向的弯曲振动，第七阶振型云图如图11所示，峰值出现在前部横梁区域，并且与车架的实际使用工况接近。

Figure 11. Seventh order mode cloud image

图11. 第七阶振型云图

八阶模态固有频率为64.126 Hz，振型表现为车架两端X轴的反向扭转振动，并呈向腹部递减的状态，第八阶振型云图如图12所示，九阶模态固有频率为72.154 Hz，振型为Z向正方向弯曲振动，变形最大区域出现在车架前部，第九阶振型云图如图13所示，十阶模态固有频率为108.03 Hz，其振型表现为绕腹部的弯曲扭转组合振动，第十阶振型云图如图14所示，十一阶模态固有频率为109 Hz，振型为Y向的弯曲振动，第十一阶振型云图如图15所示，十二阶模态固有频率为159.85 Hz，其振型表现形式与前几阶略有不同，但其中心位置基本没有变化，第十二阶振型云图如图16所示，最大变形出现在电动机固定梁上，最大变形为17 mm左右，七至十一阶每一阶的固有频率在小于40 Hz的范围增加，十二阶模态固有频率最大为159.85 Hz，七至十二阶固有频率范围为40~160 Hz，均大于路面激励的30 Hz。

通过分析车架的前十二阶最大固有频率，结合汽车用电动机转子振动频率的经验值600~5000 Hz，不会产生共振，根据仿真结果，该车架前12阶固有频率均低于电动机转子固有频率，可知车辆在正常行驶过程中，避免了共振现象，验证了该设计结构的合理性。

Figure 12. Mode nephogram of eighth order

图12. 第八阶振型云图

Figure 13. Ninth order mode cloud image

图13. 第九阶振型云图

Figure 14. Mode cloud image of tenth order

图14. 第十阶振型云图

Figure 15. Cloud image of eleventh order mode

图15. 第十一阶振型云图

Figure 16. The twelfth order mode cloud image

图16. 第十二阶振型云图

5. 结论

本文通过Solidworks建立车架模型，并结合有限元分析方法，设计了一种应用7系铝合金材料的新能源轿车车架，重点关注了新研发车架的强度、扭转刚度及可靠性等，分析得出以下结论：

1) 应用的新材料7075铝合金的力学性能优越，满足车架的设计要求，实现了轻量化设计，车架设计质量为113.278 kg，达到减重的目的，但目前材料价格昂贵，随着新材料的普及，具有广阔的发展应用前景。

2) 通过对车架静态特性分析可知，该车架乘员下的横梁部分出现应力集中现象，为后续新能源车架最优设计方案，提供了一定的指导意义。

3) 对车架的模态分析可知，车架虽满足设计要求，但固有频率仍与阶次正相关，寻求一种合理的策略减低车架固有频率并使其收敛，对新型车架的设计方式产生了积极影响。