1. 引言
随着无线通信和定位技术的发展,高精定位系统广泛应用于车辆及智能终端,产生大量的轨迹数据,可用于空间数据挖掘、智能交通、城市计算等领域。由于城市道路情况复杂以及建筑物或隧道遮挡信号等因素的影响,移动目标的定位轨迹通常存在误差,需要运用地图匹配技术将轨迹点匹配到正确的道路上。
地图匹配是通过辅助设施提高定位精度的基本操作,它利用空间道路网络数据(道路中心线)来识别正确的道路及车道,并确定移动目标在道路上的精确位置,从而关联上高精度地图的丰富语义信息。位置传感器生成定位数据的方式,总是包括全球卫星定位系统(GNSS),以及其他传感器和数据,例如里程表、罗盘读数、Wi-Fi基站和移动蜂窝信号。自定位技术和需求问世以来,地图匹配方法已被利用已有多年。
两个主要的错误来源,使地图匹配工作具有挑战性。第一,前期定位结果的准确性始终是所有地图匹配计算上下文环境的核心,例如GNSS定位数据、行人定位导航、手机定位、室内定位。不同传感器的融合定位方式有不同的误差原因。定位误差来源主要包括阻塞信号、信号多路径效应 [1] [2] [3] 和最小覆盖区域定位数据 [4] 。第二、道路交通地图的细节层次和路网拓扑表达。自动驾驶、网联汽车越来越多地采用更精细化的高精度地图——车道级、丰富语义的自动驾驶地图 [5] 。
在本文中,提出了一种基于隐马尔可夫链模型的车道地图匹配算法。该算法采用基于多传感器融合的路侧感知定位数据,和遵循《自动驾驶高级辅助驾驶地图制图规范》的车道级地图数据。
本文组织如下:第1节介绍了地图匹配的背景需求和挑战。第2节简要描述了地图匹配方法和发展趋势。第3节描述了隐马尔科夫链简要介绍和基于隐马尔可夫链模型的地图匹配算法。第4节评估车道级地图匹配算法的测试效果与分析。第5节阐述了分析与展望。
2. 车道级地图匹配方法综述
2.1. 地图匹配方法综述
地图匹配方法综述主要是通过比较匹配算法的准确性和普遍性来进行的,并总结行业潜在需求和数据来源提出的新问题。地图匹配算法使用的信息可分为4类几何策略(如点到点、点到曲线和曲线到曲线等)、拓扑策略(如道路网络中地图要素之间的邻接、连通和包含等关系)、概率策略(如卡尔曼滤波器、模糊逻辑模型、贝叶斯推理及其衍生物)和综合信息。基于几何策略的地图匹配关注的是位置与候选道路链接的距离,以及道路链接与轨迹之间的相似性,主要考虑投影偏差 [6] [7] 。该算法找到靠近定位点的链接和链接中的投影点。它甚至使用两个或多个连续链接的链接方向。这些算法可以通过在交通道路网络上构建四叉树结构来快速获得对象的大规模跟踪结果。当交通道路拓扑复杂时,这些算法会显示出它们的弱点。
基于拓扑策略的地图匹配 [8] 将几何数据和轨迹的拓扑关系(按位置和候选道路链接)视为决策因素。在第一步获得初始匹配后,第二步是从初始匹配中为候选链接赋值。该值取决于以下几个方面:(a) 定位点与链接的接近程度,(b) 连续点与链接的方向之间的相似性以及(c) 链接与“线”之间的相交角度连续的定位点。连续道路链接之间的连通性是这些算法中的建设性约束,特别是当真实轨迹穿过隧道或挤满高层建筑的中央商务区区域时。这些因素构成了具有不同权重的最终分数。从基于拓扑和几何的计算中获得最高分的候选位置被视为车辆的真实位置。基于拓扑策略的地图匹配利用了几何策略,但在低采样率、大规模定位数据或精度低的数据等更复杂的环境中无法产生令人满意的最终结果。
基于概率策略的地图匹配,包括基于HMM的GPS定位地图匹配 [7] [8] ,多重假设 [9] 侧重于所有位置数据和所有候选道路链接的总体情况 [10] ,而不是在各个位置和附近的候选道路链接之间进行计算。这些算法通常需要三个步骤。初始步骤是获取具有松散约束距离的定位点附近的所有链接。这个距离的值取决于交通路网的统计。此步骤确保在第一步中选择真实轨迹,并伴有高冗余。第二步是为每个环节分配一个实用性。与基于拓扑策略的地图匹配的实用性相比,实用性取决于更多的因素,如投影偏差、方向相似性、相交角度和拓扑之间的连通性。第三步是计算每个时间累积的所有链接。基于概率策略的地图匹配方法利用了综合计算的优势,显着增加了计算时间。
2.2. 车道级地图匹配新进展
实时地图匹配则是当前自动驾驶系统的重要需求之一 [11] 。实时地图匹配场景中,难以同时保障算法准确率和时间效率,需要选取合适尺寸的计算窗口。如果计算窗口过小,则算法的准确率较低; 如果计算窗口过大,则匹配计算过程耗时较长。
事实上,地图匹配技术需求,一直对准确度、运行耗时、抗干扰等性能有着较高的需求。随着自动驾驶、智能网联汽车的产业推进,各项算法性能有了更为具体的指向。实时运行计算意味着与车载系统保持同频或更高的频率。随着自动驾驶高精地图的推广,车道级地图成为自动驾驶的标配,这意味着对地图匹配算法提出更高要求。对于不同来源的融合定位结果,如道路交通全息感知系统输出的路侧感知定位信息,要求地图匹配算法具有更强的鲁棒性,对质量较差、频率较低的定位数据,更友好。
只是随着数据的丰富,应用场景更广泛、性能也越来越强,以前看似矛盾的两个诉求(实时性与抗误差干扰),现在能输出能够被(自动驾驶)接受的解。
3. 基于隐马尔科夫链的车道级地图匹配建模
3.1. 整体模型
隐马尔科夫模型是关于(位置、状态、属性等)时序数据的数学模型,描述由一个待求解的马尔科夫链随机生成不可观测的真实状态序列,再构建各状态值及其对应观测值之间的生产概率模型,从而产生观测随机序列的过程。其中,马尔科夫链随机生成的状态序列,视为系统的真实状态,称为状态序列;真实状态与观测值之间,需要构建一个生成规则,而由此产生的观测的随机序列,称为观测序列。
本文提出应用隐马尔科夫链模型,来构建地图匹配的数学模型,见图1。

Figure 1. Framework of lane-scale map matching based on Hidden Markov Model
图1. 基于隐马尔科夫链模型的车道级地图匹配的整体框架
首先,获取当前的组合定位结果,并搜索临近的车道(以车道中心线进行表达),得到集合LaneSet_add。第二步,将得到的车道集合,与历史轨迹对应车道的集合,进行合并,得到当前的状态空间,并更新初始状态。第三步,融合历史轨迹和当前位置,进行自适应的抽稀处理,得到当前的观测空间。第四步,基于网络拓扑属性和空间几何属性,如投影距离、车道连接方式、车道内包含关系等,构建状态转移矩阵。第五步,基于组合定位结果与真实状态(即车道)的映射关系影响因素,主要考虑几何投影距离,计算定位与道路的映射概率,构建生成概率矩阵。第六步,基于隐含状态最大概率链计算方法,求解隐马尔可夫链模型,输出最匹配的状态序列,即车道序列。第七步,基于车道级路网的拓扑关系,复原行车路线和实时轨迹,并更新初始状态、历史轨迹的投影位置,及其对应车道集合。
3.2. 自适应的状态空间
基于贝叶斯网络的理论,结合道路交通地图的网络特征,越是相邻近的节点,对当前节点匹配计算过程的影响越重要。自适应抽稀处理,就是从最近期发生的时间和信息中,抽取能代表过去时间序列状态的特征值,参与到当前时刻的地图匹配计算。抽稀方法是通过经典的反距离平方法,对过去时间序列的状态,进行赋予不同的权重。时间越临近的状态,其影响权重越大;时间越远的状态,其影响权重越小。因此,越是邻近的区域,取点越多,越密集。
同时,考虑到观测空间的维度是影响计算耗时、匹配时效性的重要因数,因此,由于对抽取的轨迹点数,在不影响传递概率计算异常(如计算不收敛)的条件下,越小越好。
本方法构建了一个自适应的观测空间计算方法,在邻近区域抽取更多的轨迹点,并且轨迹点数整体抽取比例依据轨迹序列的特征,进行动态调整。如图所示,圆点代表的是行车的轨迹,最右侧是当前时刻
。
从
时刻,向过去追溯,追溯长度为过去4条车道对应的长度。追溯得到的轨迹,就是当前时刻匹配计算的有效轨迹,其长度为s。因此,s值是动态变化的。对应的,分界线之外的轨迹,则是当前时刻匹配计算不考虑的轨迹区域。
在有效轨迹区域内,经过上述的抽稀处理,得到反应状态-观测概率模型特征的轨迹数据,表达为绿色圆点。抽稀后的轨迹,及其对应的车道,就是经过自适应计算的观测空间和状态空间,见图2。
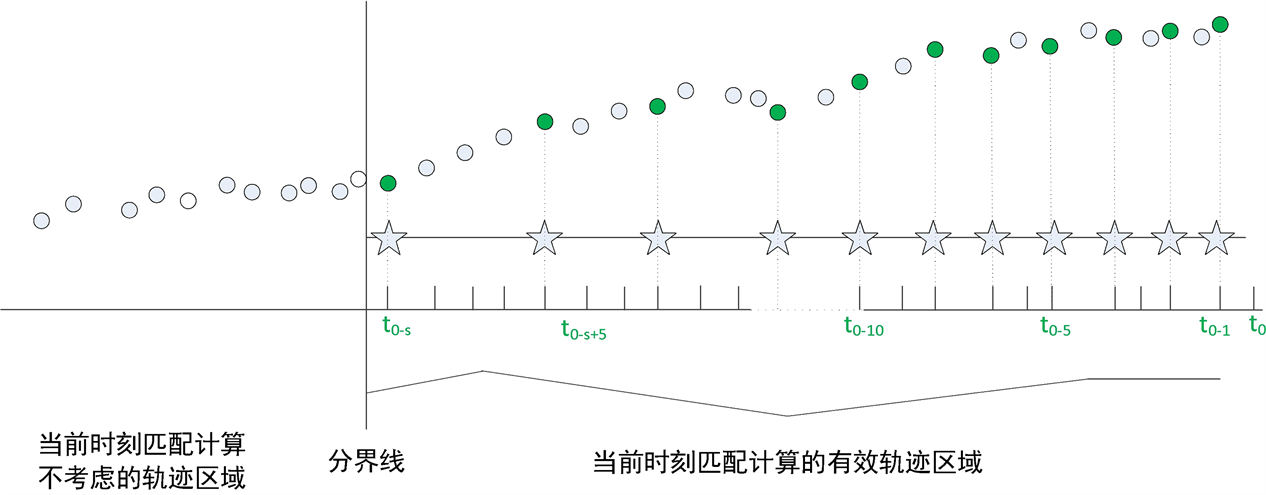
Figure 2. Process of self-adapting calculation to extract observation state
图2. 自适应状态观测空间抽取计算过程
其中,
是当前时刻;
是历史时刻;绿色圆点是抽稀的观测空间;车道则是自适应计算后的状态空间。
3.3. 动态构建状态转移概率
拓扑关联是指道路交通路网中道路、车道、车道组、车道分界线等线目标之间的关联关系。车道级地图匹配计算过程,主要考虑车道、车道组的拓扑关联。首先,基于当前车道所在车道组的几何关系,搜索前后车道组,即与当前车道组有共同端点的车道组。再通过车道的属性值来查询,车道内的所有车道。
因此,当前车道转向其他车道的情景分2类:
· 从当前车道转向相同车道组其他车道;
· 从当前车道转向相邻车道组的车道;
基于几何关系,即轨迹点的平均间距与车道线的平均长度之比,近似得到轨迹点所在车道的转换关系,本方法在此采用如下定义:
· 从当前车道转向相同车道组,概率总和为
;其中,留在当前车道的概率为
,转向同一车道组内其他车道的概率和为
;
· 从当前车道转向相邻车道组的车道,概率总和为
;
计算公式表达为如下,其中,
是第i个车道中心线对象,
是从车道
转到车道
的概率。
经过路网特征统计,包括车道线对象的长度、定位轨迹的间距特征,在下述计算中,取
,
。
如图所示,图3表示与当前车道所在车道组下游直接连接的4个车道组。图4表示当前车道组直接接连的车道组,及其所包含的车道。

Figure 3. Connection between current lane set and in-depth lane set
图3. 当前车道组与下游车道的关联关系

Figure 4. Lane set connected with current lane set
图4. 当前车道组直接相连的车道组
3.4. 动态构建发射概率
发射概率主要是表达的是从在某个观测状态下,映射到某个具体状态的概率。在地图匹配中,则表达为,某个轨迹点,映射到交通路网中某条车道的概率。基于地理学第一定律——任何事情,距离越近,关系就越紧密,影响该概率值的主要因素是轨迹到车道的距离。考虑到组合定位的质量特征,本方法中,反距离计算采用二次开方的结果,发射概率计算方式如下:
其中,
是第i个车道中心线对象;
是第t个观测值;k是当前时刻状态空间的维度,即共有k个车道;
附近的第t个观测值;
是从观测值
发射到车道
的概率。
3.5. 隐含状态序列最大概率计算
在求解隐含状态序列阶段,本文采用维特比数学模型。维特比算法(vibertalgorithm)是一种动态规划算法。它用于寻找最有可能产生观测事件序列的维特比路径——隐含状态序列,就是求所有观测序列中的最优。
通过构建观测空间、状态空间、初始状态、状态转移概率矩阵、发射概率矩阵等模型参数,进行动态规划迭代计算,解算隐含状态序列链的最大概率。
其中,
是第i个时刻的状态;
是第i个观测值;
是初始状态;
是从
状态转移到
状态的概率;
是在
状态下,得到观测值
的概率。通过维特比算法,对上述公式,进行迭代计算,得到隐含状态序列最大概率值。
4. 测试与分析
4.1. 测试区域和数据集介绍
本文所述实验过程,其测试区域位于浙江省杭州市的智能网联汽车测试道路。该测试区域覆盖开阔道路、高楼遮挡道路、立交桥道路等道路场景。
本次地图匹配工作仲,道路路网数据采用shapefile格式,制图规范遵循《自动驾驶高精地图制图规范》。道路交通路网数据的整体精度,水平方向上优于0.1 m。道路路网整体覆盖10,267条车道线/48,632车道组。每条车道组包含1~N条车道,其中车道以车道中心线来表达。
地图匹配工作的另一组数据是移动目标的运动轨迹时间序列。移动目标遵循道路交通规则,运动速度小于80 km/h。本次测试,采集的运动轨迹数据,其原始频率是5 Hz,其定位精度在水平方向上优于0.1 m。
4.2. 测试结果分析
为了验证本文所述地图匹配算法的准确率和鲁棒性,本文对组合定位轨迹数据进行时间降频和主动添加误差等处理,得到4组数据,并得到不同的性能统计,详见表1。
原始的组合定位数据,频率是5 Hz,平均定位偏差优于0.1 m。基于原始数据的测试,匹配准确率,在测试区域全部路段上,达到了100%,水平偏差为0.267 m。将原始定位数据进行抽稀处理,进行地图匹配验证,地图匹配的准确率为98.71%,水平偏差为0.293 m。准确率的下降,主要出现在切换车道、拐弯时偏离默认车道等情景。进一步,将定位数据主动添加1 m以内的随机误差,并进行地图匹配验证,地图匹配的准确率为96.26%,水平偏差为0.824 m。随着组合定位的随机位置偏差扩大至1.5 m时,准确率和位置偏差均出现了不断恶化的情景,甚至当随机位置偏差继续扩大至2 m时,准确率和偏差出现了较大幅度的下降,表明此时的位置偏差已经使得地图匹配算法不再适用。

Table 1. Performance comparison of lane-scale map matching for data with different frequency and accuracy
表1. 对不同精度和频率的定位数据进行车道级地图匹配的性能对比
5. 分析与展望
无人驾驶系统依赖高精度的环境感知和自主定位导航技术。地图匹配长期伴随无人驾驶定位导航技术,从早期的浮动车定位、单传感器定位、GNSS + IMU组合定位、多传感器融合定位,用于修正提升定位质量。本文提出基于隐马尔科夫链的车道级地图匹配技术,进一步提升了地图匹配的定位精度,并且从构建自适应的状态空间、观测空间等手段去提升隐马尔科夫链在实时地图匹配上的计算性能。
本文认为,车道级地图匹配的未来发展重点应围绕以下三个方面:
1) 完善自动驾驶地图制图规范以及编解码方面的标准化,从而提升车道级地图匹配算法的计算性能,并促进地图匹配技术在智能终端中的落地应用;
2) 通过道路路网拓扑关联和其他约束,提升状态空间、观测空间、状态转移模型等参数计算的自适应性,从而提升算法模型的鲁棒性;
3) 进一步测试不同定位精度下,应用隐马尔科夫链模型的地图匹配的算法性能,以便在定位质量受到干扰时,对地图匹配计算过程和结果,进行增强处理。
NOTES
*通讯作者。