第一性原理研究ZrO₂晶体中的氧填隙

Study on the Oxygen Interstitial in ZrO₂ Crystals with First-Principles

摘要: 本文利用第一性原理研究了单斜相结构ZrO₂晶体中氧填隙O_i对晶体结构，电子结构和光学性质的影响。利用广义梯度近似GGA结合PBE交换泛函计算的带隙严重低于实验值，无法获取准确的缺陷转化能级。本文结合Alkauskas提出的带边修正的方法，采用杂化泛函的方法获取更准确的电子能带结构。采用有效尺寸修正(FNV)方案消除，由于引入周期性边界条件，带电缺陷间的不可忽视的自相互作用。通过以上的修正，我们可以得到准确的缺陷形成能和缺陷转化能级。通过一维位形坐标探究电子跃迁的过程以及能量的变化，基于Frank-Condon原理方法给出归一化的光谱线形图。计算得到 和 的吸收谱分别位于8.69 eV和7.06 eV，而发射峰位置分别位于5.20 eV和5.52 eV。氧填隙的吸收峰和发射峰均在紫外区。

Abstract: The effects of oxygen interstitial O_i in monoclinic ZrO₂ crystal on the crystal structure, electronic structure and optical properties have been studied by First-Principles. The band gap calculated by generalized gradient approximation GGA combined with PBE exchange functional is seriously lower than the experimental value, and the accurate defect transformation level cannot be obtained. In this paper, combining the method of band edge modification proposed by Alkauskas, a hybrid functional method is used to obtain more accurate electronic band structure. The effective size correction (FNV) scheme is used to eliminate the non-negligible self-interaction between charged defects due to the introduction of periodic boundary conditions. Through the above correction, we can get the exact defect formation energy and defect transformation energy level. The process of electron transition and the change of energy are investigated by one-dimensional configuration coordinates, and the normalized spectral line diagram is given based on the Frank-Condon principle method. The calculated absorption spectra of and are 8.69 eV and 7.06 eV respectively, and the emission peaks are 5.20 eV and 5.52 eV respec-tively. The absorption and emission peaks of oxygen interstitial are both in the ultraviolet region.

1. 引言

二氧化锆(ZrO₂)是一种很有前途的宽带隙金属材料，由于具有良好的光学和物理性能，如高折射率、高介电常数、高强度和韧性等，受到了广泛的关注 [1] [2] 。ZrO₂已广泛应用于催化剂、光学玻璃、热涂层、光子器件等领域 [3] [4] [5] [6] [7] 。ZrO₂具有较宽的带隙，是一种具有良好光学应用前景的发光材料。因此，我们着重研究了基于电荷跃迁能级的ZrO₂晶体的光学性质。

ZrO₂是一种多晶相转换氧化物材料，在常温下仍保持三种晶格结构，在低温下为单斜(m)相(空间群P21/c)，在1400 K以上为四方(t)相(P42/nmc)，在2570 K以上为立方(c)相( $\text{Fm/}\bar{3}\text{m}$ )。一般情况下，随着温度的升高，ZrO₂的相会发生变化。ZrO₂在室温下存在于单斜相中，而立方相可以通过 ${\text{Ca}}^{\text{2+}}$ 、 ${\text{Mg}}^{\text{2+}}$ 和 ${\text{Y}}^{\text{3+}}$ 等阳离子的掺杂而稳定 [8] [9] [10] [11] [12] 。

经过各种实验和验证 [11] [13] [14] ，发现在纯ZrO₂晶体中掺杂Ti使其发光 [15] 。自由电子被 ${\text{Ti}}^{\text{3+}}{\text{/Ti}}^{\text{4+}}$ 电荷补偿产生的氧空位(f++中心)捕获。在室温下，氧空位被认为是电子的深陷阱，它可以使未掺杂的ZrO₂持续发光 [16] 。此外，张景吉 [17] 还发现氧缺陷可以提高可见光光催化降解有机污染物的能力。在吸收带边缘的末端引入氧空位是一种有效的策略，因为ZrO₂晶体在可见光区域的吸收和发射峰与氧空位有关。该晶体在富氧条件下，很容易形成氧填隙，氧填隙的存在影响了该晶体的光学性质，而目前对氧填隙的研究还很少，所以，本文将对氧填隙进行系统研究，研究结果有利于该晶体的实际应用。

本文通过对完整晶体的基本性质以及含有氧填隙的晶体进行研究。为了解决密度泛函理论计算的带隙偏小以及带边不准确等问题，使用杂化泛函计算(HSE)修正DFT [18] [19] 计算的价带顶以及带隙。使用FNV修正消除带电缺陷在周期边界条件下的自相互作用，得到比较精确的缺陷转变能级。在缺陷转变能级得到有效修正的基础之上结合电子声子耦合进一步计算带电氧填隙的光谱。

2. 计算模型和方法

在本文当中所有的计算都是基于DFT [20] [21] ，在VASP计算模拟软件中实现 [22] [23] [24] 。用投影缀加波(PAW)方法描述离子与价层电子轨道间的相互作用，用广义梯度近似(GGA)结合平面波赝势(PBE)处理交换相关函数。选取ZrO₂晶体结构中的单斜相(m-ZrO₂)，将12个原子的原胞结构扩展为96个原子的超晶胞(2 × 2 × 2)，在此基础上构建缺陷模型。Zr和O原子的价电子构型分别为4s2，4p6，5s2，4d2 and 2s2，2p4 [25] 。晶格常数为a = 10.37297 Å，b = 10.49702 Å，c = 10.74065 Å。首先通过MedeA软件对含有本征点缺陷的计算模型进行严格的结构收敛性测试，优化收敛的标准是能量误差小于1 × 10⁻⁵ eV/atom [26] ，结果均为收敛。经测试后平面波的截断能设为600 eV，布里渊区中倒格子k点设为3 × 3 × 3。

氧填隙模型则是通过MedeA软件寻找结构中最佳填隙位置，即能量最低结构最稳定的位置，添加一个氧原子形成97个原子的计算模型结构。如图1所示。在坐标(0.8893, 0.5581, 0.6514)处添加一个原子形成氧填隙为−2价，在本文中将研究带有电荷0、−1和−2三种缺陷结构。

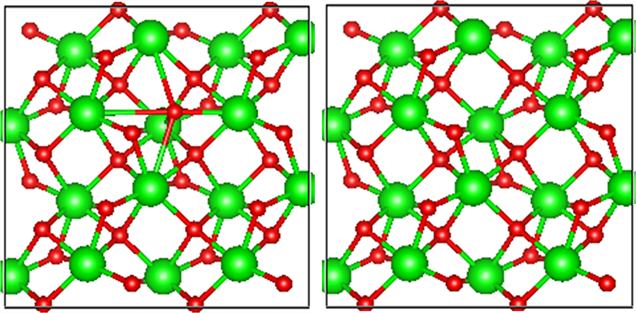
Figure 1. (a) A supercell containing oxygen interstitial (b) A complete crystal supercell with Zr atoms represented in green and O atoms represented in red

图1. (a) 含有氧填隙的超晶胞，(b) 完整晶体的超晶胞，绿色代表Zr原子，红色代表O原子

3. 计算结果和讨论

3.1. 缺陷形成能修正

晶体中点缺陷的缺陷形成能可通过以下公式确定 [27] ：

$E_f\left(D^q\right)=E\left(D^q\right)-E\left(perfect\right)+{\displaystyle \sum n_s{\mu }_s}+q\left(E_{Fermi}+{\epsilon }_{vbm}-\Delta V\right)-E_{corr}$ (1)

前两项分别是结构优化后的完整ZrO₂晶体中基于DFT计算的含有缺陷和不含缺陷的总能量。 ${\displaystyle \sum n_s{\mu }_s}$ 在本文表示氧的化学势。q指缺陷结构所带的电荷， $E_{Fermi}$ 表示相对于价带顶(VBM)的费米能级。 ${\epsilon }_{vbm}$ 是计算完整超晶胞所对应的VBM，ΔV是完整超晶胞和含有缺陷超晶胞之间的平均静电势差。等式的最后一项 $E_{corr}$ 是有限尺寸校正。本文采用Freysoldt，Neugebauer和Van deWalle提出的FNV修正方法对带电缺陷形成能进行了修正。

在完成FNV修正的基础上，通过公式(1)计算得到缺陷形成能。如表1所示，氧填隙带不同电荷修正前和修正后缺陷形成能之间的比较。结果表明，FNV修正后缺陷形成能的误差在0.3~1.3 eV范围内。同时在表中也能注意到，高价态的缺陷形成能较高。

Table 1. Different valence defect formation energy of oxygen interstitial gap (Fermi level is set at the top of valence band under hypoxia condition)

表1. 氧填隙不同价态缺陷形成能(缺氧条件下，费米能级设置在价带顶)

3.2. 带边修正

当缺陷存在不同价态时，缺陷转化能级即为缺陷形成能相等时所对应的费米能级，如(2)式所示。

$\epsilon \left(q_1/q_2\right)=\frac{\Delta E_f\left(\alpha ,q_1\right)-\Delta E_f\left(\alpha ,q_2\right)}{q_1-q_2}+{\epsilon }_{VBM}$ (2)

式中， $\Delta E_f\left(\alpha ,q_1\right)$ 和 $\Delta E_f\left(\alpha ,q_2\right)$ 分别表示缺陷 $\alpha$ 处在q₁和q₂价态时的缺陷形成能(费米能级设在价带顶)， $\epsilon {}_{VBM}$ 表示带边修正的价带顶的差值 [28] 。

基于DFT-GGA近似方法的计算，存在着众所周知的带隙问题，也影响了禁带中缺陷转变能级的计算。为了解决这一问题，对于缺陷的研究从半局域近似到密度泛函理论投入大量的精力，对于应用在小的体系，也探索出几种实用的方法，例如：剪刀–算子法、标记法等等，但是这些方法的普遍适用性不是很明确，近几年，混合密度泛函方法在处理缺陷能级问题上变得越来越适用，在Perdew、Burke和Ernzerhof (PBE)提出的广义梯度近似下，进行了半局域密度泛函计算。其中用Hartree-Fock代替25%的PBE交换能，计算结果有更高的精度和更准确的带隙。

通过GGA-PBE计算获得的带隙为3.61 eV，比实验带隙小2.20 eV。因此，多粒子系统的激发态和带隙中缺陷能级的位置是不准确的。因此应用更精确的混合密度泛函来修正，采用HSE方法来处理交换相

关能修正带边问题，可以由 [29] [30] 给出： $E_{XC}^{HSE}=\alpha E_{XC}^{HF}+\left(1-\alpha \right)E_X^{PBE}+E_C^{PBE}$ 。

通过调整 $\alpha$ 值来实现改变带隙，在这项计算中 $\alpha$ 设置为0.23。 $E_{XC}^{HF}$ 表示Hartree-Fock交换相关能的短程势。 $E_X^{PBE}$ 表示PBE交换能。 $E_C^{PBE}$ 表示PBE相关能。通过HSE方法计算的带隙(5.82 eV)非常接近实验值(5.83 eV) [31] ，带隙值见表2。

Table 2. Calculated bandgap values and experimental bandgap values

表2. 计算带隙值与实验带隙值

Alkauskas等人发现 [32] ，使用相同的赝势，由DFT和HSE计算得出的缺陷转变能级的偏差可以小到0.2 eV以内。

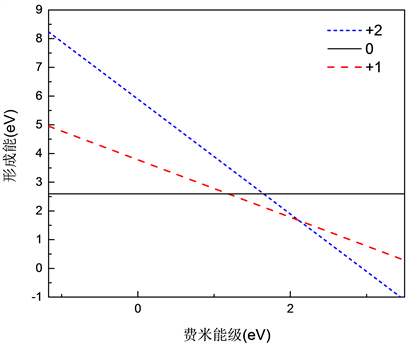
Figure 2. Relationship of oxygen interstitial defect formation energy with Fermi level

图2. 氧填隙缺陷形成能随费米能级的关系

图2画出了不同价态氧填隙缺陷形成能随费米能级的关系图，从图中可以看出，当费米能级靠近价带顶的时候，0价结构的氧填隙 ${\text{O}}_{\text{i}}^{\times }$ 缺陷形成能最低，容易形成，而靠近倒带底时则是 ${\text{<msup> O <mo> ″ </mo> </msup>}}_{\text{i}}$ 缺陷较容易形成。之后根据公式(2)计算相对于价带顶的缺陷转化能级，如表3所示。修正前后的氧填隙缺陷转化能级在禁带中的位置如图3所示。

Table 3. Thermodynamic transition energy levels of interstitial oxygen in different valence states

表3. 不同价态的氧填隙热力学跃迁能级

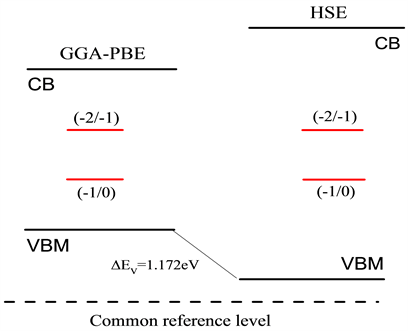
Figure 3. Position of defect transformation energy level of oxygen interstitial in band gap

图3. 氧填隙在禁带中缺陷转化能级的位置

3.3. 光学性质计算

本文介绍了带边修正方法以得到更为准确的能带结构以及缺陷转化能级，介绍了FNV修正方法用来修正带电缺陷带来的静电相互作用，以得到比较准确的缺陷形成能。在得到上述结果后，本文基于位形坐标图研究对应缺陷的光谱。

位形坐标模型 [33] (Configuration Coordinate)是关于电子和离子晶格振动总能量与离子平均位置(用一个坐标表示)相关的物理模型。如图4所示，我们给出了位形坐标模型与吸收和光发射过程示意图，简单描述电子–声子耦合过程，并给出一些相关参数 [34] 。

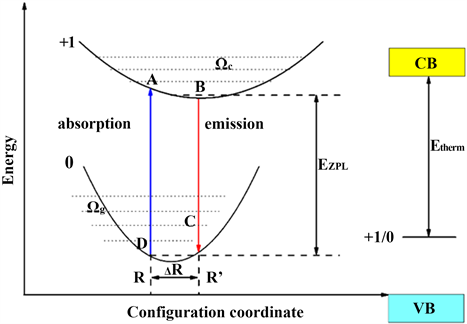
Figure 4. Schematic diagram of configuration coordinate model and absorption and light emission process

图4. 位形坐标模型与吸收和光发射过程示意图

如图4所示，假设费米能级在导带底，其中标0的抛物线表示缺陷的基态，标+1的抛物线表示缺陷的激发态。当电子由基态平衡点R0受到激发后吸收能量被激发到激发态A点，原本的缺陷由于丢失一个电子而无法保持电中性，从而变成+1价。弗兰克–康登原理(Franck-Condon approximation) [33] [34] [35] 与吸收和发射的斯托克斯频移中提到：由于电子的质量比离子的质量小得多，所以在电子跃迁的瞬间，离子来不及调整自己的位置，晶体的位形不变，所以在电子跃迁的瞬间，只是体系的电子价态发生改变，而结构状态依然保持不变。电子由基态到激发态的过程即为光吸收的过程。被激发到激发态的电子由于其不稳定性，必须调整自己的位置以便重新达到平衡，即回到图4所示的B点，这一过程称为晶格弛豫。晶格弛豫过程中产生的能量损耗 $\Delta E_e$ 称为Franck-Condon位移。图4中的 $E_{ZPL}$ 为基态与激发态平衡位置之间的能量差。由示意图可知，光吸收能可表示为：

$E_{abs}=E_{ZPL}+\Delta E_e$ (3)

与光吸收过程类似，光发射过程为：处在激发态B位置的电子会竖直沿着BC线段跃迁到基态势能曲线的C点，然后通过晶格弛豫回到基态平衡位置R₀，这一过程中发射出一个光子，并伴随着能量损耗 $\Delta E_g$ 。由以上分析可以知道，电子在基态和激发态都会发生晶格弛豫，从而产生能量损耗，把这个能量损耗称之为斯托克斯红移(Stokes-shift)。由示意图可知，斯托克斯红移即为光吸收和发射之间的能量差，可表达为：

$E_{abs}-E_{em}=\Delta E_e+\Delta E_g$ (4)

有效参数∆Q表示处于基态与激发态上的每个原子的相对原子质量与其在各个方向上产生的位移乘积的和，可以表示为：

${\left(\Delta Q\right)}^2={\displaystyle {\sum }_{\alpha ,i}{m}_{\alpha }^{1/2}\Delta R_{\alpha ,i}}$ (5)

$\Delta R_{\alpha ,i}$ 表示弛豫过程中的原子在各个方向(i (x, y, z))上产生的位移。其中 $\alpha$ 表示原子种类， $m_{\alpha }$ 表示 $\alpha$ 原子的相对原子质量，∆Q可以表示为：

$\Delta Q=M^{1/2}\Delta R$ (6)

上式中的∆R可以表示为：

${\left(\Delta R\right)}^2={\displaystyle {\sum }_{\alpha ,i}\Delta R_{\alpha ,i}^2}$ (7)

想得到材料缺陷的光谱需要给出电子–声子相互作用的大小。为此，引入黄昆因子(Huang-Rays factor) [36] 这个物理量，该物理量表示晶格弛豫能所折合的声子数，可以定义为：

$S_g=\frac{\Delta E_g}{\hslash {\omega }_g};S_e=\frac{\Delta E_e}{\hslash {\omega }_e}$ (8)

上式中， ${\omega }_g$ 与 ${\omega }_e$ 分别表示基态与激发态的晶格有效振动频率。

在上文中引入黄昆因子S，更好地理解电子–声子耦合作用，并对光学过程中参与的声子数进行量化处理。继而根据弗兰克–康登原理，基于一维位形坐标图讨论了光吸收和发射进程以及涉及到的一些重要参数。我们将更加详细地讨论吸收和发射过程并给出归一化的光谱图。基于第一性原理计算的归一化的发射光谱可以表达为 [34] [35] [37] ：

$L\left(\hslash \omega \right)={\displaystyle \underset{n}{\sum }{\text{e}}^{-s}\frac{s^n}{n!}{g}_{\sigma }\left(E_{ZPL}-\hslash {\omega }_{gn}-\hslash \omega \right)}$ (9)

上式中， $L\left(\hslash \omega \right)$ 是归一化函数，S代表黄昆因子， $g_{\sigma }$ 为高斯函数， $\sigma$ 表示高斯函数展宽因子， $E_{ZPL}$ 表示零声子线。

类似地，我们在假设相同频率的简谐振子的情况下可以得到归一化吸收强度，吸收谱的表达式 [34] [37] ：

$f\left(h\nu \right)={\displaystyle \underset{p=-\infty }{\overset{\infty }{\sum }}\delta \left(E_0-p\hslash \omega -h\nu \right)W_p}$ (10)

上式中， $W_p$ 可以表达为：

$W_p=\exp \left[-\left(2\bar{n}+1\right)S\right]{\left[\left(\bar{n}+1\right)/\bar{n}\right]}^{p/2}\times I_p\left(2S{\left[\left(\bar{n}+1\right)\bar{n}\right]}^{\frac{1}{2}}\right)$ (11)

$I_p$ 是一个修正的贝塞尔函数，上式中， $\bar{n}$ 被定义为：

$\bar{n}={\left[\exp \left(\hslash \omega /kT\right)-1\right]}^{-1}$ (12)

S表示黄昆因子，可由 $S=\frac{\Delta E}{\hslash \omega }$ 获得，k表示玻尔兹曼常数，T表示温度， $E_0$ 表示热跃迁能级(相对于CBM)，它的值等于 $E_{ZPL}$ 的数值， $\hslash \omega$ 表示声子能量， $h\nu$ 表示光子能量，ΔE表示基态或激发态弛豫能。 $\omega$ 表示有效振动频率。

通过电子声子耦合获取受主缺陷氧填隙的光谱，氧填隙在禁带中俘获空穴的跃迁形式以一维位形坐标图来描述，如图5所示。

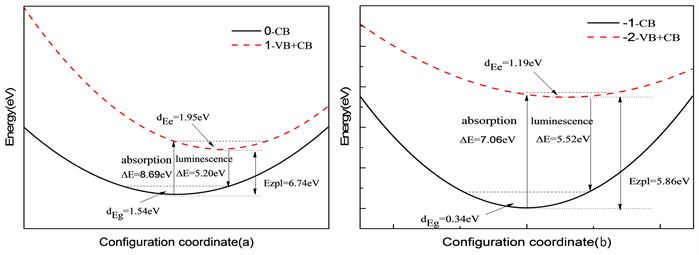
Figure 5. Configuration coordinates between (a) ${\text{O}}_{\text{i}}^{\times }$ and ${\text{<msup> O <mo> ′ </mo> </msup>}}_{\text{i}}$ , and (b) ${\text{<msup> O <mo> ′ </mo> </msup>}}_{\text{i}}$ and ${\text{<msup> O <mo> ″ </mo> </msup>}}_{\text{i}}$

图5. (a) ${\text{O}}_{\text{i}}^{\times }$ 和 ${\text{<msup> O <mo> ′ </mo> </msup>}}_{\text{i}}$ ，(b) ${\text{<msup> O <mo> ′ </mo> </msup>}}_{\text{i}}$ 和 ${\text{<msup> O <mo> ″ </mo> </msup>}}_{\text{i}}$ 之间位形坐标图

通过上图可以看出，氧填隙的晶格弛豫能很大，对周围原子成键情况影响也很大。而且通过表4中氧填隙光谱基本参数可以知道，黄昆因子也很大，氧填隙周围原子晶格畸变较大，证明氧填隙引起了大的晶格畸变。

Table 4. Basic parameters of oxygen interstitial spectrum

表4. 氧填隙光谱基本参数

计算得到了归一化吸收谱和发射谱图，氧填隙的吸收谱和发射谱如图6和图7所示。 ${\text{<msup> O <mo> ′ </mo> </msup>}}_{\text{i}}$ 和 ${\text{<msup> O <mo> ″ </mo> </msup>}}_{\text{i}}$ 的吸收谱分别位于8.69 eV和7.06 eV，对应波长为142 nm和175 nm。而发射峰位置分别位于5.20 eV和5.52 eV，对应的波长为238 nm和224 nm附近。两种价态的斯托克斯位移分别为3.49 eV和1.53 eV。吸收和发射的峰位置都低于400 nm，处在紫外区。按照缺陷转化能级预测 ${\text{<msup> O <mo> ″ </mo> </msup>}}_{\text{i}}$ 发射分支应该小于 ${\text{<msup> O <mo> ′ </mo> </msup>}}_{\text{i}}$ 的发射峰值，但在这里却是相反的，我们可以猜测是由于 ${\text{<msup> O <mo> ′ </mo> </msup>}}_{\text{i}}$ 的晶格畸变较大，导致晶格损耗的能量过大，影响了发射峰值。

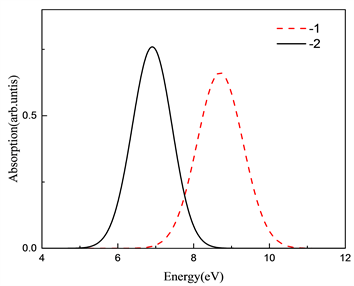
Figure 6. Absorption spectra of different valence states of oxygen interstitial

图6. 氧填隙不同价态的吸收谱

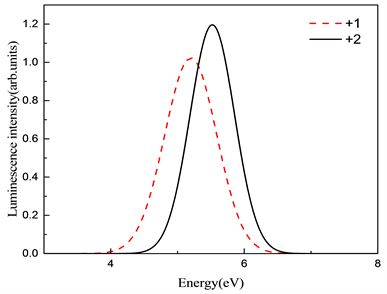
Figure 7. Emission spectra of different valence states of oxygen interstitial

图7. 氧填隙不同价态的发射谱

4. 结论

本文基于第一性原理计算结合GGA + PBE方法计算了ZrO₂晶体中氧填隙的缺陷形成能，结合HSE修正与FNV方法修获取更为精确的缺陷转化能级和缺陷形成能，之后根据一维位型坐标图等讨论其光学性质，最后进行归一化计算吸收谱和发射谱线形图。 ${\text{<msup> O <mo> ′ </mo> </msup>}}_{\text{i}}$ 和 ${\text{<msup> O <mo> ″ </mo> </msup>}}_{\text{i}}$ 的吸收谱分别位于8.69 eV和7.06 eV。而发射峰位置分别位于5.20 eV和5.52 eV。两种价态的斯托克斯位移分别为3.49 eV和1.53 eV，均处在紫外区。本文的结果也可以为实验研究光谱的来源提供理论借鉴。

NOTES

^*通讯作者。