1. 引言
目前各洗扫车厂家的高压水路系统的结构设计都很相似,但是每家的扇形喷嘴都大相径庭,喷嘴受到射流角度、射流距离、流量、压力及车速的变化会产生较大差异,并导致作业后路面的洁净率有较大不同。研究表明,优化喷嘴射流参数,提升喷嘴打击力效果,是提升洗扫车作业洁净度的一条重要途径。
本文对扇形喷嘴内部结构参数研究,包括:V型切槽角度的影响,V型切槽偏移量的影响,出口段长径比的影响,入口压力的影响。对以上因素进行Fluent模拟仿真,找出最优的结果。设计出一款清洗效果好的喷嘴。
为了更有效地提升扇形喷嘴的清洗性能,众多学者对扇形喷嘴进行了研究。周慧宇 [1] ,基于Fluent数值分析软件,建立扇形喷嘴的三维数学模型,研究人字型两段收缩角比值、U形槽半径、出流口长短径之比和切槽深度对扇形喷嘴射流性能的影响规律,并通过实验对模型进行验证。在不同收缩角比值情况下,收缩角比值为4:10时最大动压为116 Kpa,在不同切槽半径的情况下,切槽半径为4 mm时最大动压为107 KPa;在不同出流口长短径比值的情况下,冲击中心点动压无明显变化,剪切层动压随着长短径比值增加而增大,在不同切槽深度情况下,冲击中心点动压无明显变化,剪切层动压随着切槽深度增加而增大。谢飞 [2] ,通过Solidworks软件建立不同结构参数的轴向扇形喷嘴几何模型,分别在Fluent软件中设置参数后,对射流内外流场的速度和含水率进行数值计算。喷射角为65˚,等效直径为2 mm的轴向扇形喷嘴,在射流压力为11 MPa、靶距为90 mm时,更适合贻贝外壳的射流清洗。王功 [3] ,针对飞机发动机在翼水洗专用扇形喷嘴,采用标准k-ε湍流模型,对数种不同的喷嘴和喷嘴外部两相流射流进行建模并仿真。仿真结果显示了喷嘴内部几何形状对射流的中心速度、形状等参数的影响规律。研究发现:喷嘴腔的形状不影响射流形状及速度,射流形状主要由切槽截面角度和偏移量决定,喷嘴输入压力与射流中心速度成正比,对射流形状没有明显影响。李铮 [4] ,对清扫车在清洗过程中残留的水印提出改进方案,在喷头喷射的时候,相连的两个喷头喷射的区域会有重合的部分,在清洗过后会残留水印,洗扫车作业过程中有水的参与,残留痕迹不可避免,但要尽可能地降低水印对清扫效果产生的负面影响。通过增加蓄能器减少高压水路系统脉动,稳定水路系统压力,消除压力脉动,减小水帘搭接长度,可以直观有效地降低水印的宽度。改善最外侧无搭接水帘的喷射角度,降低水平分速度,可以减少水的外溢从而减小最外侧水印的效果。刘洋 [5] ,针对洗扫车所需的高压水泵的流量和工作压力,对水泵进行合理选型,并根据水泵流量与管路压力损失的关系,介绍了选择管路内径的方法,对不同作业模式下清洗喷杆的布置和喷嘴参数选定进行了分析,在流量控制设计上提出了一种通过合理地减少水流量来延长作业时间和提高清洗效率的改进方案。崔少晨,柴立 [6] ,对洗扫车的清洗系统设计进行了研究,包括高压喷嘴的选型、高压喷管的设计计算顿号以及最大流量计算。在此基础上对高压水泵进行选择,从而在通过调节安全阀、液控溢流阀等的压力阈值来保证系统的正常工作压力的前提下,结合电气系统、气动系统控制气动高压球阀来实现高压水路系统的不同工作模式的切换。
2. 水射流参数理论计算
对于连续水射流,如何高效进行切割、清洗等工作,其关键点在于如何提高喷嘴的能量传输效率。为此,在进行喷嘴设计时,一般从喷嘴的物理结构和射流流体性质两方面研究。通过理论分析计算,结合计算机仿真软件模拟,最后设计试验,对结果进行验证,并选择出能量传输效率最优的喷嘴。连续射流主要性能参数如下 [7] 。
2.1. 喷嘴流量
水射流喷嘴流量Q定义为射流速度u与喷嘴横截面积A乘积,即:
流量系数μ定义为喷嘴实际流量Q与理论流量
之比,即:
式中:
为喷嘴横截面积收缩系数;
为喷嘴速度系数。
2.2. 射流打击力
射流从喷嘴处获得了一定的速度和方向,由于靶物表面往往具有不同的形状,当射流对表面冲击时,其速度大小和方向会发生变化,射流的部分能量传递到靶物上,该部分能量以打击力的形式存在,并对靶物表面造成破坏。
由于在射流截面上各点速度不同,我们取一个假设的流体微元进行分析。流体微元在喷嘴出口处具有动量
,在冲击靶物表面之后,流体微元具有动量为
,则冲击靶物表面后损失的动量等于作用在靶物表面的作用力
。
式中:
为射流介质密度;
为流体微元所在位置的流量;
为流体微元速度。
由公式可得,当射流介质密度、流量、速度相同的情况下,流体微元速度方向与靶物表面夹角越大,打击力越大。当
时,打击力达到最大。随着喷射距离的变化,打击力也在变化。经过前人理论分析和大量的试验验证,对于圆柱形喷嘴形成的射流在喷嘴附近的打击力只有最大打击力的85%,随着喷射距离的增加,打击力也在变大,最大值所对应的靶距约为喷嘴直径的100倍,此后,随着喷射距离的继续增加,射流发散,速度降低,打击力逐渐减小。
2.3. 压力分布
圆柱形喷嘴连续射流以一定距离垂直冲击至靶物表面时,在不考虑重力的情况下,射流在靶物表面形成半径为 的圆形冲击区域,其中半径为R处位置定义为射流作用靶物表面压力等于环境压力。喷嘴轴线与靶物交点处为滞止压力
,在壁面上,随着与喷嘴轴线之间的距离 变大,打击力不断变小。因此,冲击区域内部各点压力P为:
冲击区域内打击力与半径满足一定关系,经展开成泰勒级数,可得到R与l的近似关系式:
对整个冲击区域积分,可得到冲击区域总打击力:
同时,射流垂直于靶物,总打击力又为:
式中:r为射流半径。
则冲击半径R与射流半径r关系为:
2.4. 喷嘴出口射流速度
式中:P为喷嘴入口压力。
2.5. 湍流强度
2.6. 扇形射流有效清洗宽度
扇形喷嘴不同于圆柱形喷嘴,扇形射流由于具有较大的喷射角,因此,其射流能量损失较大,卷吸有较多的空气,形成模糊的射流边界,无法清楚确定其有效的射流边界,另一方面,射流速度损失较大,无法达到清洗效果。基于此,我们采用实际有效清洗区域边界作为射流宽度。
待清洗物体表面污垢的成分千差万别,按照其理化性质,可分为硬质和软质污垢。硬质污垢多采用以渗透为主要的清洗方式,软质污垢多采用压缩和剪切为主的清洗方式。
扇形射流以一定速度作用于壁面上,在壁面上产生动压,通过测量扇形射流作用在壁面上产生的动压,与临界清洗压力比较,可得到扇形喷嘴实际有效清洗宽度范围。
3. 模型的建立与仿真
本文利用NX建立喷嘴的三维模型及外流域场,如图1所示。喷嘴的端面为水流入口(inlet),六面体的端面作为水射流打向的靶面,将建立好的模型导入到带有Fluent网格划分的功能的Fluent中进行网格划分,首先由于喷嘴相对于外流场尺寸较小,为了对扇形喷嘴的射流流场准确地仿真模拟,特对扇形喷嘴进行多面体网格划分,选择几何图形仅由没有空隙的流体区域组成,定义入口为压力入口,定义出口为压力出口。在Fluent中,选择基于压力、稳态、绝对速度的求解器类型,在操作环境中设置为一个标准的环境压力,选择z方向重力为9.81 m/s。由于喷嘴内外部流场中包含水和空气,采用VOF模型用于求解分层流。
在湍流模型中选择Realizable K-ε,从流体数据库中添加水相,并将空气作为第一相,水作为第二相,在相间作用中设置空气与水之间的表面张力系数为0.072 N/m,在全局选项中,选择表面张力模型,连续表面应力。
在边界条件中,喷嘴入口定义为压力入口,混合相总压为7.5 MPa,由于喷嘴入口直接与管道连接,设置喷嘴入口处全为水。命名为“outlet”的面设置为压力出口,其余面默认为“wall”。
在求解控制参数中,压力–速度关联形式选择SIMPLE算法,该算法在计算中可将亚松弛因子适当放大,提高了计算精度和稳定性,空间离散梯度选择Least Squares Cell Based,压力格式选择PRESTO!,动量方程、湍流动能、湍流耗散率均选择为First Order Upwind格式,初始化后,开始1000步迭代计算。
Figure 1. 3D model of a fan-shaped nozzle
图1. 扇形喷嘴的三维模型
4. 探究扇形喷嘴的影响因素
4.1. 探究V型切槽角对扇形喷嘴的影响
保持计算三维模型其他条件不变,改变图2中的扇形喷嘴V形切槽角度,研究V形切槽角度对射流参数的影响,分别建立了V形切槽半角为30˚、45˚、60˚的三种喷嘴三维模型。
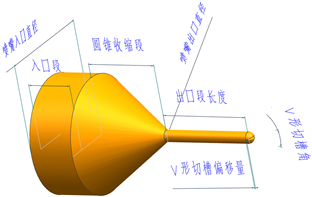
Figure 2. Influencing factors of sector nozzles
图2. 扇形喷嘴的影响因素
如图3,为三种喷嘴的内外部射流速度云图,V形切槽半角对外部射流速度影响较大。随着V形切槽半角减小,外部射流发散角增加,扩大了射流覆盖区域面积,但同时,较大的射流发散角会导致射流动能的损失。在图3(a)计算模型中,壁面上轴线附近,射流动能损失严重。在图3(c)计算模型中,射流集束性较好,射流动能损失也较小,但射流发散角较小,不合适用于清洗。
 (a)
(a)  (b)
(b)  (c)
(c)
Figure 3. Different V-shaped grooving angles, fan nozzle internal and external velocity clouds
图3. 不同V形切槽角度扇形喷嘴内外部速度云图
如图4,为三种扇形喷嘴轴线上射流速度分布情况,在喷嘴内部圆锥形收缩段,V形切槽角度越大的喷嘴,其射流加速性能越好,三组射流的最大速度相差不大,均与理论计算值接近。对于图3(a) 计算模型射流最大速度为123.020 m/s,到接近壁面X = −0.09 m时,速度为80.625 m/s,在此范围内,速度衰减了34.5%,图3(b)计算模型射流最大速度为124.288 m/s,到接近壁面X = −0.09 m时,速度为90.138 m/s,在此范围内,速度衰减了27.5%,图3(c)计算模型射流最大速度为126.226 m/s,到接近壁面X = −0.09 m时,速度为95.597 m/s,在此范围内,速度衰减了24.5%。在外部流场中,速度衰减速率与V形切槽角度成反比关系。
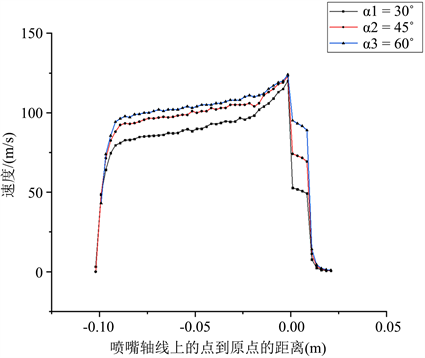
Figure 4. Speed distribution on the axis of the sector nozzle at different V-shaped grooving angles
图4. 不同V形切槽角度扇形喷嘴轴线上速度分布情况
4.2. 探究V形切槽偏移量对扇形喷嘴的影响
通过改变V形切槽偏移量,保持三维计算模型其他参数不变,建立了V形切槽偏移量为0 mm、0.1 mm、0.2 mm的三种计算模型。
如图5,为三种扇形喷嘴内外部射流的速度云图,随着V形切槽偏移量的增加,扇形喷嘴外部射流发散角逐渐减小,射流集束性能较好。对于图5(a)计算模型,壁面上沿径向原点附近,射流动能损失严重;对于图5(c)计算模型,作用于壁面上的动压较大,但射流发散角过小,不适合用于清洗。
 (a)
(a)  (b)
(b)  (c)
(c)
Figure 5. Different V-grooving offset sector nozzle internal and external velocity clouds
图5. 不同V形切槽偏移量扇形喷嘴内外部速度云图
如图6,为三种喷嘴轴线上射流速度分布情况,在外部流场,V形切槽偏移量越大,则轴线上射流速度衰减速率越小。对于图5(a)计算模型射流最大速度为125.183 m/s,到接近壁面X = −0.09 m时,速度为89.931 m/s,在此范围内,速度衰减了47.6%,图5(b)计算模型射流最大速度为124.356 m/s,到接近壁面X = −0.09 m时,速度为86.511 m/s,在此范围内,速度衰减了30.4%,图5(c)计算模型射流最大速度为123.423 m/s,到接近壁面X = −0.09 m时,速度为83.677 m/s,在此范围内,速度衰减了32.2%。
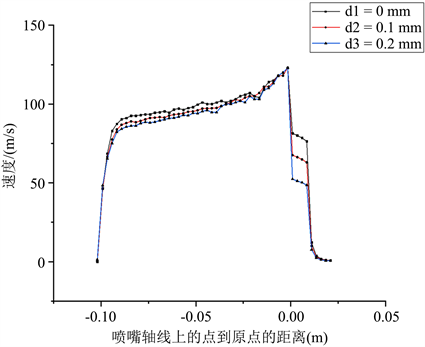
Figure 6. Velocity distribution on the axis of different V-shaped grooving offsets of sector nozzles
图6. 不同V形切槽偏移量扇形喷嘴轴线上速度分布情况
4.3. 探究出口段长径比对扇形喷嘴的影响
喷嘴出口长径比在2~4时,具有较好的射流性能,因此,本节中保持喷嘴其他参数不变,改变出口段长径比,分别建立了长径比为2、3、4的三种扇形喷嘴计算模型。
如图7,为三种扇形喷嘴内外部射流的速度云图,三种喷嘴形成的射流在具有相同发散角的同时,喷嘴出口段长径比越大,速度分布较为均匀。对于图7(a)和图7(b)计算模型,外部流场喷嘴轴线上的速度降低较快,而对于图7(c)计算模型,射流速度衰减速率较小,在壁面上,图7(c)计算模型射流速度分布也更为均匀。
 (a)
(a)  (b)
(b)  (c)
(c)
Figure 7. Inside and outside velocity clouds of sector nozzles with different outlet section length-to-diameter ratios
图7. 不同出口段长径比扇形喷嘴内外部速度云图
如图8,为三种喷嘴轴线上射流速度分布情况,在外部流场,V形切槽偏移量越大,则轴线上射流速度衰减速率越小。对于图7(a)计算模型射流最大速度为126.509 m/s,到接近壁面X = −0.09 m时,速度为94.066 m/s,在此范围内,速度衰减了25.6%,图7(b)计算模型射流最大速度为126.226 m/s,到接近壁面X = −0.09 m时,速度为95.479 m/s,在此范围内,速度衰减了24.4%,图7(c)计算模型射流最大速度为125.290 m/s,到接近壁面X = −0.09 m时,速度为94.065 m/s,在此范围内,速度衰减了24.9%。
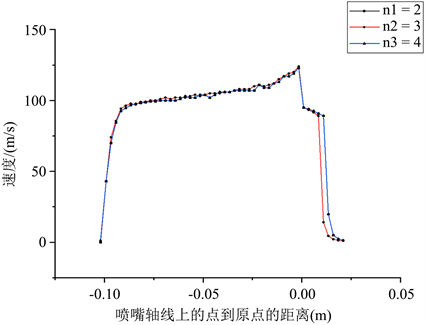
Figure 8. Speed distribution on the axis of sector-shaped nozzles with length-to-diameter ratios of different outlet sections
图8. 不同出口段长径比扇形喷嘴轴线上速度分布情况
4.4. 探究入口压力对扇形喷嘴的影响
本节中计算模型保持其他条件不变,通过改变扇形喷嘴入口压力,研究入口压力对射流性能的影响。
如图9,为该扇形喷嘴在三种不同入口压力下形成的射流速度云图,喷嘴入口压力增大,射流发散角略有变大,三种喷嘴仿真结果中射流最大速度依次为112.828 m/s、121.206 m/s、129.040 m/s,根据公式可得三种压力下,射流理论最大速度依次为113.963 m/s、122.416 m/s、130.322 m/s,三种喷嘴射流速度的误差为0.1%、0.1%、0.1%,该误差值在可接受范围内。同时,喷嘴入口压力增大,导致外流场中各点射流速度均有所增加。
 (a)
(a)  (b)
(b)  (c)
(c)
Figure 9. Different inlet pressure fan nozzle internal and external velocity clouds
图9. 不同入口压力扇形喷嘴内外部速度云图
如图10,为三种喷嘴轴线上射流速度分布情况,在外部流场,V形切槽偏移量越大,则轴线上射流速度衰减速率越小。对于图9(a)计算模型射流最大速度为112.828 m/s,到接近壁面X = −0.09 m时,速度为64.35 m/s,在此范围内,速度衰减了42.9%,图9(b)计算模型射流最大速度为121.206 m/s,到接近壁面X = −0.09 m时,速度为87.73 m/s,在此范围内,速度衰减了27.6%,图9(c)计算模型射流最大速度为129.040 m/s,到接近壁面X = −0.09 m时,速度为93.42 m/s,在此范围内,速度衰减了27.6%。从以上数据结论可得,在此计算情况下,喷嘴入口压力与射流速度成正比关系,喷嘴轴线上射流速度减小越慢,表明射流动能损失越少。
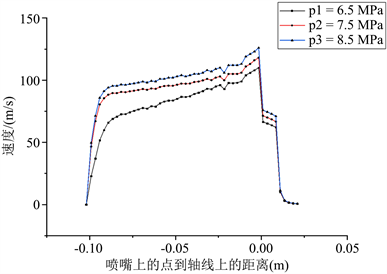
Figure 10. Speed distribution on the axis of different inlet pressure fan nozzles
图10. 不同入口压力扇形喷嘴轴线上速度分布情况
5. 喷嘴结构参数优化设计
为了反映出各个结构参数对扇形喷嘴的射流性能的影响,采用正交试验设计,如表1所示用A表示V型切槽角的变化,B表示V形切槽偏移量的变化,C表示出口段长径比的变化和D表示入口压力的变化等4个因素,从实物喷嘴的量级范围内对这4个因素分别选取3个水平。
试验中挑选出部分有代表性的点进行试验,使试验点在试验范围内均匀分散,能反映出全面的情况。文中试验是四因素三水平正交试验,根据正交试验表设计出试验组数。

Table 2. Number of experimental groups
表2. 实验组数
对于正交试验中四个目标的优化问题,常采用综合评价法和综合平衡法来处理数据。
1) 综合评价法。该方法的原理是将不同的优化目标转换成一个优化目标,常采用加权平均法进行转换。由于不同优化目标在优化问题中的重要性不同,因此,需提前计算出各优化目标所占权重比,最后通过公式计算得到各组实验结果。
2) 综合平衡法。该方法的原理是分别对各个优化目标进行处理,通过对各个优化目标的优化结果进行综合评价。由于本节中四个优化目标之间重要性相同,且权重比无法计算,因此,采用综合平衡法对优化问题进行分析。
实验结果分析:
按照表2中因素顺序,根据上一章所述的对扇形喷嘴内外流场仿真方法,对表3中的扇形喷嘴模型开展流场仿真分析,表3为计算结果。
对于流量来说,应满足水泵所能提供的流量大小。各因素对流量的影响程度由大到小分别为V形切槽偏移量B > V形切槽半角A > 入口压力D > 喷嘴出口段长径比C。流量随着V形切槽半角和入口压力的增加而增加,随V形切槽偏移量的增加而减小,喷嘴出口长径比对流量影响可忽略不计,A、B、D三个因素还需根据其他优化目标继续进行分析。
对于打击力来说,各因素对打击力的影响由大到小分别为入口压力D > V形切槽偏移量B > V形切槽半角A > 喷嘴出口段长径比C。打击力随着V形切槽半角和入口压力的增加而增加,随V形切槽偏移量的增加而减小,喷嘴出口长径比对流量影响可忽略不计。
各因素对有效清洗宽度的影响由大到小分别为V形切槽偏移量B > 喷嘴出口段长径比C > 入口压力D > V形切槽半角A。射流作用于壁面上的有效清洗宽度随着V形切槽半角的增加而增加,当V形切槽偏移量为0.3 mm时,具有最大有效清洗宽度,为75 mm,喷嘴出口段长径比可选择在3~4之间,入口压力可选择为7.5 MPa。
6. 结论
本文研究以清扫车的清洗系统为研究对象,基于流体力学的理论知识,采用Fluent数值仿真和实验的方法相结合,利用NX软件结合清洗系统的参数对清洗系统中的扇形喷嘴进行三维建模。利用Fluent软件对洗扫车清洗系统中的扇形喷嘴进行模拟仿真分析,再用正交试验法进行多目标优化设计,研究了某型号扇形喷嘴的结构参数的变化对其射流性能的影响,提出了一套系统研究扇形喷嘴的结构参数优化的分析设计方法。通过模拟实验数据综合分析,得到以下结论:对于该类型的扇形喷嘴,V形切槽半角应选取45˚,V形切槽偏移量0 mm,出口长径比为4,入口压力为7.5 MPa。
基金项目
盐城工学院校级科研项目资助(项目编号:xjr2023001)。