基于GA优化的纯电动汽车能量管理策略研究

Research on Energy Management Strategy of Pure Electric Vehicle Based on GA Optimization

摘要: 为了解决单纯使用经验得到的隶属度函数构建的模糊控制器无法使纯电动汽车的电能控制效率最大化这一问题，提出了一种基于遗传算法优化的模糊PID控制策略。首先，在AVL Cruise软件中搭建纯电动汽车整车模型，同时根据整车能量管理策略设计了模糊PID控制器。在此基础上，采用遗传算法进一步优化模糊PID控制器的隶属度函数并建立能量管理策略模型，通过MATLAB/Simulink和AVL Cruise软件进行联合仿真。结果表明，所提遗传算法优化的模糊PID控制策略提高了整车的能量利用率，能够有效改善蓄电池的放电状态，延长电池的使用寿命，在NEDC循环工况下，最大爬坡度提高了18.71%，整车百公里加速时间缩短了15.25%，百公里耗电量降低了13.78%，有效提高了整车的动力性和经济性。所设计的能量管理策略为新能源汽车发展提供参考。

Abstract: In order to solve the problem that fuzzy controllers constructed solely using membership functions obtained from experience cannot maximize the efficiency of electric vehicle energy control, a fuzzy PID control strategy based on genetic algorithm optimization is proposed. Firstly, a pure electric vehicle model was built in AVL Cruise software, and a fuzzy PID controller was designed based on the vehicle energy management strategy. On this basis, genetic algorithm is used to further opti-mize the membership function of the fuzzy PID controller and establish an energy management strategy model. Joint simulation is conducted using MATLAB/Simulink and AVL Cruise software. The results show that the proposed genetic algorithm optimized fuzzy PID control strategy achieves the best energy utilization of the entire vehicle, effectively improving the discharge state of the battery, prolonging the service life of the battery. Under NEDC cycle conditions, the maximum climbing slope is increased by 18.71%, the acceleration time per 100 kilometers is shortened by 15.25%, and the power consumption per 100 kilometers is reduced by 13.78%, effectively improv-ing the power and economy of the entire vehicle. The designed energy management strategy pro-vides a reference for the development of new energy vehicles.

1. 引言

近年来，清洁高效的新能源汽车是现代汽车工业首要发展的主题，所以各国政府均开始大力发展纯电动车 [1] 。锂电池绿色环保且具备高功率承受力，但是鉴于其能量密度接近其理论上限，则有限电池能量难以提升续航里程 [2] 。

纯电动汽车的能量管理优化主要靠采取控制策略后，能量管理系统使能量在转换装置之间按照最优路径流动，使得能量利用率达到最高 [3] ，进而提升整车的动力性和经济性。相关研究人员针对这一关键技术进行了实验分析：王琦 [4] 等基于Cruise与Simulink搭建了纯电动汽车联合仿真平台，设计了模糊控制能量管理策略，仿真结果表明整车有较好的动力性和经济性；郝美超 [5] 等基于MATLAB/Simulink环境采用模糊神经网络控制电源系统的功率分配策略，提高了纯电动汽车的动力性和能量利用率；Lu Y [6] 等设计了模糊控制的能量管理策略，基于Cruise与Simulink联合仿真并验证了该策略对动力电池具有良好的优化效果；田丽媛 [7] 等提出了一种基于动态规划算法的纯电动汽车能量管理优化方法，有效减少了动力电池的消耗量。

上述研究的方法若在使用之前优化改进，对纯电动汽车的能量管理效果会更显著。所以本文在控制策略的基础上将遗传算法应用于纯电动汽车能量管理模糊PID控制器设计中，优化模糊PID控制器的隶属度函数，通过MATLAB/Simulink和AVL Cruise软件联合仿真，结果表明基于遗传算法优化的模糊PID控制策略使纯电动汽车具有更好的动力性和经济性。

2. 理论分析与模型建立

2.1. 纯电动汽车的动力系统结构及分析

纯电动汽车的动力系统结构主要由动力电池，电机控制器和驱动电机等组成 [8] ，其结构如图1所示。其中动力电池组是决定续航里程的关键部件；驱动电机的作用是驱动车轮转动使整车行驶；电机控制器的作用是保护电池防止过放电；DC/DC变换器是一种将动力电池组输出的高压电转换为低压电的电源转换装置。

Figure 1. Diagram of power system structure of pure electric vehicle

图1. 纯电动汽车动力系统结构图

由上图可以看出动力系统之间输入输出的能量关系，在车辆行驶过程中能量关系可以表示为：

$Q_L=Q_e-\left(Q_m+Q_a+Q_o\right)$ (1)

式中： $Q_L$ 为整车剩余能量； $Q_e$ 为电池总能量； $Q_m$ 为驱动行驶能耗； $Q_a$ 为辅助系统能耗； $Q_o$ 为其他设备能耗。

利用整车的能量管理，并对驾驶员的需求总能进行分析，优化能量管理策略，实现整车的能量消耗降低，达到优化整车经济性的目的。

在驱动电机中，在旋转磁场与转子电流的相互作用下产生了电机的电磁转矩 [9] 。由于转子电流以及旋转磁场每个电极的磁通与电磁转矩T的幅值成正比，可以进一步地推导出电磁转矩与电压的关系式：

$T=K{U}_1^2\frac{s{R}_2}{R_2^2+{\left(s{X}_{20}\right)}^2}$ (2)

式中：T表示电磁转矩；K为常数； $U_1$ 为定子绕组相电压的有效值；s表示转差率； $R_2$ 表示转子每相绕组的电阻； $X_{20}$ 为转子静止时转子电路漏磁感抗。

通过(2)式可看出驱动电机中转矩与电压的平方成正比，通过更合理有效的能量管理策略，可使车辆在行驶过程中具有更稳定的转矩和充足的动力，达到优化整车动力性的目的。

2.2. 纯电动汽车的整车建模

本文以某纯电动汽车为研究对象，利用AVL Cruise软件搭建整车模型。整车的主要性能参数和动力经济性指标如表1所示。

纯电动汽车的整车模型如图2所示，在AVL Cruise软件的组件库中将各个组件模块拖到建模窗口并进行连接(红色连线为电气连接，蓝色连线为机械连接)，根据整车参数在各个组件模块中输入相应的数据，则完成纯电动汽车的整车建模。

Table 1. Whole vehicle parameters and indicators of pure electric vehicles

表1. 纯电动汽车整车参数及指标

Figure 2. Vehicle model

图2. 整车模型

3. 模糊PID控制器的设计与优化

3.1. 模糊PID控制系统设计

模糊PID控制器中，模糊控制器的主要作用是实时在线调整PID参数，其控制框图如图3所示。

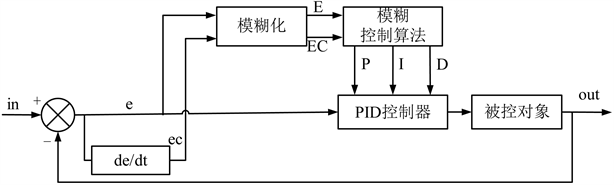
Figure 3. Fuzzy PID control block diagram

图3. 模糊PID控制框图

设计模糊PID控制器的主要步骤为：

(1) e为选择偏差、ec为偏差变化，输出的模糊语言变量为E、EC和 $K_p$ ， $K_i$ ， $K_d$ 。根据E、EC和PID参数实际的基本论域，将E、EC设定为[−3, 3]， $K_p$ 为[−0.4, 0.4]， $K_i$ 为[−0.06, 0.06]， $K_d$ 为[−3, 3]。模糊控制器前后的GAIN模块为比例因子，可将输出转换到论域范围。

(2) 选取E、EC和PID参数的各语言变量值：PB为正大，PM为正中，PS为正小，Z0为零，NS为负小，NM为负中，NB为负大。论域上的模糊子集隶属度函数，在输入和输出中采用三角形和高斯形。

(3) 选择一种模糊判决方法，即建立控制规则，将控制量由模糊量变为精确量 [10] 。模糊控制规则的静态特性有：完备性，相容性和干涉性。规则形式如下：

if E = NB, EC = NM, then $K_p$ = PB

模糊PID控制规则表如表2所示。

Table 2. Fuzzy PID control rules

表2. 模糊PID控制规则

模糊PID控制器具有稳定、可靠和适应强等优点，将模糊规则运用到PID控制器中可加强其鲁棒性，如图4所示，基于MATLAB/Simulink环境下将模糊PID控制和PID控制进行仿真对比。

由图4可看出模糊PID控制器有较好的效果，具有响应时间快速，消除稳态偏差的优点，但仍然具有超调量，采用经验法选取模糊规则具有一定的局限性，还有改进的空间。将遗传算法与模糊PID控制相结合，对模糊规则及其参数进行全局寻优，使模糊控制规则不受人为经验的限制，进一步优化模糊PID控制器。

3.2. 基于GA的模糊PID控制器参数优化

遗传算法(Genetic Algorithm)简称GA，是一种通过模拟自然进化过程的随机全局搜索优化方法 [11] ，它模拟了自然选择和遗传过程中发生的复制、交叉和变异等现象，从任意初始种群出发，经过随机选择，产生一群更适应环境的个体，再经过交叉和变异等操作，使其进化到搜索空间中越来越好的区域。经过一代又一代不断地繁衍和进化，最后，它会收敛到一群最能适应环境的个体中，从而获得最好的解决方案，其基本流程如图5所示。近年来遗传算法已经在混合设计、机器学习、信号处理以及自适应控制等多个方面取得了成功广泛的应用，成为一个寻找全局最优解的快速优选方法。所以，可以通过遗传算法来对控制规则及参数进行优化调整

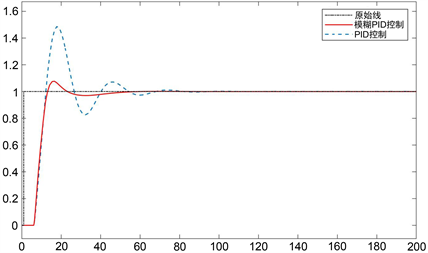
Figure 4. Simulation comparison between fuzzy PID control method and PID control method

图4. 模糊PID控制法与PID控制法仿真对比图

Figure 5. Genetic algorithm flowchart

图5. 遗传算法流程图

3.2.1. 编码及种群初始化

编码即将可行解的空间转化为染色体的搜索空间。待优化的元素共有147个，鉴于二进制编码具有较强的搜索能力，且控制规则变量较多，则采用二进制整数编码，有利于提高算法速度。在遗传算法程序中用整数7、6、5、4、3、2、1分别代替控制表中的PB、PM、PS、Z0、NS、NM、NB模糊子集。初始化的种群是先随机产生一定数目的个体，然后从中挑选最好的个体加入到初始化种群，此过程不断迭代，种群始终维持在100的相同规模。

3.2.2. 适应度函数的选取

为避免遗传算法优选的功能被弱化，适应度函数通过标定目标函数来确定，其中目标函数由ITAE性能指标进行转化 [12] ，进而优化目标函数的最大值。公式如下所示。

$\{\begin{array}{l}F\left(x\right)=a\cdot f\left(x\right)+b\\ b=a\cdot \left(-f_{\min }\left(x\right)+\epsilon \right)\\ J={\displaystyle {\int }_1^{\infty }t\Vert e\left(t\right)\Vert \text{d}t}\\ f\left(x\right)=\frac{1}{1+J\left(x\right)}\end{array}$ (3)

式中， $F\left(x\right)$ 为适值函数； $f\left(x\right)$ 为目标函数； $f_{\min }\left(x\right)$ 为目标函数的最小值；x为染色体；a，b为系数；J为性能指标； $e\left(t\right)$ 为系统误差； $\epsilon$ 为染色体被选中迭代的概率。

3.2.3. 遗传操作

选择操作是确定从亲代种群中依据适应度值优胜劣汰的方式选取某些个体，将其基因遗传到下一代种群中的一种遗传运算。本文设定的选择概率为0.9。

交配重组在遗传过程中是生物进化的一个重要环节 [13] ，在遗传算法中起着关键作用为交叉运算，采用随机配对，将种群中的每个个体以随机的方式完成配对，交叉操作则在这些配对个体中进行。交叉概率越大，各代的交叉就越充分，但其中的优良个体可能会遭到破坏。本文设定的交叉概率为0.9。

变异是对遗传过程的改进，当变异概率较小时，解的稳定性较高，但因此会使其很容易陷入局部最优解 [14] ；为更好地找到全局最优解，将变异概率增大，解空间可更具有多样性。本文设定的变异概率为0.1。

2.2.4. 终止条件

遗传算法不仅可以通过最大迭代次数来判断程序运行是否终止，若种群达到最大迭代次数之前就完成收敛，也应结束迭代，即也可以用适应度函数来判断终止条件 [15] 。本文的遗传算法程序是当迭代次数达到100次时就自动停止，最优解 $F\left(x\right)=0.\text{5336}$ 。适应度曲线如图6所示。

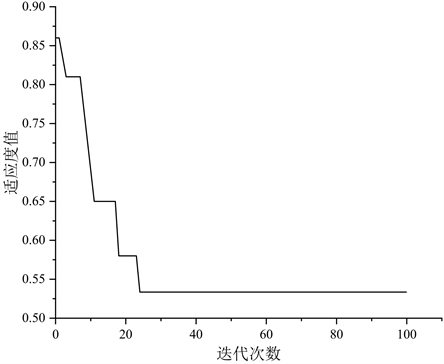
Figure 6. Change curve of fitness value

图6. 适应度值变化曲线

3.3. 优化结果

根据纯电动汽车能量管理系统的实际情况，取其输入输出量的论域为E = EC = [−3, 3]，K_p为[−0.4, 0.4]，K_i为[−0.06, 0.06]，K_d为[−3, 3]，结合以上数据：选取样本个数为100，选择概率与交叉概率均为0.9，变异概率为0.1。优化后的隶属度函数与优化后的仿真效果如下图7所示。

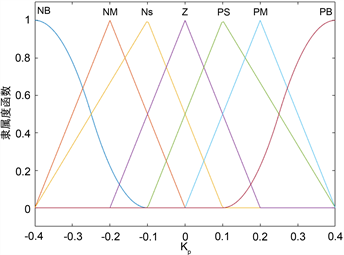(a) 优化后K_p的隶属度 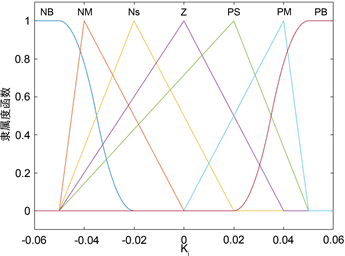(b) 优化后K_i的隶属度 (c) 优化后K_d的隶属度 (d) 优化后的仿真对比

Figure 7. Comparison between the optimized output membership function and simulation

图7. 优化后输出的隶属度函数图与仿真对比

通过优化过后的模糊PID控制器模拟仿真可以看出，遗传算法的优化使其不仅具有响应时间快速，消除稳态偏差的优点，并且调整了超调量，加强了运行中的稳态。至此，由遗传算法优化后的模糊PID控制器的可行性与优越性得到初步验证。

4. 仿真结果及分析

为了验证遗传算法对纯电动汽车能量管理策略改进的有效性及优越性，根据以上方法利用MATLAB/Simulink联合AVL Cruise进行仿真，模型如图8所示。

基于图2的整车模型，将其与经过遗传算法优化后的模糊PID控制策略模型结合，将图8中的控制策略模型编译成DLL文件放入图2中的CruiseMatlabDLL模块中，通过端口连接传递控制信息。针对纯电动汽车的动力性及经济性，通过整车的百公里加速时间，最大爬坡度和百公里耗电量等比较，来说明遗传算法优化模糊PID控制器的优越性。

Figure 8. Fuzzy PID control strategy model

图8. 模糊PID控制策略模型

4.1. 动力性仿真与分析

汽车动力性最直观的体现就是百公里加速时间，加速所用的时间越短，汽车加速性能越好，即整车的动力性就越好。由图9可看出，优化前的纯电动汽车百公里加速时间为10.29 s，而优化后加速时间明显缩短至8.72 s。整车动力性有很大的提升。

Figure 9. Acceleration time of 100 kilometers

图9. 百公里加速时间

整车动力性的另一重要评定指标——最大爬坡度，即汽车在满载或一定载荷下的爬坡能力；其能克服的最大坡度越大，说明爬坡能力越强，即动力性越好。本文是在满载情况下仿真的最大爬坡度，其优化前后比对效果如图10所示。

由图10可看出优化前的爬坡度为30.69%，优化后为36.44%，最大爬坡度有很大的提升。对于整车动力性来说，在采用了遗传算法优化过后的模糊PID控制器之后，百公里加速时间缩短了15.25%，最大爬坡度提升了18.71%。动力性仿真结果对比如表3所示。

4.2. 经济性仿真分析

纯电动汽车的经济性指标主要指能够用最少的电力消耗量完成单位运输工作的能力，则采用百公里行驶的电力能耗为评定指标。

Figure 10. Maximum climbing slope

图10. 最大爬坡度

Table 3. Comparison of power performance simulation results

表3. 动力性仿真结果对比

如图11所示为NEDC循环工况下计算的纯电动汽车的百公里耗电量，从优化前和优化后的SOC变化情况，可明显地看出使用遗传算法优化的模糊PID控制的SOC下降趋势更缓慢，在相同的工况下，锂电池的能耗相对优化前更为平缓，可以延长锂电池的使用寿命。

Figure 11. SOC values before and after optimization

图11. 优化前后的SOC值

经过遗传算法优化后的能量管理模糊PID控制能更准确地对驾驶员的需求总能进行分析，避免了过多的功率流失，可见优化过后可使动力电池能够在良好的环境下工作，从而使整车经济性得到提升。如图12所示。

Figure 12. Power loss values before and after optimization

图12. 优化前后的功率损耗值

通过AVL Cruise 对纯电动汽车的经济性仿真中，优化前的百公里电耗为13.64 kWh/100km，优化后的百公里电耗为11.76 kWh/100km，优化效率为13.78%，如表4所示。随着功率损耗的降低，可以减少电池的充放电次数，延长电池的工作寿命。

Table 4. Comparison of simulation results of power consumption per 100 kilometers

表4. 百公里电耗仿真结果对比

5. 结语

针对纯电动汽车的能量管理，本文提出了一种基于遗传算法优化的模糊PID控制策略，充分利用整车的电能，提高整车的动力性能和经济性能。研究结论如下：

1) 设计了模糊PID控制器，并采用遗传算法优化其隶属度函数。仿真结果表明，遗传算法优化后，其响应时间更快速，消除稳态偏差，有效加强运行中的稳态。

2) 基于纯电动汽车整车模型，分析了动力系统与能耗的关系，提出了能量管理控制策略。仿真结果表明，优化后整车的百公里加速时间缩短了15.25%，最大爬坡度提高了18.71%，提升了整车的动力性能；百公里电耗降低了13.78%，锂电池的SOC值下降更缓慢，延长使用寿命，提升了整车的经济性能。

本文将遗传算法应用在模糊PID控制中，可显著提高纯电动汽车的能量利用率，但不足之处是未进行实验验证，有待以后进一步的研究，同时可结合再生制动能量回收策略，提高电动汽车的续航里程。

基金项目

贵州省科技支撑计划(黔科合支撑[2023]一般400)。

NOTES

^*第一作者。

^#通讯作者。