1. 引言
在金属挤压加工领域,挤压筒是必不可少的加工工具,其中扁挤压筒因其内孔与扁宽薄壁的型材有着相似的几何形状,使得金属流动性更加均匀,能有效提高成品质量和降低模具损耗程度。在相同的挤压能力下,扁挤压筒比圆挤压筒能挤出更大宽度的壁板型材,在挤压生产扁宽薄壁板型材中有着极大的优势 [1] [2] 。
由于扁挤压筒内孔的自身结构,其圆弧过渡处容易出现应力集中的现象 [3] 。因此扁挤压筒设计一般采用多层结构,通过各层之间的过盈配合产生预紧力,可抵消挤压生产时产生的部分拉应力,起到改善圆弧过渡处应力集中现象的作用,并且容易更换因摩擦而产生损伤的内层,同时在经济性和结构紧凑性等方面优于单层筒 [4] [5] [6] 。ALEGRE等 [7] 提出了一种高压容器缠绕仿真分析方法,并通过实验对分析结果进行了验证。因钢丝本身具有很高的强度,通过在挤压筒上缠绕一定的钢丝层数,可以为挤压筒提供巨大的预紧力,使得挤压筒处于均匀的压应力保护状态中 [8] [9] 。吴任东等 [10] 采用有限元方法,分析了预应力钢丝缠绕圆挤压筒的受力分布及特点,论证了预应力钢丝缠绕圆挤压筒结构的可行性和优势。另外,预应力钢丝缠绕结构在75℃温度下,其蠕变和应力松弛影响较小,能保持稳定的预紧应力 [11] 。
因此本文根据扁挤压筒结构形状对其内层进行剖分,同时采用钢丝对剖分后的扁挤压筒进行缠绕,并采用有限元方法对钢丝缠绕的整体式和剖分式扁挤压筒应力进行研究分析。
2. 钢丝缠绕剖分式扁挤压筒结构
2.1. 结构原理
图1所示为钢丝缠绕剖分式扁挤压筒结构剖视图,由内层、中层、外层和钢丝层组成,图中A为扁挤压筒长轴,B为扁挤压筒短轴,在外层外表面设有环形凹槽,且槽内用钢丝缠绕形成预应力钢丝层,从而使内层处于压应力保护状态,在挤压成型时能够抵消内壁压力而产生的拉应力,进而提高内层挤压筒的抗挤压能力。另外,通过缠绕钢丝的方式对挤压筒施加预应力,可以避免多层挤压筒过盈配合时的装配困难问题。考虑到内层在挤压状态下会承受极大的拉应力作用,特别是两端圆弧是扁挤压筒容易失效和产生疲劳破坏的部分,因此根据未裂先分原理对扁挤压筒的内层沿长轴方向进行剖分,从而改善扁挤压筒内层的受力状态,进而改善内层在工作状态下因内压而产生的恶劣环境,同时还能降低扁挤压筒内壁切削加工的难度。
2.2. 有限元模型
在ANSYS有限元软件中,筒体使用具有超弹性,蠕变,大变形和大应变能力的实体单元进行建模,

Figure 1. Section view of steel wire winding split flat extrusion cylinder structure
图1. 钢丝缠绕剖分式扁挤压筒结构剖视图
为了降低计算成本,钢丝使用BEAM189梁单元进行建模,该单元是基于Timoshenko梁理论,其中包含剪切变形效果。非常适合线性、大旋转和/或大应变非线性应用,能分析弯曲、横向和扭转稳定性问题,支持弹性、塑性、蠕变等非线性材料模型。同时采用降温法模拟钢丝收缩时产生的拉应力来实现钢丝预应力的施加,这样钢丝预应力的施加就转化为温度载荷的施加,其应力公式如下:
式中:
为温度差;
为钢丝预加力;
为钢丝弹性模量;
为钢丝横截面积;
为钢丝膨胀系数;
为钢丝预应力。
钢丝缠绕方式一般分为等切应力缠绕、等剪应力缠绕和等张力缠绕 [12] 。本文采用等张力缠绕方式对整体式和剖分式的扁挤压筒分别施加了10层,每层为150 MPa的预应力,内壁所施加的内压均为380 MPa并进行有限元分析。扁挤压筒长、短轴尺寸
,内层外半径
,中层外半径
,外层外半径
,筒高
,为便于计算,本文将设计尺寸进行等比例缩小后建模计算并不考虑过盈量对扁挤压筒的影响。扁挤压筒的材料采用4Cr5MoSiV1热作模具钢,抗拉强度1725 MPa,弹性模量为2.1E5 MPa,泊松比为0.3。根据扁挤压筒结构取1/8模型,如图2所示。在模型的对称面上施加对称约束,而对剖分式扁挤压筒内层的剖分面D则采用受压不受拉约束。
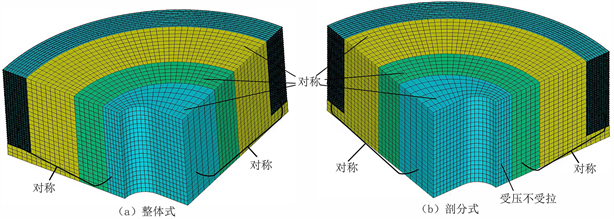
Figure 2. Finite element model of steel wire wound flat extrusion cylinder
图2. 钢丝缠绕扁挤压筒有限元模型
3. 计算结果与讨论
由参考文献 [3] 理论计算结果结合仿真显示,扁挤压筒在工作时,筒壁的受力并不均匀,内壁的受力最大,而应力的大小在扁挤压筒上的分布由内向外逐渐减小,内壁会由于过大的应力过早的破坏。因此对于扁挤压筒,内层是容易损坏的部位,内层的受力情况决定着扁挤压筒的使用寿命和承载能力,在扁挤压筒的设计过程中,研究内层的应力分布极为重要。整体式扁挤压筒的内层内壁是非常容易失效的区域,其应力分布和变化趋势能有效反映内层挤压筒的危险区域,另外对内层结构的改进提供了直观的依据。
3.1. 第一主应力分布
如图3所示,通过有限元方法对整体式和剖分式的预应力钢丝缠绕扁挤压筒进行分析,发现整体式内层内壁圆弧处的第一主应力明显大于其他部分,且壁厚越小第一主应力越大(约761 MPa),而剖分式的扁挤压筒内层第一主应力分布变得较为均匀,内壁处的第一主应力峰值得到明显的降低(约188 MPa)。这是由于整体式内层受到较大的拉应力,而剖分式扁挤压筒由于结构的不连续性,使得剖分面处的拉应力显著降低,从而使其第一主应力的峰值降低。根据第一强度理论即最大拉应力理论,降低内层第一主应力的峰值能有效减小材料发生断裂的风险,在相同挤压力情况下,剖分式挤压筒内层疲劳破坏风险降低,能有效提高挤压筒寿命。
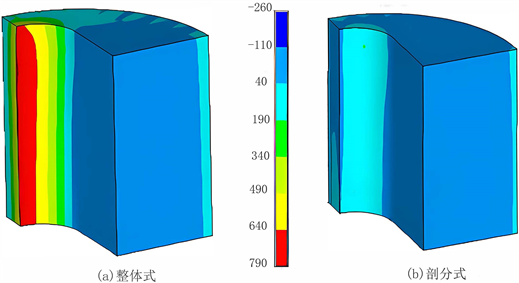
Figure 3. The first primary stress cloud diagram of the inner layer
图3. 内层第一主应力云图
3.2. 最大切应力分布
在分析了整体式和剖分式的内层第一主应力分布后,进一步对内壁最大切应力的分布进行研究。分别选取整体式和剖分式的扁挤压筒内层内壁的所有节点,得到受力状态下各节点的应力数值,根据第三强度理论得到其最大切应力公式:
式中:
为最大切应力,
为第一主应力,
为第三主应力。
计算各节点最大切应力数值并绘制其内壁最大切应力分布图,如图4所示,无论是整体式还是剖分式扁挤压筒,在轴向上应力分布比较均匀,这是由于挤压筒在轴向上的长度较大,可以认为是平面应变问题。在内层为整体式的情况下随着X轴坐标的增大,切应力逐渐增大,在内层壁厚最小处,最大切应力数值达到最大(约558 MPa),这是因为在此处挤压筒内壁为圆弧结构,挤压筒在受到挤压力的同时还受到弯曲力作用。而得益于内层剖分的设计结构,剖分后的内层内壁切应力峰值得到显著的降低,最大值出现在圆弧段中间处(约280 MPa),壁厚最小处的切应力集中现象得到了改善,根据第三强度理论,剖分式的挤压筒的抗挤压能力能够得到提高。
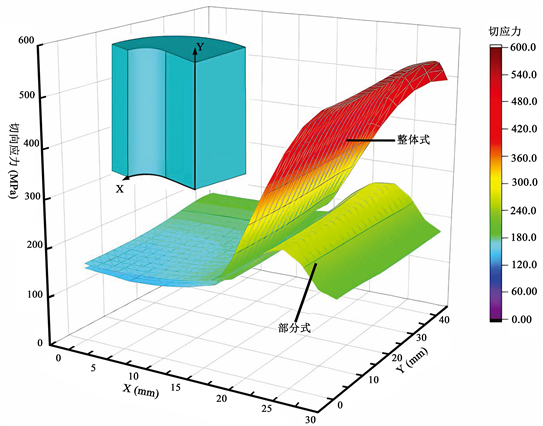
Figure 4. Maximum shear stress distribution of the inner wall
图4. 内壁最大切应力分布
3.3. 内壁周向应力分布
如图5所示,在直线mo段的法向应力(图5(a)),整体式和剖分式内层所有压应力比较接近,并从m到o逐渐减小,在圆弧段整体式和剖分式挤压筒所受压应力差别较大。剖分式挤压筒内层的压应力在整体上要大于整体式挤压筒内层的压应力,内层剖分式的设计结构在有效降低内壁周向拉应力的同时增加了径向压应力,这是因为剖分后,挤压筒的受压状态发生了改变,切应力降低第三主应力增大。沿mon路径取各节点沿内壁轮廓方向分布的应力数值并绘制成图。在直线mo段的切向应力(图5(b)),整体式与剖分式应力数值都相差不大且都表现为受压应力状态,而在圆弧on段的切向应力,整体式呈现逐渐增大的趋势且在内层壁厚最小处(圆弧on段末尾)出现应力峰值(约761 MPa);剖分式切向应力则明显低于整体式切向应力,且在内层壁厚最小处出现的应力峰值现象也得到了改善,这种现象是基于根据侧向支撑原理和未裂先分原理,即剖分后的挤压筒在周向上不连续,这种结构能减少内压产生的切向应力,由于扁挤压筒被剖分成块后,每个剖分块都是独立的结构,对扁挤压筒施加高压载荷后,剖分块在高内压的作用下,产生相互分离的趋势,这种相互分离的趋势是剖分式挤压筒内壁切向应力变小的主要原因。切向应力最大值出现在圆弧中间处(约162 MPa),因为此处受到了附加的弯曲力作用。
4. 结论
1) 在扁挤压筒的设计中,提出了钢丝缠绕剖分式扁挤压筒的结构,降低了扁挤压筒的制造装配难度,同时建立了相应有限元模型。
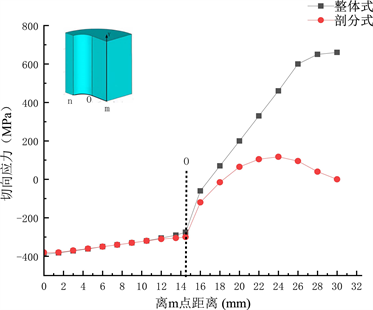
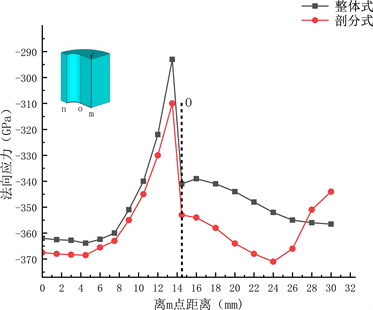 (a) 法相应力 (b) 切向应力
(a) 法相应力 (b) 切向应力
Figure 5. The circumferential stress distribution of the inner wall
图5. 内壁周向应力分布
2) 扁挤压筒经过剖分后,其内层应力得到了显著降低。内层内壁圆弧处作为扁挤压筒最容易失效的区域,剖分式内层有效降低了内层内壁的最大切应力峰值,同时消除了圆弧处的应力集中现象,提高了内层的抗疲劳破坏和承载能力。
3) 扁挤压筒内壁在轴向上应力分布比较均匀,在圆周方向分布不均匀。与内层整体式相比,内层剖分式由于结构的不连续性,使得剖分面处的拉应力显著降低,其内壁应力沿周向分布更加均匀。
致谢
本文作者非常感谢大学生创新创业训练计划项目,同时感谢团队其他成员的协助,他们的支持和协助使得大创项目能够顺利进行。
基金项目
大学生创新创业训练计划项目(项目编号:S202210361094)。