基于Wavenet的燃煤锅炉NOx排放浓度预测模型

NOx Emission Concentration Prediction Model for Coal-Fired Boilers Based on Wavenet

摘要: 基于数据驱动的方法对国内西北地区某火电厂660 MW燃煤机组的SCR脱硝入口NOx浓度建立预测模型。首先对火电厂DCS系统采集的数据进行数据预处理，包括开机判定、LOF算法异常值筛除，然后采用随机森林进行特征选择，最后分别采用Wavenet (波网)、LSTM (长短期记忆网络)、SVR (支持向量回归)三种方法分别对SCR脱硝入口NOx排放浓度进行预测。结果表明：无论是预测时间还是各项评价指标，Wavenet都表现更为优秀，其预测结果的平均百分比误差(Mean Absolute Percentage Error, MAPE)仅为1.31%，r2决定系数达到了0.97，充分显示Wavenet有比较好的预测能力。

Abstract: Based on the data-driven method, a prediction model was established for the NOx concentration at the SCR denitrification inlet of a 660MW coal-fired unit of a thermal power plant in northwest China. Firstly, the data collected by the DCS system of the thermal power plant is preprocessed, including the start-up judgment and LOF algorithm to screen out the data for outliers. Then, the random for-est algorithm is used for feature selection. Finally, the NOx concentration at the SCR denitrification inlet was predicted by Wavenet model, LSTM (Long Short-Term Memory Network) model and SVR (Support Vector Regression) model. The results show that Wavenet performs better in terms of prediction time and evaluation indicators. The mean absolute percentage error (MAPE) is only 1.31%, and the r2 coefficient of determination reaches 0.97. This fully shows that the proposed Wavenet model has relatively good predictive ability.

1. 引言

全球环境污染日益严重，世界各地越来越注重环境保护，NO_x作为环境主要污染物之一，国家对于其在火电厂燃煤锅炉的排放标准也越来越严格。而锅炉脱硝主要是依靠SCR脱硝系统，其需要根据入口NO_x的浓度加入适量的氨水进行处理，因此精确预测SCR脱硝系统入口NO_x的浓度对于脱硝效率而言非常重要。

预测建模通常分为机理建模和数据驱动建模，与SCR脱硝系统入口NO_x浓度相关的指标非常庞杂，因此难以建立准确的机理模型。所以国内外近几年都比较倾向于数据驱动建模。SCR脱硝系统入口NO_x浓度预测作为一个典型的时间序列预测问题，对其的数据驱动建模主要分为两类不同的方法，一是机器学习，目前比较主流的有SVR [1] [2] 、随机森林 [3] 、XGBoost [4] ，机器学习的方法优点是可解释性强、相比于传统的统计学方法做时间预测对非线性相关性处理的更好，但是缺点是单一的机器学习方法比较依赖于特征工程的好坏，计算效率较慢且往往准确性不够高。第二类是神经网络方法，对于时间序列预测问题，前些年许多学者大量使用LSTM [5] [6] [7] 或者GRU [8] [9] (门控循环单元)这种RNN (循环神经网络)，相比于机器学习方法，并不完全依赖于特征工程的好坏，准确度也提高不少，模型预测效果往往不错，但是其特有的循环网络结构，使得计算量较大，导致计算效率低下。因此在因果卷积 [10] 的出现之后，CNN (卷积神经网络)类的方法——Wavenet在时间序列预测方面的应用 [11] 也得以实现。因卷积网络特有的卷积运算，以及空洞卷积的使用，使得计算速度得到大幅度的提升，且相比于单一的LSTM方法，预测精度更高。

为了提高SCR脱硝系统入口NO_x浓度的预测效果，基于提出的Wavenet条件预测 [12] ，提出了一种随机森林–Wavenet预测SCR脱硝系统入口NO_x浓度的模型。首先通过LOF算法 [13] 对数据进行异常点筛除，然后用随机森林算法 [14] 对机理分析后的变量进行特征选择，最后利用Wavenet模型对SCR脱硝系统入口NO_x浓度进行预测。采用西北地区某火电厂的660 MW燃煤机组2022年的数据进行实验，并与LSTM、SVR这两种预测模型做了对比，实验结果表明Wavenet模型具有比较良好的预测效果，且计算效率也更高。

2. 数据预处理及特征选择

整个燃煤锅炉机组长时间运行过程中难免会出现设备故障、节假日休息等特殊情况。如果将所有数据不经处理全部用于神经网络的训练与预测，可能造成模型泛化性较差，预测效果也不会太好，因此需要对原始采集的数据进行异常点筛除及降维。

2.1. NO_x排放的机理分析

对NO_x的生成机理进行分析，可用于初步降维。锅炉燃烧过程中会生成NO_x，其成分主要为NO和NO₂，但是通常NO占了其中的大部分。按照其来源可分为三种氮氧化物：燃料性型NO_x、热力型NO_x、快速型NO_x，影响因素有：① 燃料中含氮量多少，② 过量空气系数；③ 炉内温度。

通过机理分析，我们从DCS系统采集的157个变量变成了包含机组负荷、总风量、二次风门反馈等70余个变量，虽然已经减少了不少变量，但是实验设备有限，这么多变量仍然需要进一步降维才能投入模型中训练。

2.2. 异常值处理

先对数据进行开机判定，通过开机判定的两个条件：1) 机组负荷 > 8；2) 汽机侧转速 > 2900，将未开机时的数据剔除。然后用LOF (局部离群因子)算法 [13] 进行异常值筛选。因为数据是燃煤机组一整年的数据，机组在长期使用过程中难免会出现某些异常情况，因此需要采取合适的方法进行异常点筛选。LOF算法是Breuning [13] 等人在2000年提出的基于密度的识别异常点的方法，其通过定义了一个局部可达密度给出以下公式用于计算每个点的局部孤立程度从而进行异常值筛选：

${\text{LOF}}_{\text{MinPts}}\left(p\right)=\frac{{\displaystyle {\sum }_{o\in N_{\text{MinPts}}\left(p\right)}\frac{lr{d}_{\text{MinPts}}\left(o\right)}{lr{d}_{\text{MinPts}}\left(p\right)}}}{\left|N_{\text{MinPts}}\left(p\right)\right|}$

其中 $N_k\left(p\right)$ 表示p的第k邻域，即所有与p点之间距离都小于p的第k距离的所有点的集合，MinPts表示指定的k， $lr{d}_{\text{MinPts}}\left(p\right)$ 表示点p的第MinPts局部可达密度。在实际应用中，仅需要给定参数k和取一个异常点比例的参数c，然后根据异常点比例确定取异常值的阈值m，当p的局部离群因子 ${\text{LOF}}_k\left(p\right)\ge m$ 时，p被确定为异常点剔除。本文k取20，c取0.1，距离取欧氏距离。将异常值所在的一整行删除，最后余下421,764组数据，用于接下来的实验。

2.3. 基于随机森林的特征选择

高维数据容易引起“梯度爆炸”、模型泛化性差等问题，通过机理分析虽然已经减少了一半的变量，但是仍然有70个变量，这70个变量里面存在不少无关变量以及冗余的变量，保留这些变量对于模型的训练以及测试百害而无一利，因此选择集成式特征选择方法——随机森林对数据接着降维。

随机森林是Breiman [14] 在2001年提出的一种bagging类集成式方法，基于其的特征选择具体步骤如下：

步骤一、通过对原数据集进行有放回的自助采样法获得n个训练集用于训练出n个决策树组成随机森林；

步骤二、对 $\forall$ 决策树 $i\in 1,2,\cdots ,n$ ，计算袋外数据(Out of Bag, OOB)误差，记为 $errOOB{1}_i$ ；

步骤三、对 $\forall j\in 1,2,3,\cdots ,m$ ，m为特征个数，随机对袋外数据中所以样本的特征 $X_j$ 加入噪声干扰，再次计算袋外数据误差，记为 $errOOB{2}_i^{\left(j\right)}$ ；

步骤四、计算特征 $X_j$ 的重要性为 $p_j=\left({\displaystyle \underset{i=1,2,\cdots ,n}{\sum }\left(errOOB{2}_i^j-errOOB{1}_i\right)}\right)/n$ ，将其按照 $p_j/\left({\displaystyle \underset{j=1,2,\cdots ,m}{\sum }{p}_j}\right)$ 计算结果进行降序排序；

步骤五、按照一定比例删除部分排序靠后的特征；

步骤六、将删除后的新数据重复上述所有步骤，直到剩余目标个数的特征。

本文对随机森林的参数选择为：弱学习器即决策树为10,000个，选择回归随机森林，最后得到24个筛选后的变量，见表1。

Table 1. Feature variables after random forest feature selection

表1. 随机森林特征选择后的特征变量

3. 基于Wavenet的NOx排放浓度预测模型

3.1. 基本原理

参考的 [11] 的NARX(p) (p阶非线性自回归外生)结构确定的NO_x排放浓度预测框架：

${\hat{y}}_t=f\left(y_{t-1},\cdots ,y_{t-p},X_{t-1},\cdots ,X_{t-p}\right)$ ， (1)

其中 ${\hat{y}}_i$ 为目标序列的预测值， $f\left(y_{t-1},\cdots ,y_{t-p},X_{t-1},\cdots ,X_{t-p}\right)$ 是目标时间序列 $y_{t-1},\cdots ,y_{t-p}$ 和外生时间序列(即特征变量时间序列) $X_{t-1},\cdots ,X_{t-p}$ 的非线性函数。

使用MSE类型的损失函数，目标函数为：

$E\left(\omega \right)=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(y_i-{\hat{y}}_i\right)}^2}+\frac{\Upsilon }{2}{\displaystyle \underset{l=0}{\overset{L}{\sum }}{\displaystyle \underset{h=1}{\overset{M_{l+1}}{\sum }}{\left(w_h^l\right)}^2}}$ ， (2)

其中 ${\hat{y}}_i$ 为目标序列的预测值， $w_h^l$ 为权重矩阵，右边第二项为L2正则化，用于防止模型过拟合。

$f\left(y_{t-1},\cdots ,y_{t-p},X_{t-1},\cdots ,X_{t-p}\right)$ 是一系列的卷积和非线性激活函数的复合。基础卷积神经网络的结构见图1：

见图1，卷积神经网络相比于全连接神经网络结构是稀疏的，卷积神经网络的权重在每一层上共享，这种结构极大的提高了计算效率。卷积神经网络的权重矩阵也称为滤波器(别称卷积核)，每一层的卷积神经网络是权重矩阵与神经元做卷积。

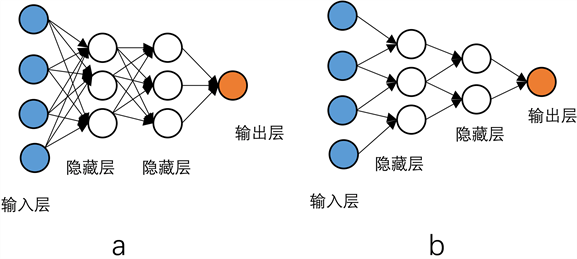
Figure 1. (a) is a fully connected neural network, and (b) is a convolutional neural network

图1. (a)为全连接神经网络，(b)为卷积神经网络

假设输入为 $x=\left(x_0,x_1,\cdots ,x_{n-1}\right)$ ，通过第一层的滤波器 $w_h^1,h=1,2,\cdots ,M_1$ ， $M_1$ 为第一层卷积核的个数，则第一个的卷积输出为：

$a^1\left(i,h\right)=\left(w_h^1\ast x\right)\left(i\right)={\displaystyle \underset{j=-\infty }{\overset{\infty }{\sum }}{w}_h^1\left(j\right)x\left(i-j\right)}$ ， (3)

其中 $w_h^1\in R^{1\times k\times 1}$ ， $a^1\in R^{1\times \left(n-k-1\right)\times M_1}$ ，k为卷积核的尺寸，第一层输出为： $f^1=\sigma \left(a^1\right)$ ， $\sigma$ 为激活函数。 $l=2,\cdots ,L$ ， $f^{l-1}\in R^{1\times N_{l-1}\times M_{l-1}}$ ， $N_{l-1}$ 与卷积核的尺寸有关，而 $M_{l-1}$ 与是l-1层的卷积核的个数，l层的卷积输出为：

$a^l\left(i,h\right)=\left(w_h^l\ast f^{l-1}\right)\left(i\right)={\displaystyle \underset{j=-\infty }{\overset{\infty }{\sum }}{\displaystyle \underset{m}{\overset{M_{l-1}}{\sum }}{w}_h^l\left(j,m\right)f^{l-1}\left(i-j,m\right)}}$ ， (4)

而对于Wavenet模型最主要的部分是其中的因果卷积和空洞卷积，其最初是Oord等人在2016年 [10] 提出的，图2表示了一个四层的因果卷积：

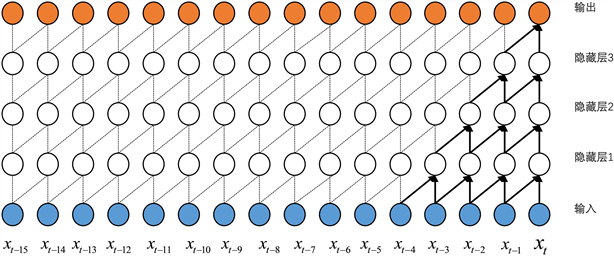
Figure 2. Causal convolution with four layers

图2. 四层的因果卷积

如图2，因果卷积保证了模型在时间t处的预测 $p\left(x_{t+1}|x_1,\cdots ,x_t\right)$ 不会依赖于任何未来时间步 $x_{t+1},\cdots ,x_T$ 的信息，保证了时间序列问题提取信息时的合理性，所以由因果卷积的模型可以处理时间序列问题。但是因为因果卷积的模型，但是因果卷积的感受野(感受野 = 层数 + 过滤器长度 − 1)较小，能提取的信息有限，需要许多层堆叠或者大的滤光片来保证提取到足够长的信息，但是这种方法可能会导致计算量成倍增加。因此 [10] 提出了空洞因果卷积，见图3：

Figure 3. Four-layer void causal convolutional neural network

图3. 四层的空洞因果卷积神经网络

如图3中，空洞因果卷积仅仅用少量的层数即可获得非常大的感受野，同时保留了输入信息的完整性，极大的提高了计算效率。这得益于空洞卷积提出的扩张率，如上图所示以指数增加的扩张率会让感受野随着层数呈指数增长，空洞因果卷积的感受野计算方式为： $r=2^{L-1}k$ ，其中L为网络层数，k为过滤片的尺寸。第l层空洞因果卷积的输出为：

$\left(w_h^l\ast {}_{d}f{}^{l-1}\right)\left(i\right)={\displaystyle \underset{j=-\infty }{\overset{\infty }{\sum }}{\displaystyle \underset{m=1}{\overset{M_{l-1}}{\sum }}{w}_h^l\left(j,m\right)f^{l-1}\left(i-d\cdot j,m\right)}}$ ， (5)

其中 $d=2^{L-1}$ 为扩张率。

3.2. 模型建立

由公式(1)可知每个 $y_t$ 的预测值 ${\hat{y}}_i$ 都是由非线性函数 $f\left(y_{t-1},\cdots ,y_{t-p},X_{t-1},\cdots ,X_{t-p}\right)$ 确定的，而这个非线性函数即我们的Wavenet模型，其主要结构见图4：

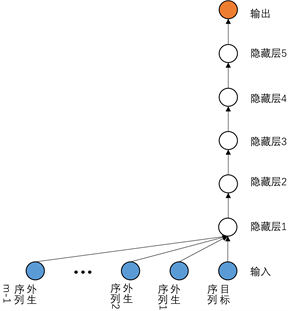
Figure 4. Wavenet neural network model stacked with 6-layer

图4. 堆叠了6层的Wavenet神经网络模型

以上预测模型考虑了外生时间序列的影响，但仅仅在第一层将外生时间序列和目标时间序列分开处理，从第二层到最后一层都合并处理。

Wavenet模型的具体结构见图5、图6、图7：

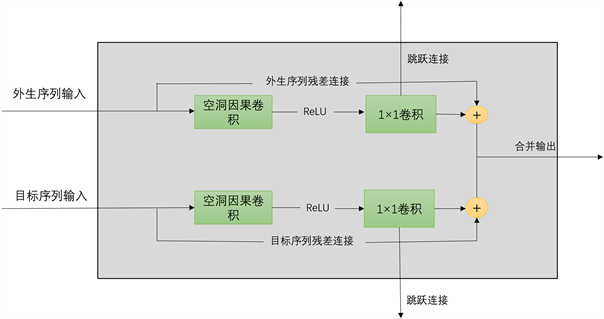
Figure 5. Structure of the first layer of Wavenet

图5. Wavenet第一层的结构

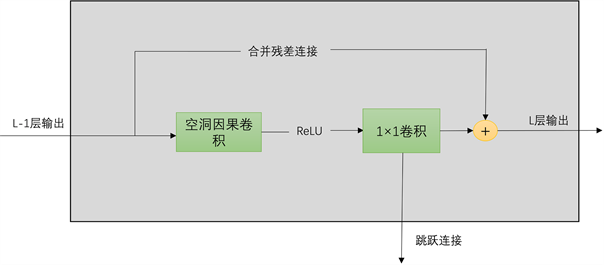
Figure 6. Structure of layers 2 to 5

图6. 第2层到第5层的结构

Figure 7. Structure of the output layer

图7. 输出层的结构

如图5、图6，每一层的残差连接之后的输出作为下一层的输入，每一层一维卷积后的跳跃连接到输出层。前五层都使用ReLU作为扩张因果卷积的激活函数。最后一层见图7，选择Linear作为激活函数。其中一维卷积网络用于残差连接和跳跃连接时的维度一致。因为每一层的结果都进行了跳跃连接，在最后的输出层可将每一层结果进行逐元素相加后再通过激活函数和一个1 × 1的卷积进行输出最后的预测结果。每一层的跳跃连接可以加快收敛速度，而残差连接保证了可以堆叠更多层而不发生梯度爆炸问题。

4. 实验过程和结果

本文采用Wavenet对NO_x排放建立了预测模型，取时间长度为p = 64，Wavenet本质上是属于CNN (卷积神经网络)类的方法，为了显示模型性能的好坏，选取了RNN(循环神经网络)类的方法LSTM (长短期记忆网络)与机器学习类的方法SVR (支持向量回归)。因为p = 64，滤光片大小为2，Wavenet按照空洞卷积的规则一共堆叠了6层，优化器选择Adam，初始学习率为0.005，正则化参数为0.05；LSTM选取64个隐藏节点，只有一层时间步长也取64，优化器取Adam，初始学习率为0.005；SVR的核函数取RBF函数， $\epsilon$ (目标误差)取0.01，C (惩罚系数)取4.56， $\gamma$ (核函数的系数)取0.7。

数据处理

本文按照7:2:1的比例划分训练集、验证集、测试集。为了在训练时更快收敛，需要对数据的每一列先进行归一化处理：

$\hat{x}=\frac{x-x_{\min }}{x_{\max }-x_{\min }}$ (6)

按照图8的方法将归一化后的特征变量数据和目标变量数据分别处理成 $l\times p\times \left(m-1\right)$ 和 $l\times p\times 1$ 的时间序列结构：

Figure 8. Time series processing

图8. 时间序列处理

其中l为序列长度，p为滑动窗口长度，m为特征变量维度，将处理好的时间序列按照128的批次放入Wavenet模型中进行训练，设定为最多1000次迭代：

如图9，模型收敛很快，训练集和验证集大概在20次左右就已经收敛了，而且每次迭代时间仅为19 s，计算效率较高。

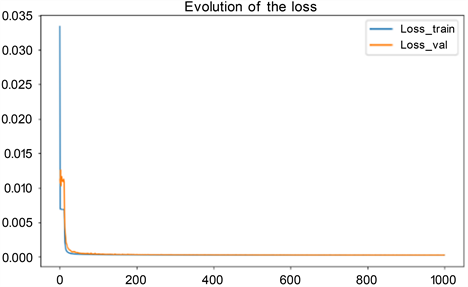
Figure 9. Epoch decline plot of training set loss and validation set loss

图9. 训练集损失与验证集损失关于Epoch下降图

基于Wavenet模型在测试集上的预测结果见图10：

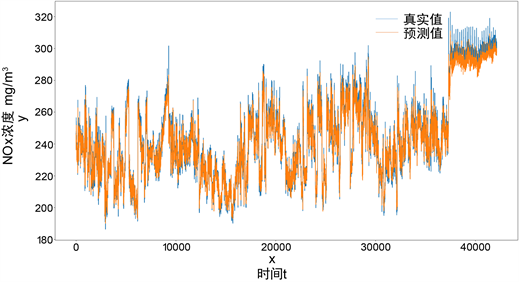(a)(b)

Figure 10. (a) is the fitting diagram of the test set, and (b) is the fitting diagram of one of the segments

图10. (a)为测试集拟合图，(b)为截取其中某一段拟合图

由上图10可知，Wavenet模型拟合效果比较好，同时其具有高效的计算效率，但是只是根据拟合图我们没办法得到预测的量化结果，因此对Wavenet模型以及对比模型的NO_x浓度预测值与真实值分别计算了四种评价指标——RMSE (均方根误差)、MAE (平均绝对误差)、MAPE (平均绝对百分比误差)、R²决定系数，实验结果见表2：

Table 2. Comparison of evaluation indicators

表2. 各项评价指标对比

时间对比见表3：

Table 3. Comparison of the iteration times of each round

表3. 每轮迭代时间对比

5. 结论

通过实验及对比实验，得到：1) Wavenet模型与LSTM模型、SVR模型相比较，其计算效率更高，计算成本更低，预测效果最好。均方根误差(RMSE)仅为4.27，满足燃煤锅炉排放实际生产需要。且Wavenet采用的空洞因果卷积既能保证解决时间序列问题的合理性，又能极大的提高计算效率，所以从各方面来讲，本文的预测模型有着不错的效果。2) 特征工程往往能够使得计算量大幅降低，但由于实验条件有限，未做是否进行特征选择的对比实验，未能得到除了关于特征工程对预测精度的提升是否有明显效果。