基于WT-SA-LSTM的降水量预测

Precipitation Prediction Based on WT-SA-LSTM

摘要: 监测和预测降水量对于农业、水资源管理、气象灾害预警等方面都至关重要。本文利用1991~2020年江西省九江市10个地面气象观测站月降水量实测数据，建立SARIMA、随机森林、LSTM降水量预测模型。结果表明，LSTM模型的MSE、MAPE、R方分别为0.0101、7.76%、0.7971，比SARIMA、随机森林误差低；其次，在LSTM模型的基础上，加入小波变换理论和模拟退火算法，将三者结合并运用在月降水量预测中得到WT-SA-LSTM模型，该模型MSE、MAPE、R方分别为0.0082、5.78%、0.8454，预测效果比单一的神经网络模型误差MSE、MAPE分别降低19.8%、25%，R方提高了4.9%。

Abstract: Monitoring and forecasting precipitation holds great importance in various fields including agriculture, water management, and meteorological disaster warning. This paper focuses on the measured monthly precipitation data from 1991 to 2020 of 10 surface meteorological observa-tion stations in Jiujiang City, Jiangxi Province. The study aims to establish a precipitation prediction model using SARIMA, random forest, and LSTM. The results showed that the MSE, MAPE, and R-squared of the LSTM model were 0.0101, 7.76%, and 0.7971, respectively, which were lower than those of the SARIMA and random forest models. Secondly, based on the LSTM model, the WT-SA-LSTM model was developed by combining wavelet transformation theory and simulated annealing algorithm, and applied to monthly precipitation forecasting. The MSE, MAPE, and R-squared of the WT-SA-LSTM model were 0.0082, 5.78%, and 0.8454, respectively, and the predictive performance was better than that of the single neural network model with a decrease of 19.8% and 25% in MSE and MAPE, respectively, and an increase of 4.9% in R-squared.

1. 引言

降水量是一个非常重要的气象要素，过多或过少会直接对生产和生活产生影响。降雨量过大会导致山体滑坡、泥石流等伴生自然灾害；而降水量过低时又会引发干旱等生态环境问题，影响农作物正常生产，同时也会导致居民用水困难，进而影响其他工业生产。因此，根据某地历史降水量数据，选择合适的模型或者方法准确预测当地降水量，以便提早做好预防工作，减少洪涝或者干旱气候对人民生产和生活的影响 [1] 。

传统的降水预测方法大概可以分为三种：动力学、统计学、统计–动力结合的方法，很多学者基于这些方法对局部地区建立了降水预测模型。但是，因为降水数据拥有很强的周期性、相关性、不确定性，用传统的方法对降水进行预测会遇到很多困难 [2] 。所以，可以看到越来越多的学者尝试用机器学习中的方法进行预测，其中常见的机器学习算法有支持向量机、随机森林算法、BP神经网络等。随着计算能力的提高以及深度学习技术的发展，大量学者开始又运用不同的深度学习算法进行研究。目前，最常用的深度学习方法包括卷积神经网络、LSTM和基于多特征的BP神经网络、RNN等，它们在降水预报方面都有很好的效果。例如，葛玉辉等人结合小波变换和BP神经网络对GPS可降水量进行了预测 [3] ，通过将小波基函数替换BP神经网络中常用的激活函数，使模型同时具有小波变换和神经网络的良好特性，结果表现出更好的容错性和逼近能力。谢劭峰等人结合遗传算法和BP神经网络对可降水量进行了预测 [4] ，他利用遗传算法优化了BP神经网络学习速度慢，容易出现如局部极值的缺点，结果表明该模型预测能力更精确。刘新等人建立了LSTM、RNN、ARIMA等五个模型，并分别在青藏高原进行了月降水量的预测和结果分析 [5] ，结果表明五个预测模型中LSTM均方根误差和平均绝对误差均最低。郭宝丽利用灰色波形与小波BP神经网络模型的组合模型对重庆市的年降水量进行了预测 [6] ，并且与单个的模型结果进行了比较，结果证明组合模型的预测效果较好。陈沪生等人结合小波变换和ARIMA模型对黄山市1957~2016年间的年降水量进行了预测 [7] ，结果表明该组合模型预测降水量表现较好，但在降水量异常年份误差较大。以上研究表明，使用深度学习方法进行预测准确率更高。本文通过建立SARIMA、随机森林、LSTM、WT-SA-LSTM四种模型，分别对该地区进行月降水量预测，最后把结果进行对比分析，找到适用于江西省九江市的月降水统计预测方法，并应用于该地区。

2. 数据来源和方法介绍

2.1. 研究区域

本文选取江西省九江市月总降水量作为研究对象。九江市位于长江中游的上游，地理位置十分重要。由于九江市天气易变，乍暖乍寒，夏季主要受南风的影响，带来了高温和湿润的气候，容易出现强降水和雷雨天气，冬季则受北风的影响，带来了相对较干燥的气候，容易出现干旱。这种特点对于当地的生态环境、农业生产和人类活动都产生了深远的影响，因此分析该地区的降水量及进行下一时段的预测对九江市的可持续发展具有重要的意义。

2.2. 资料来源

本文使用的数据为九江市10个站点的1991年~2020年月总降水量数据，总共3600个，本文所涉及到的实验均按照9:1的比例来构造训练集和验证集。

本文以九江市九江站为实验对象，其中1991年1月~2017年12月总共324个数据作为训练数据用来拟合模型，2018年1月~2020年12月共36个数据作为测试数据用来优化校验模型。

Figure 1. Total monthly precipitation at Jiujiang Station over the past 30 years

图1. 九江站三十年月降水总量

图1展示了九江站的月总降水量数据。从图中可以看到，这些数据呈现出季节变化的趋势，但是也有个别的异常值，所以在实验前要对异常数据进行剔除，再利用三次样条插值法进行插值。

3. 方法介绍与评价指标

3.1. SARIMA模型原理介绍

ARIMA模型是一种常用的时间序列分析模型，但是由于ARIMA模型有两个缺点：1) 要求数据具有平稳性和同方差性等性质。2) 无法处理长期趋势。所以用该模型对月降水量进行预测时，效果会比较差。因此我们使用改进后的模型(SARIMA)进行预测。

季节性差分自回归滑动平均模型(Seasonal Autoregressive Integrated Moving Average, SARIMA)是ARIMA模型的改良模型，它是在ARIMA模型的基础上增加季节性周期参数演变而来，常用于具有长期趋势和明显的季节性趋势的时间序列的预测 [8] 。这个模型的实质上是先对 $y_t$ 进行逐期差分，先去掉周期序列的趋势性，而后实行季度差分，再去掉季度性。后经以上所述处理过程，所形成的模型就可以表示为： $\text{SARIMA}\left(p,d,q\right)\ast \left(P,D,Q,S\right)$ ，假设 $y_t$ 表示时间序列在时间点t的观测值，其中t表示离散的时间点

$y_t=AR\left(p\right)+I\left(d\right)+MA\left(q\right)+SAR\left(P\right)+SI\left(D\right)+SMA\left(Q\right)+\epsilon (\; t\; )$

其中：

$AR\left(p\right)$ ：p阶自回归项，表示当前观测值与前p个时间步长的观测值之间的线性关系。

$I\left(d\right)$ ：d阶差分项，用于消除非季节性趋势。

$MA\left(q\right)$ ：q阶移动平均项，表示当前观测值与前q个白噪声(随机误差)项之间的线性关系。

$SAR\left(P\right)$ ：P阶季节性自回归项，考虑时间序列在季节性周期上的相关性。

$SI\left(D\right)$ ：D阶季节性差分项，用于消除季节性。

$SMA\left(Q\right)$ ：Q阶季节性移动平均项，考虑时间序列在季节性周期上的随机误差项之间的相关性。

$\epsilon \left(t\right)$ ：表示白噪声误差项，假设是平均为零、方差为常数的随机误差。

3.2. 随机森林

随机森林(Random Forest, RF)是以决策树为基学习器，然后构建Bagging集成，最后进一步在决策树的训练过程中引入随机属性的选择。随机森林算法简单、易于实现、计算开销小，在很多现实任务中展现出强大的性能 [9] 。在RF模型中，建立了多棵决策树(每棵决策树都是随机生成且相互独立的)，最后将多棵决策树的建模结果求平均来得到最终结果。图2是是建模过程。

Figure 2. Random forest principle

图2. 随机森林原理

3.3. 长短期记忆神经网络

LSTM (Long Short-Term Memory, LSTM)网络是一种特殊的循环神经网络(Recurrent Neural Networks)，它在处理时间序列数据时，可以很好地解决长期依赖问题。

LSTM模型通过引入记忆单元和三个门控机制来解决长期依赖问题。记忆单元负责存储序列信息，三个门控机制(遗忘门、输入门、输出门)则可以控制记忆单元的读写和保留程度，从而允许模型选择性地忽略不重要的信息 [10] 。图3是用图来表示这个过程。

Figure 3. LSTM mechanism diagram

图3. LSTM机理图

3.4. 小波变换与重构

小波变换(wavelet transform, WT)继承和发展了短时傅立叶变换局部化的思想，同时又克服了窗口大小不随频率变化等缺点，是进行信号时频分析和处理的理想工具。

Figure 4. Monthly precipitation wavelet decomposition diagram at Jiujiang Station

图4. 九江站月降水小波分解图

其主要步骤如下：

1) 选择小波函数：选择适合问题的小波函数，通常需要考虑时间序列数据的性质和分析需求。不同的小波函数适用于不同类型的时间序列数据，比如Haar小波适用于较简单的数据，而Daubechies小波适用于平稳的数据 [11] 。

2) 分解过程：将时间序列数据进行多层小波分解。分解过程中，时间序列数据在不同尺度上被逐层分解成低频部分(近似系数)和高频部分(细节系数)。

3) 滤波和下采样：在时间序列数据的分解中，低频部分通过滤波器进行平滑，得到下一层的低频部分，同时也得到该层的高频部分。

4) 阈值处理：高频部分通常包含噪声和细节信息。

5) 重构过程：从最深层的低频部分和高频部分开始，通过逆向的滤波和上采样操作，逐层将时间序列数据重构回原始尺度。这样可以获得不同尺度上的趋势、周期和噪声等信息。

6) 重构原始时间序列：将经过阈值处理的近似系数和细节系数进行逆向重构，得到去噪后的时间序列数据。

我们以九江站月总降水量为例，经过小波分解后的如图4所示。

3.5. 模拟退火算法

模拟退火(Simulated Annealing, SA)是基于蒙特卡罗迭代求解策略的随机寻优算法，基于物理中固体物质的退火过程与组合优化问题(NP完全问题)的相似性。该算法在遗传算法上做了一些改进，它的搜索过程用到了Metropolis准则，也就是允许在搜索过程中一些“差”解有一定的概率被接受，为了避免陷入局部最优解，然后随着时间的推移逐渐降低接受“差”解的概率，使算法最终趋向于收敛到全局最优解 [12] 。

其步骤如下：

1) 设定初始温度T₀，终止温度T_f，降温速度0 < rate < 1，T₀要取的很高，相当于加温到很高的温度。T_f要取的很小，相当于基态，rate越大，降温越慢。取一个起始点x，算出函数值 $f\left(x\right)$ 。

2) 当T₀ > T_f，时，随机让x移动，计算新的函数值 $f\left(x+1\right)$ 。

3) 根据Metropolis准则进行判断：

a) 如果新值 $f\left(x+1\right)$ <当前值 $f\left(x\right)$ ，以概率1把当前值更新为新值；这很好理解，如果你发现移动到的新点求出来的值更小，肯定要更新当前值；

b) 如果 $f\left(x\right)$ > $f\left(x+1\right)$ ，计算概率 $P=\exp \left(-\frac{f\left(x+1\right)-f\left(x\right)}{T_0}\right)$ 。取一个随机数0 < r < 1，当r < P

时把当前值更新为新值，否则不更新。可以发现，当前温度T₀越大，指数函数括号里的值越大，接受这个新值的概率P越大。随着迭代次数的增加T₀会越来越小，接受新值的概率P也会越来越小，相当于渐渐冷却了下来，趋于稳定的状态。

4) 进行一次降温： $T_0=T_0\ast rate$ ，转到步骤2)。

3.6. 模型评价指标

在上述模型中，选取的量化评价指标为均方误差、平均绝对百分比误差、决定系数。

1) 均方误差(Mean Absolute Error, MSE)表示预测值与真实值的绝对平方误差的平均值，范围[0, +∞)，MSE的值越小，说明预测模型效果产生的误差越小。

2) 平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)表示偏离的相对大小(即百分率)，范围[0, +∞)。MAPE的值越小，说明预测模型拥有更好的精确度。

3) 决定系数(Coefficient of Determination, R方)衡量的是预测值对于真实值的拟合好坏程度，其取值范围为[0, 1]。R方越大，表示模型拟合效果越好。

4. 预测结果展示与分析

4.1. SARIMA降水预测模型

用SARIMA模型进行时间序列预测时，首先需要对时间序列进行平稳性检验和白噪声检验，用以判断是否需要差分、是否含有季节性因素，并根据检验结果确定参数d、D和S的取值。其次，为SARIMA模型定阶，根据AIC准则或BIC准则确定p、q、P和Q的取值，得到 $\text{SARIMA}\left(p,d,q\right)\ast \left(P,D,Q,S\right)$ 模型，最后进行预测。通过实验我们得出，当 $p=3$ ， $d=0$ ， $q=4$ ， $P=1$ ， $Q=2$ ， $D=0$ ， $S=12$ 时，模型的拟合效果最好。

图5是2018年1月~2020年12月真实值与预测值的对比图。

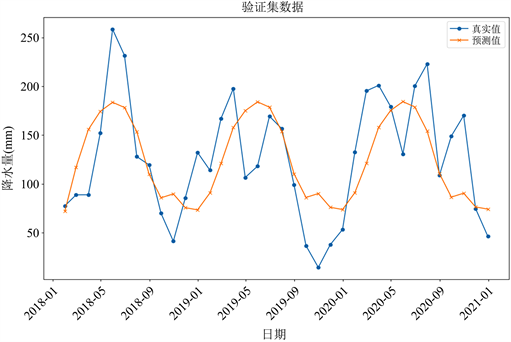
Figure 5. SARIMA model predicted value vs. true value

图5. SARIMA模型预测值与真实值对比

由图5可以看出，该预测结果并不理想。总体上看，SARIMA模型能预测出月总降水量的周期特征，少部分月份预测值比较准确，但是大多数情况下预测值与真实值误差比较大。其原因是SARIMA模型适合于短期预测，所以当面对长期预测时，准确率会比较低。

4.2. 随机森林预测模型

由于月降水总量数据具有明显的季节性趋势，所以我们先对数据进行预处理，常用的去趋势性的方法有两种：季节差分和移动平均。在这个模型中，将数据进行移动平均处理，然后再用随机森林模型进行预测，得到图6预测结果。

在该模型下，我们可以看到，RF模型可以预测出来月降水的大致趋势，但是真实值与预测值的误差比较大，且存在滞后现象，所以导致利用该模型预测的准确度也较低。

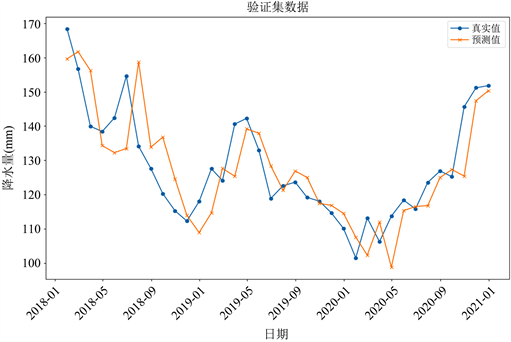
Figure 6. RF model predicted value vs. true value

图6. RF模型预测值与真实值对比

4.3. 长短期记忆网络预测模型

LSTM的主要优点是能够有效地处理长序列数据。通过引入门控机制和细胞状态，能够在较长的时间跨度上保持信息，从而捕捉到长期依赖关系。解决了上述两个模型遇到的问题。

该模型进行预测时的一般步骤：

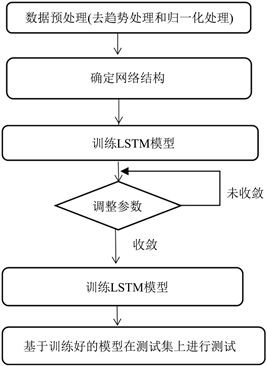
在LSTM模型内部中，激活函数有ReLU、ReLU6、Sigmoid、Tanh、LogSigmoid、Softmax、PReLU、Softmin等。优化器有Adam、SGD、Adagrad、RMSProp等。经过多次实验发现，当使用sigmiod函数作为激活函数，Adam作为优化器，模型的预测效果最好，其他的参数设置如下表1所示。

Table 1. Optimal parameters

表1. 最优参数

由最优参数构建的LSTM模型进行月降水总量预测，预测值与真实值对比如图7所示。

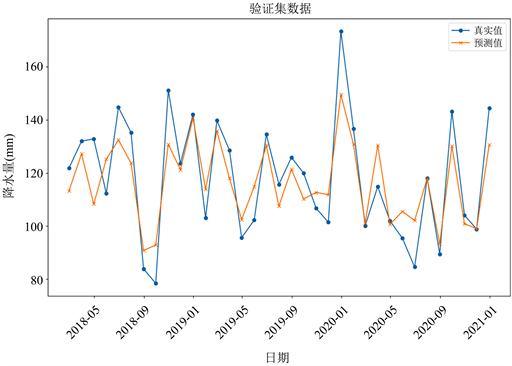
Figure 7. Comparison between the predicted value and the true value of the LSTM model

图7. LSTM模型预测值与真实值对比

从图7中我们可以看出，LSTM模型已经很好拟合了月总降水量数据变化的趋势，并且使用该模型进行预测的结果与前两种方法相比，精度有很大的提高，接下来我们尝试在LSTM模型的基础上进行改进。

4.4. WT-SA-LSTM模型

首先，我们先用小波变换对原始时间序列数据进行重构，然后把重构后的数据作为LSTM模型的输入数据，最后再通过用模拟退火优化算法找出这个组合模型的最优解。图8为组合模型的预测值与真实值的对比。

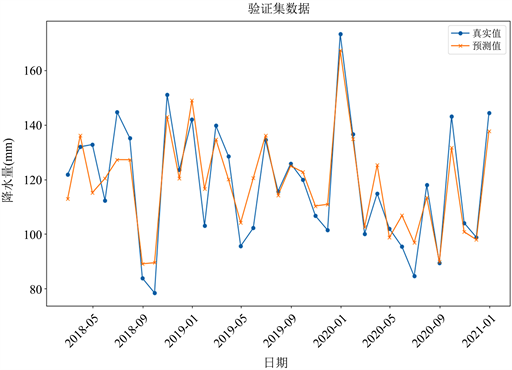
Figure 8. Comparison between the predicted value and the true value of the WT-SA-LSTM model

图8. WT-SA-LSTM模型预测值与真实值对比

由实验结果可知，该模型预测效果比单一的LSTM精度更高一些。

5. 结果对比

对九江市站点预测了三次，取三次评价指标的平均值为最终结果。表2为四种模型的评价指标值。

Table 2. Evaluation indicators of each model

表2. 各模型评价指标

实验结论：基于WT-SA-LSTM月降水量预测模型，对具有周期性和波动性特征的月降水量数据具有较好的学习和预测效果。

由上述实验结果对比可知，常见的机器学习预测模型对于月降水量这种波动性较大的时间序列进行预测时，只能预测出变化趋势，预测值的准确度比较低，产生的误差较大。用LSTM模型可以明显提高预测的精度，由于小波变换能够同时提取时间序列的时域和频域特征，在引入小波变换后，模型的预测精度也有了进一步的提高。把该模型应用于剩下的九个站点，得到的结论如表3所示。

Table 3. Evaluation index values of the combined model of each site

表3. 各站点组合模型评价指标值

6. 总结

降水量预测一直是气候领域的一个重要研究方向，但是降水量容易受到地势、环境以及大气层等多种因素的影响，具有明显的周期性特征和较大波动性特征 [13] 。使用传统基于统计学的模型或回归方法并不能对月降水量数据进行有效预测，为了提高月降水量的预测精度，本文通过研究基于LSTM的预测模型和小波变换理论，又加入了模拟退火这一优化算法，将三者结合并运用在月降水量预测中，实验结果表明：单一的SARMA模型、随机森林模型和LSTM模型预测效果较差，将小波变换、模拟退火算法与LSTM模型结合后的预测精度有了较高的提升，这为月降水量预测的研究提供一种新的思路，有一定的参考价值。

基金项目

国家自然科学基金面上项目(62076137)。