1. 引言
玻璃材料具有良好的耐高温、耐腐蚀和透光性能,在工艺品、建筑行业以及汽车领域中起着重要的作用。如汽车风挡玻璃,在行人头部保护系统中占据重要的位置,在大多数情况下行人头部直接承受与玻璃碰撞的伤害,此时玻璃的吸能性能优化至关重要,特别是PVB夹层在冲击过程中的作用 [1] 。目前玻璃在结构耐撞性的研究很多,而面对爆炸冲击载荷下的性能响应有些欠缺。由于爆炸的瞬间能产生巨大的冲击力,玻璃往往无法抵抗吸收这部分能量而破裂并造成大量飞溅的玻璃碎片,在模拟玻璃飞溅过程的建模中是困难的。因此,能真实有效地反应玻璃裂纹扩展的动态响应具有很高的价值。
面对爆炸冲击载荷,玻璃作为一种脆性材料无法满足抗爆需求,而PVB夹层玻璃能有效地弥补这一缺陷。PVB胶是超弹性的材料,能进一步吸收冲击能量,并尽可能粘连玻璃碎片,仅仅使玻璃产生裂纹,极大地保护了人员的安全。林德佳等采用PVB胶的结构性能,提出一种内聚力模型,并有效验证了夹胶玻璃的损伤行为 [2] 。李峰等研究玻璃幕墙在爆炸载荷作用下的动态响应,分别考虑爆炸载荷与风载或地震载荷作用,并分析和对比了玻璃幕墙的受损机理 [3] 。本文采用LS-Dyna软件建立爆炸冲击下夹胶玻璃的有限元模型,其中包括空气域、炸药以及PVB夹层玻璃。本文主要研究了小型炸药位于单层玻璃中部玻璃的损伤变化,以及不同当量的炸药下夹胶玻璃的动态响应。基于仿真结果,本文建立的玻璃损伤模型能反应玻璃裂纹的扩散趋势。
2. 数值模拟
2.1. 爆炸冲击理论
爆炸是一种极端的物理现象,通常由物质迅速发生高温高压气体的化学反应而引起。这种反应以惊人的速度进行,并伴随极高温度和成千上万大气压的冲击压力释放,同时产生显著的声波。爆炸可以分为几种主要类型,包括物理爆炸、化学爆炸和核爆炸 [4] 。物理爆炸是由高压容器内部压力超过容器承受限制或容器结构瞬间损坏引发的。化学爆炸则是由可燃物质与氧气之间迅速发生的剧烈化学反应引发的。与之不同,核爆炸的能量来自于核裂变或核聚变反应释放的核能。核爆炸的威力远远超过物理和化学爆炸,其释放的高温、高压和辐射对人类和环境带来极大的破坏和威胁。本文所研究的爆炸属于是化学爆炸。
由于炸药爆炸的瞬间释放出巨大能量,将爆炸气体迅速升至几千度并快速膨胀,最后以冲击波的形式传播。反应过程中,释放的能量越多,冲击传播的速度越快,爆炸的强度越高。炸药爆炸的化学反应过程中,必然伴随着大量的气体等产物,并且这类爆轰产物的体积远大于原始的炸药体积。因此爆轰产物以极高的传播速度不断地向周围扩散,空气内部不断地膨胀,将爆炸物内的势能转变成为爆轰产物的动能。
在空气介质中的炸药爆炸,释放的热量在极短的时间内使空气膨胀并产生高温高压,由于空气初始的压力与膨胀后的压力差生了压力差,并且爆轰产物的剧烈膨胀,进一步的压缩周围的空气,在空气中形成了爆炸冲击波。根据爆炸的经验公式和相关研究,经典的自由域内爆炸冲击波与时间的传播历程曲线如图1所示。在爆炸初始阶段,冲击波还未与空气内的介质发生接触,此时气体表面的压强为P0,在爆炸产生后,经过一段时间ta,空气内的压强迅速上升了Pl,此时爆炸压强为P0 + Pl,Pl为超压峰值,并在tβ的时间段内以指数形式衰减至初始压强。由于惯性力的作用,爆炸压强持续下降到负超压峰值,随后经过一段时间的调整慢慢恢复到大气压强,因此整个冲击过程可以分正压时段和负压时段。从图1中可以看出,负压的峰值远小于正压的峰值,而且获取负压的数据比较困难,因此通常情况下忽略负压的影响,并通过Friedlander的经验公式近似描述爆炸冲击波的历程曲线 [5] :
(1)
其中P0表示为大气压强,Pl表示为正超压峰值,ta表示为气体未发生膨胀阶段,tβ表示为正压阶段,r表示为气压衰减因子。
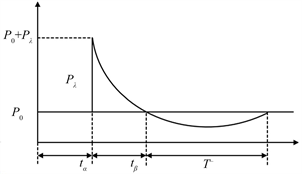
Figure 1. Variation curve of explosion shock wave pressure
图1. 爆炸冲击波压强变化曲线
2.2. 有限元模型的建立
2.2.1. 几何模型网格划分及边界条件
本文在Hypermesh软件中建立了爆炸冲击下玻璃的有限元模型,包括单层玻璃和PVB夹层玻璃。如图2,其中(a)为直观反应单层玻璃在冲击下的裂纹扩散趋势,玻璃尺寸为100 cm × 100 cm × 1 cm,炸药当量为10 g并放置于玻璃中心,玻璃表面设置空气网格,玻璃周围固定约束。而在(b)中,玻璃的尺寸为100 cm × 100 cm × 3 cm,厚度方向划分2层单元,PVB胶的厚度为0.38 cm放置在内外层玻璃之间,固定玻璃四周,炸药放置在玻璃外层上方50 cm,炸药当量30 g,整个夹胶玻璃位于空气网格中,并在空气网格表面增加非反射属性,模拟现实的空气环境。由于炸药在特定的场合中所需的形状不同,如圆柱形、球形和方形等,导致在空气网格内划分炸药网格的难度上升,因此,本文采用体积填充法对炸药进行建模,与划分炸药实体网格相比,大大的提升了建模效率,并且通过“Initial Volume Fraction Geometry”卡片可以随时修改炸药的形状尺寸参数等,有效的解决炸药重新建模的问题。
 (a)
(a)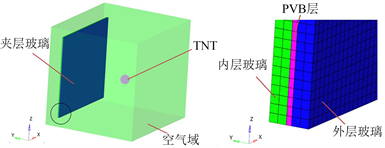 (b)
(b)
Figure 2. Finite element model of glass response under blast impact: (a) Single pane glass; (b) PVB laminated glass
图2. 爆炸冲击下玻璃响应有限元模型:(a) 单层玻璃;(b) PVB夹层玻璃
本文在Hypermesh中采用“Flanagan-Belytschko stiffness form”积分单元对夹胶玻璃进行建模,其中玻璃和PVB胶层均为实体单元,为提高计算的精度,均划分为六面体单元。基于刚度的沙漏控制来避免杂散的零能量变形模式,并通过降低积分来避免体积锁定,玻璃内接触采用“Automatic Surface to Surface”以避免相互穿透。为保证模型仿真过程的收敛性,玻璃的网格尺寸划分为1 cm,空气网格的尺寸为2 cm。本文采用拉格朗日–欧拉算法对爆炸冲击过程进行建模,其中PVB夹层玻璃采用拉格朗日算法,空气和炸药使用欧拉算法,并采用流固耦合的方式处理玻璃在冲击过程中的反应。整体模型采用统一单位g-cm-us。
2.2.2. 材料模型
玻璃是一种典型的脆性材料,在承受冲击力或压缩力时强度高,但在承受拉力时强度相对较低。本研究采用Johnson-Holmquist (JH-2)模型模拟了玻璃等脆性材料在爆炸冲击力作用下的损伤劣化行为。JH-2模型可以有效地描述玻璃在高能冲击下的断裂和碎裂 [6] 。为了模拟玻璃损坏后的破碎现象,采用主应力破坏准则进行模拟,玻璃材料应力大小为80 Mpa。
JH-2本构模型中材料的状态方程可以表示为:
(2)
(3)
其中p表示为静水压力,K1表示为材料的体积模量,K2和K3都是常量,μ表示为体应变,ρ表示为现在密度,ρ0表示为初始密度。
JH-2构造模型的强度准则是将材料应力表示为静水压力的数值关系,其中材料应力用等效应力比表示:
(4)
其中σHEL表示为材料弹性极限处的应力。与损坏系数D相关的等效应力比和材料强度模型表示为:
(5)
其中
表示为未受损时的等效应力,
表示为受损时的等效应力,D表示为损伤因子(0 < D < 1) [7] 。玻璃的材料特性和JH-2参数见表1。

Table 1. Material properties of glass and JH-2 parameters
表1. 玻璃的材料特性和JH-2参数
PVB胶是优良的超弹性材料。夹层玻璃结构在承受巨大的能量冲击时,PVB层起着重要作用。当玻璃损坏时,PVB层仍能承受冲击,防止玻璃碎片飞溅,解决了玻璃损坏应变小的问题,提高了玻璃的安全性能。本文采用Mooney-Rivilin-Rubber模型来描述PVB胶层的材料特性。应变能量密度方程表示为:
(6)
其中An、Bn、Cn和Dn都是常数,I1、I2和I3都是不变张量。PVB的材料特性见表2。

Table 2. Material parameters of PVB
表2. PVB胶的材料参数
空气采用MAT-NULL模型建模,并与状态方程EOS-Linear-Polynomial相互作用模拟真实环境。为提高仿真结果的计算速度,本文将空气看作为理想气体。空气的材料参数如表3所示。空气的状态方程可以描述为 [8] :
(7)
其中P2表示为大气压强,E0表示为单位体积能量,C0到C6都是常数,其中C0到C4值为0,C5 = C6 = 0.4 MPa。

Table 3. Material parameters of air
表3. 空气的材料参数
为更好的模拟出爆炸冲击反应,本文采用Ls-Dyna软件模拟炸药的性能,其中MAT-HIGH-EXPLOSIVE-BURN可以有效的描述炸药的参数性能。本文采用TNT炸药模型进行模拟,TNT的材料参数如表4所示。

Table 4. Material parameters of TNT
表4. TNT的材料参数
3. 结果分析
3.1. 单层玻璃的爆炸模拟
本文在2.2节中建立单层玻璃在爆炸冲击下的数值模型,采用单元删除法模拟玻璃的裂纹扩散。该方法当单元达到预定的失效应力值时,计算过程中会将其删除,此时玻璃开始表现裂纹状,并随时间不断扩展。本节设置TNT当量10 g,爆炸持续时间设置为2 ms,玻璃单元失效应力值为80 Mpa。单层玻璃在爆炸冲击下的损伤云图如图3所示。
从图3中可以看出,TNT在爆炸瞬间往周围释放能量,以圆弧形式扩散。在0.1 ms时,玻璃破碎并产生飞溅的玻璃碎片,并且玻璃单元达到预设失效的应力值后直接删除,到0.2 ms时,玻璃出现径向裂纹并不断传播,直到2 ms时,玻璃停止破裂,符合玻璃裂纹产生的规律。图3中单层玻璃损伤结果表明,单元删除法可以有效预测玻璃在爆炸冲击下的裂纹响应。因此本文将单元删除法应用在PVB夹层玻璃中。

Figure 3. Damage cloud of single-pane glass under blast impact
图3. 单层玻璃在爆炸冲击下的损伤云图
3.2. PVB夹层玻璃的爆炸模拟
由3.1节已知单元删除法的可行性,因此在PVB夹层玻璃中设置相同的单元失效参数,TNT当量为30 g,本节中将对PVB夹层玻璃进行不同工况的响应分析,仿真工况如表5所示。

Table 5. Different working conditions at 30 g equivalent of TNT
表5. 30 g当量TNT下不同工况
在相同TNT当量下,爆炸距离对外层玻璃有直观的影响,因此为更好的研究玻璃在爆炸冲击下的响应,从以上四种工况对玻璃损伤进行分析,爆炸结束时间设置为5 ms。
数值模拟可以有效的反应爆炸冲击能量对夹层玻璃的裂纹扩展响应,爆炸冲击波的传播曲线随着爆炸距离的变化如图4所示。从图4可以看出,爆炸距离越远,冲击波的压强传播到玻璃后响应的时间增长并且能量也不断地下降。TNT爆炸后,冲击波持续压缩空气并扩散,到达被测物周围空气的瞬间超压立刻达到峰值,随后爆炸压强的数值指数形式衰减。与爆炸冲击的理论曲线趋势相对应,表明爆炸响应过程的可靠性。本节首先选取爆炸距离为50 cm,即编表5中工况为1进行分析。为更好的分析玻璃的裂纹响应,均采用应力云图反应玻璃的在爆炸冲击下的过程变化。
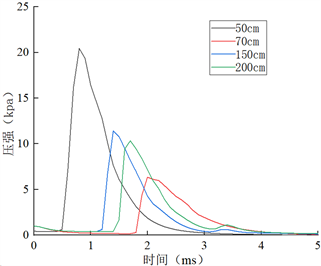
Figure 4. Course curves of the explosion shock wave with distance
图4. 爆炸冲击波随距离变化的历程曲线
图5表明了外层玻璃在爆炸冲击下不同时间的损伤云图。从图5中可以看出TNT爆炸后,经过0.1 ms,爆炸冲击波到达外层玻璃表面,玻璃中心出现局部压强,并且玻璃外层有向内侧凹陷的趋势,冲击波持续作用1 ms时,可以明显看出应力波不断地向四周传播,此时玻璃中心开始出现环状裂纹,并且玻璃外层内凹深度明显加深,达到2 ms时,应力波传播至整个外层玻璃,此时玻璃中心开始出现径向裂纹并且玻璃中心不断产生大量环状裂纹,经过4 ms后,由于环状裂纹与径向裂纹的影响,应力波不断向玻璃层对角方向传播,呈现出大量的鳞片状。随着时间的变化,爆炸压强开始持续衰弱,直到5 ms时,外层玻璃的裂纹形状保持不变,此时外层玻璃的响应过程基本结束。玻璃中心凹陷程度达到最大,裂纹深度更深。
图6表明了内层玻璃在爆炸冲击下不同时间的损伤云图。内层玻璃与外层玻璃观测角度相反,但与外层玻璃的损伤云图演化进程基本相似。从图6中可以看出,由于PVB层的影响,应力波传播至内层玻璃时,冲击能量略微减少,在3 ms前外层玻璃的损伤变化更加明显。但在拉伸反射波与外层玻璃不断向内侧凹陷的作用下,内层玻璃不断扩展裂纹深度,并最终产生的裂纹形状多余外层玻璃。
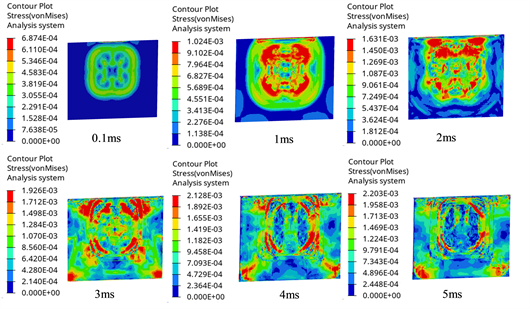
Figure 5. Damage cloud of outer glass
图5. 外层玻璃的损伤云图
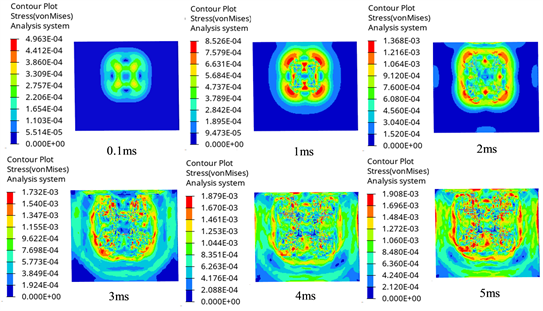
Figure 6. Damage cloud of inner glass
图6. 内层玻璃的损伤云图
图7表明了内层玻璃在爆炸冲击下不同时间的损伤云图。从图7可以看出,应力波在玻璃与PVB层的传播速度不同,由于PVB胶的超弹性特性,在受到剧烈的冲击下仍能保持良好的伸张性,应力波无法在胶层内瞬间反射,保证PVB胶层结构的完好,并且能黏住较多细小的玻璃碎渣,进一步减小玻璃在受到爆炸冲击后带来的安全隐患。因此PVB胶层在夹层玻璃结构中起到至关重要的作用。
TNT起爆后,夹层玻璃的结构响应随爆炸距离的变化产生不同的反应结果。图8表明了不同工况下外层玻璃最终的损伤云图。从图8(a)-(d)可以看出,当爆炸距离由50 cm至200 cm,夹层玻璃结构的损伤程度不断降低。在爆炸距离为70 cm时,玻璃夹层的结构响应出现一定的缓和,随爆炸距离的增长,最后只在外层玻璃上出现几条裂纹,玻璃较好的保存。此时,可以将爆炸距离150 cm定为安全距离。综合图8中四种工况的损伤云图,符合爆炸冲击下玻璃结构的动态响应,并且有效的验证了单元删除法的可行性。

Figure 8. Dynamic response of glass structure under different working conditions: (a) 50 cm; (b) 70 cm; (c) 150 cm; (d) 200 cm
图8. 不同工况下玻璃结构的动态响应:(a) 50 cm;(b) 70 cm;(c) 150 cm;(d) 200 cm
图9表明了不同爆炸距离下中心点Y向位移曲线图。从图9中可以看出,随爆炸距离的增加,玻璃中心点的响应时间有所迟滞,符合爆炸冲击的原理,并且位移曲线的斜率在逐渐变小。在50 cm时,中心点Y向位移达到7.64 cm,而在200 cm时,中心点的Y向位移仅有2.12 cm,因此爆炸距离对研究PVB夹层玻璃的影响尤为重要。
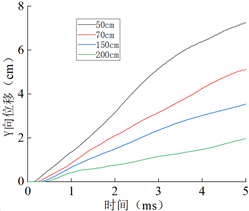
Figure 9. Y-direction displacement of the center point at different blast distances
图9. 不同爆炸距离下中心点Y向位移
PVB夹层玻璃中各个部件的吸能率可以反应爆炸响应的过程。图10给出了工况1中各个构件的能量吸收率。从图10可以看出,工况1下外层玻璃吸收了大部分的冲击能量,其次是内层玻璃,PVB胶层只吸收了一部分能量。由于爆炸冲击波直接作用在外层玻璃上,玻璃是脆性材料,易造成破碎,因为PVB胶层抵抗玻璃的形变,吸收一部分能量,传递到内层玻璃的能量降低,符合夹层玻璃在爆炸反应过程中能量吸收变化。
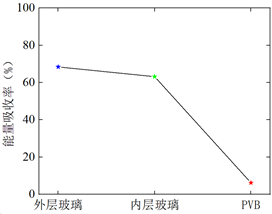
Figure 10. Energy absorption rate of PVB laminated glass components under case 1
图10. 工况1下PVB夹层玻璃各部件能量吸收率
4. 结论
本文研究了爆炸冲击下PVB夹层玻璃的动态响应,采用Hypermesh软件建立PVB夹层玻璃、空气域和TNT的有限元模型,通过Ls-Dyna软件模拟爆炸冲击过程,从损伤云图结果看,满足理论上玻璃裂纹扩展的趋势,验证了数值模拟的可靠性。并得到以下几点结论:
(1) 采用多物质流固耦合的方式建立爆炸有限元模型,并将爆炸冲击波曲线与理论曲线相比较,满足爆炸冲击波过程变化,验证了有限元模型的可靠性。
(2) 单层玻璃经爆炸冲击后,瞬间产生大量的飞溅碎片,而PVB夹层玻璃由于PVB胶的材料特性,在玻璃向内凹陷的过程中,吸收一部分能量,并有效吸附大部分玻璃碎渣,大大提升其安全性。
(3) PVB夹层玻璃各部分的损伤云图和能量吸收率可以看出,外层玻璃相较于内层玻璃吸收更多的能量,因为爆炸能量先作用于迎爆面,发生变形的时间略早于其他部件。但由于内层玻璃受到拉伸影响,最终产生的玻璃裂纹多余外层玻璃。