某汽车盘式制动器设计与热力耦合分析

Design and Thermal Coupling Analysis of a Certain Automobile Disc Brake

摘要: 本文通过将整车性能参数与盘式制动器设计有机结合，针对某汽车盘式制动器进行设计。首先通过选定同步附着系数以及计算在制动过程中汽车各个车轮的制动力和制动力矩，确定了盘式制动器的主要部件关键设计参数和材料，并经计算验证了制动器各项性能均符合相关法规要求。其次利用CAD软件对主要零部件进行三维建模和组装。最后利用有限元分析软件ABAQUS，建立该制动器热力耦合有限元模型，考虑制动时制动盘和摩擦片的热膨胀系数以及弹性模量随温度的变化，利用完全耦合方法，对盘式制动器的紧急制动工况进行仿真模拟，得到了该工况下制动盘温度场和应力场分布特性，并对两者之间的耦合关系进行分析，验证了本文盘式制动器设计的可行性。

Abstract: This paper integrates the overall vehicle performance parameters with the design of a disc brake system for a specific automobile. Initially, by selecting the synchronous adhesion coefficient and calculating the braking forces and moments for each wheel during the braking process, key design parameters and materials for the disc brake system were determined. The calculated results confirmed that the performance of the brake system complies with relevant regulations. Subsequently, major components were modeled and assembled in three dimensions using CAD software. Finally, employing finite element analysis software ABAQUS, a thermal-structural coupled finite element model of the brake system was established. This model considered the thermal expansion coefficients of the brake disc and friction pads, as well as the variation of elastic modulus with temperature during braking. Utilizing a fully coupled approach, the disc brake system was simulated under emergency braking conditions. The simulation yielded characteristics of temperature distribution and stress field for the brake disc under such conditions. An analysis of the coupling relationship between these factors was conducted, confirming the feasibility of the disc brake system design proposed in this study.

1. 引言

盘式制动器是现代汽车制动系统中的关键组件之一。它通过将制动力转化为热能，实现车辆的安全停车。盘式制动器由刹车盘和刹车卡钳两部分组成，其设计结构精巧，性能卓越。盘式制动器的设计以及热力耦合过程的研究对制动器合理设计开发、制动副摩擦材料研制与选择、制动盘的抗热疲劳、热衰退以及抗磨损性能等都具有重要作用。

国内外学者对盘式制动器的研究取得了显著成果。过振华 [1] 通过CAE方法分析某盘式制动器性能满足设计要求并通过实验验证了其有效性。苏旭武等人 [2] 结合多物理场对盘式制动器进行热力耦合分析并通过实验验证了其真实性。张雪松等人 [3] 针对盘式制动器制动噪声问题，通过复特征值法的有限元分析得到产生制动噪声的频率，而后通过制动试验验证了仿真结果的正确性。石康等人 [4] 考虑汽车连续制动和颠簸路段制动等工况对周盘式制动器进行热力耦合分析，台架试验数据验证了仿真结果的准确性。沈珺等人 [5] 为提高水冷盘式制动器的综合散热性能，采用CFD方法对制动器的流固耦合传热过程进行数值模拟，研究结果表明扰流柱顶部与静盘间距对综合散热性能的影响最为显著，并通过正交实验进行验证。

本文首先依据整车参数对制动器主要系数进行初步设计，选取合适的同步附着系数从而计算制动力和制动力矩。而后对设计的制动器参数进行性能校核以保证其符合设计要求，再通过三维建模软件UG进行绘图。最后利用有限元分析软件ABAQUS，建立该制动器热力耦合有限元模型，考虑制动时制动盘和摩擦片的摩擦系数以及弹性模量随温度的变化，利用完全耦合方法，对盘式制动器的紧急制动工况进行仿真模拟，得到了该工况下制动盘温度场和应力场分布特性，并对两者之间的耦合关系进行分析，验证了本文盘式制动器设计的可行性。

2. 盘式制动器设计

2.1. 同步附着系数与最大制动力矩计算

整车参数如表1所示。《汽车理论》一书中提到汽车在同步附着系数 ${\phi }_0$ 的道路上制动时，前后车轮会同时抱死，而此时它的制动减速度为 $d_{\mu }/d_t=qg={\phi }_{0}g$ ，也就是 $q={\phi }_0$ ，其中q为制动强度。这表明只有在 $\phi ={\phi }_0$ 的道路上制动时，道路的附着条件才能被充分利用。根据有关文献推荐轿车满载时候的同步附着系数应当不小于0.6；而货车满载的时候取不应该小于0.5。

根据《汽车理论》中对于同步附着系数的描述有：

$\frac{F_{f1}}{F_{f2}}=\frac{\beta }{1-\beta }=\frac{l_2+{\phi }_0{h}_g}{l_1-{\phi }_0{h}_g}$ (1)

化简得：

${\phi }_0=\frac{l\beta -l_2}{h_g}$ (2)

式中， $l_1$ 和 $l_2$ 分别为汽车质心到前轴和后桥的距离， $\beta$ 表示制动器制动力在前、后轴上的分配比例， $b$ 表示汽车的质心位置， $h_g$ 为汽车的质心高度。

代入上述整车性能参数计算确定同步附着系数 ${\phi }_0=\left(2960\times 0.7-1598\right)/570=0.83$ 。下一步要确定前轮制动器的制动力矩，假设衬块的摩擦表面与制动盘有很好的接触，且各个地方分布的压力均匀，则盘式制动器的制动力矩可以表示为：

$M_{\mu }=2fN{R}_m$ (3)

式中：N为单侧制动块对制动盘的压紧力；f为摩擦系数； $R_m$ 为制动盘平均半径。

此外，汽车的制动力矩还能由下式得到：

$M_{\mu max}=\frac{1}{2}{F}_{z1}\phi r$ (4)

式中：Fz1为满载时前轮的支反力，其值为 $1081\times 9.8=10593.8\text{N}$ ；φ为地面峰值附着系数，本文设计认为该车是在干燥沥青路面上行驶的情况，可以取 $\phi =0.7$ ；r为车轮的有效半径，根据文献车轮直径 = 车轮宽度 × 扁平率 × 2 + 轮辋直径 × 25.4，所以车轮有效半径为351.55 mm。

Table 1. Vehicle parameter table

表1. 整车参数表

要求制动器制动力矩要大于汽车的最大制动力矩才能有效制动，于是就有 $M_{\mu }\ge M_{\mu \max }$ ：

$M_{\mu }=2fN{R}_m\ge \frac{1}{2}{F}_{\text{z}1}\phi r$ (5)

带入数据即可得 $N\ge 14084.94\text{N}$ 。这就是所设计汽车所需的最小制动力。由于接下来要采用液压驱动机构，通过单侧制动块的压紧力就可得到轮缸最小直径：

$d_w=2\sqrt{\frac{F}{\pi p_0}}$ (6)

式中： $d_w$ 为轮缸直径；F就是N为单侧制动器的压紧力， $P_0$ 由汽车设计手册查得轿车压力管压力一般不超过10~12 MPa，盘式制动器可以高一些，取 $P_0=12\text{MPa}$ 。

代入数据到公式(6)可得 $d_w=38.66\text{mm}$ ，根据GB7524-87中选取标准尺寸为40 mm。再验算该轮缸直径下的制动力是否符合要求，具体公式如下：

$N=P_0{A}_W$ (7)

$A_W=\frac{\pi }{4}{d}_W^2$ (8)

联立式(7)和式(8)可得轮缸制动力为15079.56 N > 14084.94 N，满足设计要求。再将其代入式(3)可得盘式制动器的制动力矩为1393.36 Nm。

2.2. 盘式制动器结构参数与摩擦衬块系数的确定

制动盘直径D在通常情况下较大，这样有助于提高制动器的有效半径和降低制动钳的压力，只有压力降低了，制动时的温度才会下降。但是由于轮辋直径限制了制动盘的直径，制动盘直径就不能取得过大，它通常是轮辋直径的70%~79%，这里取轮辋直径的76%最为贴切真实数据。

轮胎的规格根据资料显示有两种，这里我们选取该车型标配版本的轮胎，具体参数为245/45 R19，显然根据轮胎国际标准，这里的轮辋直径为19英寸，即482.6 mm，故制动盘直径D = 482.6 × 76% = 366.776 mm，取365 mm。

制动盘的厚度h不仅影响其质量同时也是其工作时产生温度大小的关键，所以为了使质量减小，制动盘的厚度不宜取的太大，同时为了保证工作时的温度不太高，制动盘的厚度又不宜取得太小。为了散热通风，制动盘的中间可以加入散热孔道。本文设计的制动盘为通风盘式，而通风盘式的厚度大多取20~30 m，参考相关文献及实车数据，这里取28 mm较为合适。

参考合工大版《汽车设计》一书中的推荐要求，制动衬块的外半径和内半径的比值应该小于等于1.5，因为这个值过大会造成当汽车制动时，制动衬块内外的圆周速度有较大差距，就会导致磨损不均匀，从而使制动衬块和制动盘的接触面积减小，甚至会导致制动力矩变化大，严重影响汽车的安全性。这里取取 $R_2/R_1=1.4$ ，根据设计要求摩擦衬块外半径R₂应该略小于上文所取的制动盘半径 $D/2=182.5\text{mm}$ ，这里取180 m为宜。则根据比例关系 $R_1=180/1.4=128\text{mm}$ 。同时参考其他类似车型，选择厚度 $b=14\text{mm}$ 。

初步设计制动块是一个夹角为60˚的扇形，其工作面积根据数学公式可得：

$A=\pi \left(R_2^2-R_1^2\right)\times \frac{{60}^{\circ }}{{360}^{\circ }}=\pi \left({18.0}^2-{12.8}^2\right)\times \frac{60}{360}=83.86{\text{cm}}^2$ (9)

盘式制动器的结构形式决定了其制动效能比较低，对摩擦材料的要求较高，所以在选取摩擦材料时应该倾向于选择摩擦系数较高的材料，但同时此材料的散热也要好。根据图1所示各种制动器所使用的摩擦材料，它们的平均摩擦系数都维持在0.3~0.5之间。而且一般来说，材料的摩擦系数越高他的耐磨性相对而言就越差，这里初步选取粉末冶金材料。这里假设要在理想条件下计算制动器的制动力矩，为了方便计算取 $f=0.3$ 。

在制动衬块的设计计算中，制动衬块采用扇形摩擦表面，它的径向宽度不是很大，则可以取R等于平均半径 $R_m$ 或者有效半径 $R_e$ 。则制动衬块的平均半径 $R_m$ 为：

$R_m=\frac{R_1+R_2}{2}=\frac{128+180}{2}=154\text{mm}$ (10)

有效半径R_e是扇形表面的面积中心至制动盘中心的距离，如下式所示：

$R_e=\frac{2}{3}\times \frac{R_2^3-R_1^3}{R_2^2-R_1^2}=\frac{4}{3}\left[1-\frac{m}{{\left(1+m\right)}^2}\right]R_m=155.48\text{mm}$ (11)

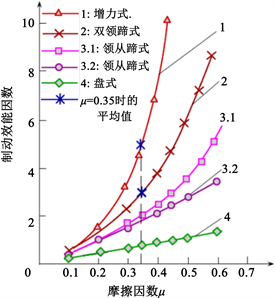
Figure 1. The relationship between braking efficiency factor and friction factor

图1. 制动效能因数与摩擦因数关系

有效半径 $R_e$ 与平均半径 $R_m$ 相差不大且满足 $m=R_1/R_2=128/180=0.71<1$ ，同时m的值也不应该小于0.65，这主要是因为如果m过小那么摩擦块上不同半径处的速度就会有很大差距。所以R取154 mm是完全符合要求的。

选取完摩擦衬块的半径后还需校核制动器的能量负荷，目前，各国常采用的作为评价能量负荷的指标是比能量耗散率，即单位时间衬块单位摩擦面积耗散的能量，通常所用的计算单位为W/mm²。本文所设计的盘式制动器的比能量耗散率为：

$e_1=\frac{\delta m_a\left(V_1^2-V_2^2\right)}{4t{A}_1}\beta$ (12)

式中， $m_a$ 为的整车质量；δ为汽车的旋转质量换算系数；V₁、V₂为制动初速度和末速度；t为制动时间；A₁为前制动器衬块的摩擦面积；β为制动力分配系数。

在紧急制动到停车的情况下， $V_2=0$ ，并可以认为 $\delta =1$ ，代入式(12)有：

$e_1=\frac{m_a{V}_1{}^2}{4t{A}_1}\beta$ (13)

根据有关文献的推荐，计算时取减速度j = 0.6 g，制动初速度V₁，乘用车用100 km/h (27.8 m/s)。而A₁ = 8386 mm²，代入得：

$t=\frac{V_1-V_2}{j}=\frac{27.8}{0.6\times 9.8}=4.73s$ (14)

联立式(13)易得本文所设计的盘式制动器的比能量耗散率 $e_1$ 为5.16 W/mm²，根据国家规定轿车盘式制动器的比能量耗散率应不大于6.0 W/mm²，故符合要求。

2.3. 式制动器主要零件结构设计

汽车制动盘一般由碳陶瓷制成，它的工作表面应该尽量保持光滑。综合上文考虑到制动盘高强度制动工况下温升速度不能太高而采用通风盘式。制动钳一般都是制作成两半，中间有螺栓连接，同时它的外缘应该留有开口这样即使不拆除制动钳也能更换制动块，非常方便。这种制动钳的强度和刚度都比较高而且还能防止振动。一般除了在制动钳的钳体中加工出制动油缸之外，还能单独制造油缸再镶嵌进钳体中。本文制动钳的制造选择的是前者，即液压油缸和制动钳体一体成型。至于活塞，一般做成杯型，它的开口一端紧压着制动块背板，一般都是用钢制成。

制动块主要由制动块和背板组成，他们可以通过挤压直接合成一体，本文就是采取的这种设计。衬块设计大都为扇形的结构，但也有矩形，长圆形的形式，有的活塞与制动块背板间加装消音片，活塞与制动快的接触面积应该应可能大，因为这样可以有效减小噪声。制动块背板由钢板制成，目前许多盘式制动器都配有电触点或者传感器，这样就可以在磨损到一定程度时向车内驾驶员报警，保证制动安全性。制动器的主要零件的三维模型画出之后，利用UG进行装配，其装配图如图2所示，其爆炸图如图3所示。

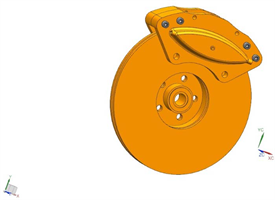
Figure 2. Disc brake assembly drawing

图2. 盘式制动器的装配图

Figure 3. Exploded view of a disc brake

图3. 盘式制动器的爆炸图

2.4. 盘式制动器主要零件静力学验证

静力学分析是研究物体在承受的所有力的情况下的平衡规律，它虽然没有动力学分析准确广泛，但也在研究中起着重要的作用。本文的静力学分析是用来计算盘式制动器在固定不变的压力和力矩下的响应，而所受到的响应是指制动器在在外力作用下产生的形变和应力应变。

如图4所示制动盘在最大制动力矩1393.4 N∙m，所受的最大应力为21.66 MPa，完全小于材料的屈服强度。因此该制动盘完全满足强度要求。其变形云图如图5所示。由变形云图可知，该制动盘在制动过程中的变形为0.0124 mm，也是在可接受的范围之内。

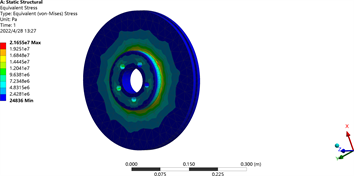
Figure 4. Brake disc equivalence force diagram

图4. 制动盘等效应力云图

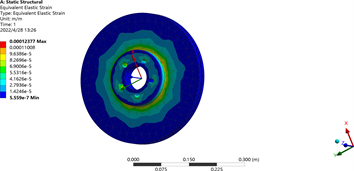
Figure 5. Brake disc deformation diagram

图5. 盘制动盘变形云图

为了方便仿真，本文仅用单个摩擦片进行受力分析，摩擦片的一面是受到来自液压轮缸的推力，另一面在制动时紧紧压住制动盘。其边界条件就较为简单，在摩擦片的一端施加由前文计算出来的单侧的压紧力15,080 N，另一端则为面约束。单侧摩擦片的应力云图和应变云图，见图6和图7。由云图可知单侧摩擦片的最大应力为41 MPa，其最大应力出现在摩擦片的边界倒角处，最大变形为0.02 mm也在可以接受的范围之内。

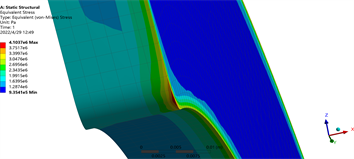
Figure 6. Friction plates equivalence force diagram

图6. 摩擦片等效应力云图

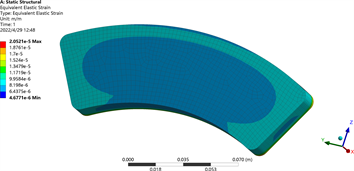
Figure 7. Friction plates deformation diagram

图7. 摩擦片变形云图

3. 盘式制动器热力耦合分析

3.1. 热力耦合分析理论模型建立

盘式制动器热力耦合理论模型的建立是有限元分析的基础。制动盘和摩擦片摩擦输入的热流密度满足：

$q\left(x,y,t\right)=\mu p\left(x,y,t\right)v\left(x,y,t\right)=\mu \frac{F\left(x,y,t\right)}{A}\cdot \omega \left(x,y,t\right)R_0$ (15)

式中， $q\left(x,y,t\right)$ 为摩擦输入的热流密度；μ为摩擦系数； $p\left(x,y,t\right)$ 为摩擦表面的比压； $v\left(x,y,t\right)$ 为制动盘和摩擦片的相对速度； $F\left(x,y,t\right)$ 为制动压力；A为制动盘与摩擦片的接触面积； $\omega \left(x,y,t\right)$ 为制动盘转动的角速度； $R_0$ 为制动盘和摩擦片接触的有效半径。

制动盘和制动器的热流分配系数η满足：

$\eta =\sqrt{\frac{{\rho }_d{c}_d{\lambda }_d}{{\rho }_p{c}_p{\lambda }_p}}$ (16)

式中， ${\rho }_d$ ， $c_d$ ， ${\lambda }_d$ 分别为制动盘的密度，比热容和热传导系数； ${\rho }_p$ ， $c_p$ ， ${\lambda }_p$ 分别为摩擦片的密度，比热容和热传导系数。

制动盘和摩擦片的三维瞬态温度场热传导方程为：

$\frac{\partial T}{\partial t}=\frac{\lambda }{\rho c}\left(\frac{{\partial }^{2}T}{\partial x^2}+\frac{{\partial }^{2}T}{\partial y^2}+\frac{{\partial }^{2}T}{\partial z^2}\right)$ (17)

式中，T为空间和时间的函数， $T=T\left(x,y,z,t\right)$ 。

为使得式(17)有唯一解，首先必须满足初始条件为制动盘和摩擦片在任意时刻和任意点的温度是已知的，即给定温度边界的单项值条件。其次假定制动盘和摩擦片边界变量的法向导数已知，即给定热流边界。最后还需要制动盘和摩擦片任意点、任意时刻的换热条件已知，即给定对流换热边界。

3.2. 热力耦合分析有限元模型建立

由于原始模型较为复杂，本文对原始模型进行简化以便更好的应用于有限元分析中，制动盘的热力耦合分析只需要保留制动盘和摩擦片即可，为了节省CPU算力，再对上述模型进行二次简化，简化模型如图8所示。

对摩擦衬块与制动盘模块分别划分网格。网格类型选择温度–移耦合，具有减缩积分与沙漏控制的网格单元C3D8RT。单元属于六面体8节点单元网格，具有三向线性位移，三向线性温度。整个模型包含单元数为16,837，节点数为45,869。考虑材料自身特性，本文所采用摩擦衬块的属性参数随温度变化而变化，具体属性如表2所示。

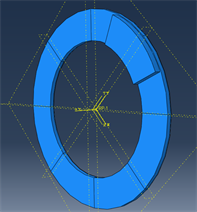
Figure 8. Simplified disc brake model

图8. 简化的盘式制动器模型

Table 2. Friction pad material properties

表2. 摩擦衬块材料属性

在紧急制动情况下，刹车的工况被设定为直到车的速度降为零。起始时，制动盘的角速对应的车速为60 km/h，转动惯量为30 Nm²，刹车压力设为1.7 MPa。热力耦合模型包括两个主要的边界条件：移动边界条件和热量边界条件。因摩擦片的位移仅沿制动盘的轴向发生，所以摩擦片受力的表面节点将其余两个方向的位移限制起来。由于制动盘只能朝着轴线方向转动，因此其他五个自由度被限定。选择面接触进行刚体约束并定义它们的相互作用。通过设定制动盘外表面以及摩擦片内表面接触区域的特性，热边界条件得以设定，热流的分配系数则通过公式计算后输入。最后设定初始温度为20℃。

3.3. 仿真结果分析

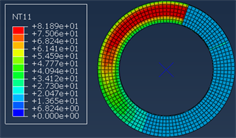
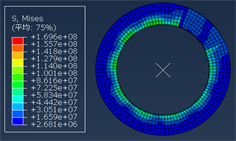
制动盘在制动过程中随温度变化明显，图9所示为本文所设计的盘式制动器制动时温度场云图。根据图9的云图显示，随着制动时间的延长，制动盘的温度逐渐升高。这是因为在制动初期，制动盘与摩擦块之间存在较大的相对速度，导致摩擦表面产生大量热量。在这个过程中，摩擦系数随着温度的上升而增加，同时摩擦片的弹性模量降低，形变量增大，从而导致制动盘的温度急剧上升。但温度很快会到达最大值，这是因为制动后期制动盘的转速下降，摩擦系数随着温度升高急剧减小，制动盘产生的热量一部分传递到空气中，导致制动后期制动盘的温度降低。由温度场云图还可以看出，制动盘的温度主要集中在制动盘中部区域，这是由于制动盘外侧与空气热交换较好，导致制动盘两侧温度较低。由图10可知制动盘所受应力变化也较为明显，随着制动时间的增加，摩擦衬块的摩擦系数随着温度的升高而不断变大，这就导致了制动盘所受应力不断增大。

盘式制动器热力耦合分析结果表明，本文所设计某汽车盘式制动器以整车安全性能为目标，从整车参数出发，其温度场和应力场分布符合实际情况，进一步验证了本文所设计盘式制动器的合理性。

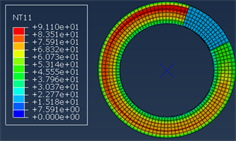
(a) (b)(c) (d)

Figure 9. Disc brake temperature field cloud diagram

图9. 盘式制动器温度场云图

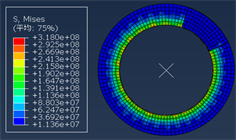
(a) (b)(c) (d)

Figure 10. Disc brake stress cloud diagram

图10. 盘式制动器应力云图

4. 结论

为达到整车安全性能的目标，我们致力于确定一种盘式制动器设计方案，并相应地推导出其制动器参数。在满足相关法规要求的基础上，简化了汽车制动器设计流程，通过静力学分析验证了本文所设计制动盘结构的合理性，并为进一步研究制动设计、热力耦合分析等问题奠定基础。

通过制动器热力耦合分析，我们发现在制动过程中，随着制动时间的延长，制动盘的温度逐渐升高，但温度很快会到达最大值，同时所受应力随着摩擦衬块的摩擦系数的升高而不断增大，摩擦片和制动盘形成了复杂的热力耦合机制。在制动过程中，应力场和温度场的变化趋势是相同的。特别是在制动时，摩擦片的弹性模量和制动器摩擦系数随温度的变化，对温度场和应力场的分布和变化规律产生重要影响。这些因素在制动器的仿真和实验中都是不容忽视的。