城市轨道交通网络关键节点识别与抗毁性分析

Identification of Key Nodes and Invulnerability Analysis of Urban Rail Transit Network

摘要: 如何准确高效识别关键节点和分析网络在突发事件下的抗毁性对于城市轨道交通网络的运行具有重要意义。首先，采用Space L方法构建城市轨道交通网络，定量分析网络的统计特性；然后，考虑到节点间的连接关系，以共同邻居节点数量定义接近度函数，并将接近度作为分配比例改进PageRank算法，使用改进算法识别网络的关键节点；最后建立级联失效模型，分析城市轨道交通网络在不同攻击方式下的抗毁性。以苏州轨道交通为例进行实证研究，结果表明：无论有无级联失效，苏州轨道交通网络面对随机攻击表现出较强的抗毁性，面对蓄意攻击时表现出脆弱性。同时，考虑级联失效的苏州轨道交通网络是更脆弱的。

Abstract: It is of great significance for the operation of urban rail transit network how to accurately and efficiently identify key nodes and analyze the network’s invulnerability under emergencies. Firstly, the Space L method is used to construct the urban rail transit network, and the statistical characteristics of the network are quantitatively analyzed. Then, considering the connection relationship between nodes, the proximity function is defined by the number of common neighbor nodes, and the proximity is used as the distribution ratio to improve PageRank algorithm. The improved algorithm is used to identify the key nodes of the network. Finally, a cascading failure model is established to analyze the invulnerability of urban rail transit network under different attack modes. The paper takes the Suzhou rail transit network as an example to make an empirical analysis. The results show that regardless of whether there is a cascading failure, Suzhou rail transit network shows strong resistance to random attacks and vulnerability to deliberate attacks. At the same time, in the case of cascading failure, Suzhou rail transit network is more fragile.

1. 引言

城市轨道交通具有高运输效率、高载客量、低碳排放等明显优势，已经成为了满足人们出行需求的重要方式。由于所处的位置和承担的负载，关键节点在城市轨道交通网络中发挥重要作用。一旦出现设备故障、自然灾害等突发事件，城市轨道交通的运行会受到影响，网络抗毁性迅速下降。因此，识别城市轨道交通网络的关键节点及分析网络的抗毁性对于保障城市居民的高效通勤和城市功能的持续运行具有重要意义。

现有文献对城市轨道交通进行了深入研究，研究视角由单层网络向多层网络发展。Zhang等 [1] 以网络效率和功能损失作为衡量指标对比分析了北京、广州、上海地铁网络面对蓄意攻击时的脆弱性。Wang等 [2] 研究了上海地铁网络在5种不同攻击场景下的脆弱性；蔡鉴明等 [3] 研究了长沙地铁网络的拓扑特性，对比分析了有无级联失效下网络的鲁棒性，结果表明无论有无级联失效，网络在蓄意攻击下较随机攻击更加脆弱。曲迎春等 [4] 构建城市公共交通双层网络，将出行失败率和出行时间增加率用于评估网络的脆弱性。Ma等 [5] 考虑客流的动态再分配，分析了公交-地铁双层网络面对随机攻击和蓄意攻击的鲁棒性。针对以往大多文献将城市轨道交通网络抽象为单层网络，没有充分考虑每条线路的差异性，Yin等 [6] 将每条城市轨道交通线路抽象为一层网络，建立多层有向加权网络。

现有研究多采用随机攻击和蓄意攻击2种方式分析城市轨道交通网络的抗毁性。蓄意攻击需要挖掘网络中的关键节点进行攻击。杨景峰等 [7] 以度中心性和介数中心性加权指标识别城市轨道交通网络的关键节点。蔡鉴明等 [3] 在度和介数基础上考虑客流量，结合度、介数、客流量三指标选取重要节点。焦柳丹等 [8] 把3类中心性指标、站点属性和客流中心性相结合，并采用变异系数法和VIKOR方法对节点进行排序。涂敏等 [9] 提出以基于余弦相似性的TOPSIS法评估节点重要度，一定程度上减少了逆序现象。由于PageRank算法不仅考虑节点自身因素，还考虑其他节点对本节点的影响，明玮 [10] 将其用于识别无权北京轨道交通网络的重要节点。沈型广 [11] 以客流量作为边权，将PageRank算法应用到加权网络中。

综上，现有城市轨道交通网络关键节点识别的研究大多基于度，介数等中心性指标和客流量指标。最初用于网页排序的PageRank算法 [12] 具有较高的准确性，本文将PageRank算法中PR值的分配调整为非平均分配，以改进算法识别关键节点，并分析城市轨道交通网络在不同攻击方式下的抗毁性。

2. 城市轨道交通网络拓扑特性分析

2.1. 城市轨道交通网络模型构建

城市轨道交通网络建模方法主要有Space L法、Space P法和Space R法三种。基于Space L方法建模时，需将站点抽象为节点，将两相邻站点间的线路抽象为连边，得到的网络与现实的城市轨道交通拓扑结构最为相似，所以本文采用Space L法构建城市轨道交通网络。

2.2. 城市轨道交通网络特征指标

城市轨道交通网络特征指标主要包括度、介数、聚类系数。各个指标含义及计算公式如表1所示。

Table 1. Main characteristic index of urban rail transit network

表1. 城市轨道交通网络主要特征指标

3. 城市轨道交通网络关键节点识别

3.1. PageRank算法

PageRank算法的核心思想有两点：一是入链数量越多，网页越重要；二是链接的网页质量越高，网页越重要。PageRank的计算公式如下：

$PR\left(v_i\right)=\frac{1-q}{N}+q{\displaystyle \underset{v_j\in M(v_i)}{\sum }\frac{PR\left(v_j\right)}{L\left(v_j\right)}}$ (1)

式中， $PR\left(v_i\right)$ 表示节点 $v_i$ 的PageRank值， $L\left(v_j\right)$ 表示节点 $v_j$ 的出链数量， $M\left(v_i\right)$ 表示节点 $v_i$ 的入链构成的集合， $N$ 表示网络中节点的总数， $q$ 为阻尼系数，一般 $q=0.85$ 。

3.2. 改进算法

3.2.1. 算法原理

传统PageRank算法在进行PR值分配时采取的是平均分配的思想，但考虑到节点间的连接关系，且拥有共同邻居节点数量越多的两个节点关系越紧密，本文以共同邻居节点数量定义了接近度函数，接近度函数的计算如(2)所示。同时将接近度作为分配比例，提出了一种改进的PageRank算法。改进PageRank的计算公式如(3)所示。

$ne{i}_{ij}=\{\begin{array}{l}\left|d\left(i\right)\cap d\left(j\right)\right|+1,a_{ij}\ne 0\\ 0,a_{ij}=0\end{array}$ (2)

(3)

式中， $ne{i}_{ij}$ 表示节点 $i$ 和节点 $j$ 间的接近度， $d\left(i\right)$ 表示节点 $i$ 的邻居节点构成的集合， $d\left(i\right)\cap d\left(j\right)$ 表示节点 $i$ 和节点 $j$ 的共同邻居节点构成的集合， $O\left(v_j\right)$ 表示节点 $v_j$ 的出链构成的集合。

从式(3)可以看出：1) PR值的分配不再是平均分配，而是与节点间的接近度有关；2) 节点与相邻节点间的接近度越大，计算得到的PR值越大，说明节点越重要；3) 相邻节点越重要，该节点就越重要。

3.2.2. 算法步骤

1) 根据网络图生成邻接矩阵 $M={\left(a_{ij}\right)}_{N\times N}$ 。若存在由节点 $i$ 到节点 $j$ 的链接，则 $a_{ij}=1$ ，否则 $a_{ij}=0$ 。

2) 根据公式计算接近度，得到矩阵 $P={\left(ne{i}_{ij}\right)}_{N\times N}$ 。

3) 计算矩阵 $P$ 的行和 $r_i$ 。

$r_i\text{=}{\displaystyle \underset{j}{\sum }ne{i}_{ij}}$ (4)

4) 定义矩阵 $S$ 为矩阵 $P$ 的每个元素除以所在行的行和，将矩阵 $S$ 进行转置，得到 $S^{\prime }$ 。

$S=\left(\frac{ne{i}_{ij}}{r_i}\right)$ (5)

5) 赋给节点初始PR值，均为 $\frac{1}{N}$ 。

6) 根据公式更新各节点的PR值。

$R_{t+1}=q{S}^{\prime }{R}_t+\frac{1-q}{N}I$ (6)

$R_t=\left(\begin{array}{l}P{R}_t\left(v_1\right)\\ P{R}_t\left(v_2\right)\\ \begin{array}{ccc}& ⋮& \end{array}\\ P{R}_t\left(v_N\right)\end{array}\right)$ (7)

式中， $R_t$ 为第t次迭代由各节点的PR值组成的向量， $I$ 为元素均为1的 $n\times 1$ 阶矩阵。

7) 当连续两次计算值的距离小于设定阈值 $e\left(e={10}^{-6}\right)$ ，即 $\Vert R_{t+1}-R_t\Vert <e$ 时，结束算法。

4. 级联失效模型

网络中的一个节点失效后，会通过连边影响其他节点，导致更多节点失效，使得失效在网络中传播。级联失效一旦发生，就会对网络造成严重后果，影响人们的生活。本文采用负载–容量模型 [13] 研究苏州轨道交通网络的级联失效问题。

4.1. 初始负载

Wang等 [14] 认为节点的初始负载不仅和节点的度有关，还和相邻节点的度有关。网络中节点 $i$ 的初始负载可用式(8)计算：

$L_i\left(0\right)={\left(k_i{\displaystyle \underset{m\in {\delta }_i}{\sum }{k}_m}\right)}^{\alpha }$ (8)

式中， $k_i$ 表示节点 $i$ 的度， ${\delta }_i$ 是节点 $i$ 的邻居节点构成的集合， $\alpha$ 是负载参数。

4.2. 容量

作为节点可承担的最大负载量，由于成本的限制，容量不可能是无限的。在Motter-Lai模型 [15] 中，容量和初始负载间存在线性关系，则节点 $i$ 的容量可用式(9)表示：

$C_i=\left(1+\beta \right)L_i\left(0\right)$ (9)

式中， $L_i\left(0\right)$ 表示节点 $i$ 的初始负载， $\beta$ 是容忍参数， $\beta >0$ 。

4.3. 负载重分配规则

网络中节点的状态有“正常”和“失效”两种。受攻击节点、负载大于容量的节点和孤立节点均属于失效节点，反之则为正常节点。在节点失效后，需要按照负载重分配规则将失效节点的负载分配给其他正常节点。本文以实时剩余容量策略作为负载重分配的规则。一般地，节点的剩余容量越大，可接受的负载越多。 $t$ 时刻节点 $j$ 的剩余容量计算公式如(10)所示：

$S_j\left(t\right)=C_j-L_j\left(t\right)$ (10)

式中， $C_j$ 表示节点 $j$ 的容量， $L_j\left(t\right)$ 表示 $t$ 时刻节点 $j$ 的负载。

当节点 $i$ 失效时，它的正常邻居节点 $j$ 获得的额外负载如(11)所示：

$\Delta L_j=L_i\left(t\right)\frac{S_j\left(t\right)}{{\displaystyle \underset{d\in {\delta }_i}{\sum }{S}_d\left(t\right)}}$ (11)

式中， $\Delta L_j$ 表示节点 $j$ 接受的额外负载， $L_i\left(t\right)$ 表示 $t$ 时刻节点 $i$ 的负载， $S_j\left(t\right)$ 表示 $t$ 时刻节点 $j$ 的剩余容量。

完成负载重分配后，节点 $j$ 的负载变为：

$L_j\left(t+1\right)=L_j\left(t\right)+\Delta L_j$ (12)

如果 $L_j\left(t+1\right)>C_j$ ，则节点 $j$ 失效，开始新一轮的负载重分配过程；如果 $L_j\left(t+1\right)\le C_j$ ，则节点 $j$ 不失效，级联失效过程结束。

5. 实例分析

苏州是中国内地第十五个开通城市轨道交通的城市，同时也是首个开通城市轨道交通的地级市。根据《苏州市城市轨道交通第三期建设规划调整(2021~2026年)》，本文将苏州市2026年规划后的9条轨道交通线路作为研究对象，利用Space L法构建城市轨道交通网络。在构建城市轨道交通网络时，做出以下规定：

1) 不考虑方向、客流量等因素，本文研究的是无向无权网络。

2) 不考虑两站点间线路的实际形状和距离，均抽象为一条边。

3) 2号线和6号线均经过金尚路至桑田岛这一区间，在计算度时对这2个站点都增加了一个度值。

5.1. 苏州轨道交通网络拓扑特性分析

表2为苏州轨道交通网络拓扑特性指标。苏州轨道交通网络由251个站点和283条边构成，平均度为2.26，说明平均一个站点有2个邻居站点；平均最短路径长度为16.57，网络直径为59，即网络中任意两节点间距离最大为59，网络效率较低。

Table 2. Characteristic index of Suzhou rail transit network

表2. 苏州轨道交通网络特征指标

图1所示为苏州轨道交通网络站点度分布及累计度分布。网络中站点度的范围为[1, 4]，其中度值为1、2、3、4的站点分别有12、199、2、38个。网络中度值为2的站点占比最大，为79.28%；度值为3的站点占比最小，为0.8%。网络中超过80%的站点度值不大于2，即苏州轨道交通网络中换乘站的数量较少。将度值大于等于3的站点称为大度站点，则大度站点共有40个，主要分布在2号线和3号线。

Figure 1. Distribution of degree and cumulative degree

图1. 站点度分布及累计度分布

图2所示为苏州轨道交通网络累计度分布的拟合结果。若利用幂律分布进行拟合，拟合函数为 $f\left(k\right)=1.085\times k^{-0.9456}$ ， $R^2=0.661$ ；若利用指数分布进行拟合，拟合函数为 $f\left(k\right)=1.886\times e^{-0.5411k}$ ， $R^2=0.7672$ ；若利用高斯分布进行拟合，拟合函数为 $f\left(k\right)=1.197\times e^{{}^{-{((k-1.1468)/1.105)}^2}}$ ， $R^2=0.9684$ 。通过比较 $R^{\text{2}}$ 的值可知，高斯分布的拟合效果较好，即该网络不具有无标度特征。

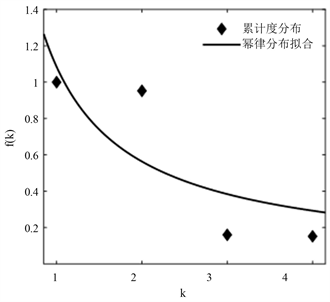
(a) 幂律分布拟合曲线

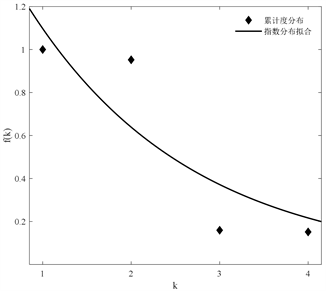(b) 指数分布拟合曲线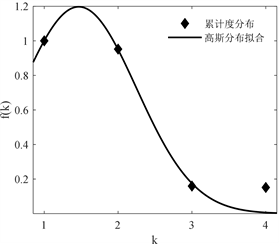(c) 高斯分布拟合曲线

Figure 2. Fitting curve of cumulative degree distribution

图2. 累计度分布拟合曲线

表3为苏州轨道交通网络节点介数分布情况。网络中节点介数最小为0，12个介数为0的节点均为线路的首末站；节点介数最大为0.2531，即：李公堤西，位于3号线和6号线的交叉处。超过80%的节点介数小于0.1，仅有3个节点介数大于0.2，网络中高介数值的站点数量较少。

网络中仅有3个站点聚类系数非0，即平河路站、苏州火车站、苏锦站，这三个站点的聚类系数均为0.1667，且三站点间两两连通，构成了三角形结构。

5.2. 苏州轨道交通网络重要站点

根据改进PageRank算法，计算苏州轨道交通网络各站点的重要性值，表4列出了前20个重要站点。

由表4可知：

1) 排名前二十的车站度均大于2，即都为换乘站，说明一般在网络中换乘站比普通站点更重要。其中，最重要的站点是苏锦站，位于4号线和6号线的交叉处。

Table 3. Distribution of betweenness

表3. 节点介数分布

Table 4. Top 20 stations of Suzhou rail transit network in importance order

表4. 苏州轨道交通网络排名前20站点

2) 排名前二十的车站介数均大于0.05，其中，有5个车站的介数大于0.15，占比25%；介数大于0.1的车站有13个，约占65%，说明改进算法识别的关键站点一般是高介数值的站点。

3) 排名前七的站点中，有4个站点位于2号线，分别为：平河路站、苏州火车站、松涛街站、高铁苏州北站，说明2号线是网络中的关键线路。2号线建设时间早，线路共设有39个站点，其中，有12个换乘站，与1号线，3号线等多条线路连通。此外，3号线和8号线构成“组合环线”，极大方便了居民出行。

5.3. 抗毁性分析

5.3.1. 抗毁性评价指标

1) 网络效率：将两节点间的效率定义为两节点间距离的倒数，计算公式为：

$E=\frac{1}{N\left(N-1\right)}{\displaystyle \underset{i\ne j}{\sum }\frac{1}{d_{ij}}}$ (13)

式中， $d_{ij}$ 表示节点 $i$ 和节点 $j$ 间的距离， $N$ 为网络节点总数。

2) 最大连通子图相对大小：攻击结束后网络中最大连通子图所含节点数与初始网络中节点数之比。计算公式为：

$G=\frac{N^{\prime }}{N}$ (14)

式中， $N$ 表示初始网络中节点的总数， $N^{\prime }$ 为攻击结束后最大连通子图所含节点数。

5.3.2. 攻击策略

采用随机攻击和蓄意攻击两种方式来模拟网络遭遇突发事件的情况。随机攻击是指随机地选取网络中的节点进行攻击，在城市轨道交通网络中对应网络的站点遭受设备故障、自然灾害等偶发事件；蓄意攻击是指按节点重要性从高到低攻击节点，在城市轨道交通网络中对应网络遭受恐怖袭击等针对性事件。其中，蓄意攻击分为三种，即度值攻击、介数攻击和重要度攻击。在实验中，负载参数 $\alpha$ 设为1，容忍参数 $\beta$ 设为1.4。

图3为不同攻击方式下的网络效率变化情况。与级联失效相比，同一攻击在非级联失效下对应的网络效率曲线更平缓，表明若不考虑级联失效情况，网络的抗毁性更强。其中，在非级联失效场景，随机攻击、度值攻击、介数攻击和重要度攻击下，分别移除网络中的30、10、22、12个节点，网络效率均约为初始时刻的50%。在级联失效场景，随机攻击50个节点后，网络效率下降83.45%。度值攻击、介数攻击和重要度攻击下，分别移除网络中的5、18、3个节点，网络效率均约为0。即：不管有无级联失效，随机攻击下网络的抗毁性最强，基于度值和重要度的攻击方式是更具破坏力的。

Figure 3. Network efficiency values under different attack modes

图3. 不同攻击方式下的网络效率值

图4为不同攻击方式下的最大连通子图相对大小变化情况。非级联失效随机攻击曲线的下降速度略小于级联失效随机攻击曲线。级联失效下，三种蓄意攻击方式对应的最大连通子图相对大小曲线存在骤降现象。采用度值攻击时，仅移除5个节点，最大连通子图相对大小降至1.59%；采用介数攻击时，仅移除18个节点，最大连通子图相对大小降至0.8%；采用重要度攻击时，仅移除3个节点，最大连通子图相对大小降至0.4%。在经历骤降后，曲线逐渐平稳。

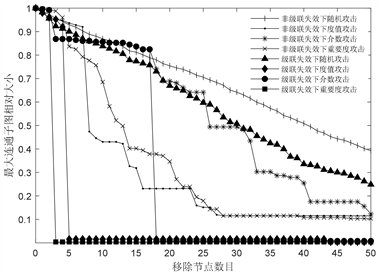
Figure 4. Relative size of largest connected subgraph ratio under different attack modes

图4. 不同攻击方式下的最大连通子图相对大小值

6. 结论

本文基于复杂网络理论，采用Space L方法构建苏州轨道交通网络；基于非平均分配的思想，改进PageRank算法以识别网络的关键节点，建立了级联失效模型，分析网络在突发事件下的抗毁性。结果表明：

1) 苏州轨道交通网络的累计度分布服从高斯分布，即该网络不具有无标度特征。

2) 利用改进PageRank算法识别的关键站点一般是度值和介数较大的节点。苏州轨道交通网络中最重要的站点是苏锦站，关键线路为2号线。

3) 无论有无级联失效，与蓄意攻击相比，苏州轨道交通网络在随机攻击下的抗毁性更强。若不考虑级联失效，苏州轨道交通网络的脆弱性被低估。

4) 本文构建的是无向无权网络，未考虑客流量等因素对网络的影响，未来应加入多种因素进行深入研究。

NOTES

^*通讯作者。