1. 引言
光子晶体(Photonic Crystals, PC)是一种具有周期性结构的材料,其提出与发展源自1987年由S. John [1] 和Eli Yablonovitch [2] 分别独立提出的理论概念。光子晶体的周期性结构可以在一定波长范围内产生光子带隙,类似于电子在原子中的禁带,阻止特定波长的光传播,形成光子禁带 [3] ,即当电磁波落在光子带隙内时将不能继续传播下去。这种材料革命性地改变了光学领域,允许人们通过在光学材料中引入周期性的折射率变化来控制光的传播。这一特性为光学材料和器件设计带来了前所未有的自由度。随后C Luo等研究人员发现了二维光子晶体具有负折射效应,并在此基础上深入研究,揭示了光子晶体具有亚波长聚焦能力 [4] 。此外,光子晶体还展现出一系列引人注目的特性,包括成像特性 [5] [6] 、成像测量 [7] [8] 、可调谐光束 [9] 、以及自准直效应 [10] 。借助这些特性,人们成功设计出了多种创新的光学元件,如超棱镜 [11] [12] 和光子晶体波导 [13] [14] ,为光学领域带来了重要的突破和应用前景。
而在2005年,梯度光子晶体的概念由David Cassagne和Emmanuel Centeno共同提出,梯度折射率光子晶体(Gradient Index Photonic Crystals, GIPC)是一种特殊的光子晶体结构,与传统的均匀谐振光子晶体不同,其主要特点是通过改变某些PC参数,例如晶格常数,使得光子晶体折射率在空间中平滑变化,创造了一种独特的光学环境,为特定范围内控制电磁波的传播提供了新的思路与工具。随着进一步的研究与探索,人们发现了GIPC的更多应用领域,例如A. E. Schedl利用衬底的局部应变改变反射率梯度使得复杂反射率颜色图案的可调谐形成 [15] 。Z Zhu发现梯度折射率光子晶体可以很好地改善由于晶体厚度增加而引起的光输出的急剧下降问题 [16] 。而X. Huang [17] ,Y. Huang [18] 等人的研究分别在光子晶体的不同方向上设置了梯度渐变折射率,实现了可变焦的亚波长聚焦效果。例如在X. Huang的研究中对光子晶体在纵向上设置了等效折射率梯度变化,设计了一种梯度负折射率光子平板透镜实现了焦点FWHM值为0.36 λ的聚焦效果,然后利用油浸技术将焦点FWHM值缩小到0.34 λ。而Liang [19] 等人提出了一种具有突破性的GEM平板透镜,通过横向的负折射率梯度设计,该透镜能够克服物体距离的限制,成功实现了在最大物距为50 μm时的亚波长聚焦成像。
除此之外,在亚波长聚焦方面,利用介质微球来突破衍射极限是非常简洁高效的方法之一 [20] [21] ,许多的研究表明,透明材质的电介质微球能够在亚极限尺寸内实现成像聚焦,并且这种微球还可以形成光子射流,将光聚集在光子束中,具有非常良好的超分辨能力。例如2010年Zengbo Wang [22] 使用直径2 μm的玻璃微球做光学显微镜以用来观察病毒,最好分辨率可达到λ/8。证实了微球是一种高性能光学超透镜。
本文依然针对梯度折射率光子晶体的亚波长聚焦展开研究,提出了一种双向梯度折射率变化的光子晶体亚波长聚焦研究,并在此基础上与硅微球组成可调控的变焦系统,针对其亚波长聚焦特性展开研究。整体模型的基底材料为硅,折射率为3.45。介质柱为圆形空气孔设计楔形光子晶体,运用平面波展开(PWE)方法分析能带图和二维时域有限差分(FDTD)方法仿真光在光子晶体中的传播路径,探究空气孔直径与梯度折射率光子晶体等效折射率的关系,并设计出一种双向梯度负折射率的光子晶体模型,通过横向和纵向调整光子晶体中折射率的特定分布,焦点的半峰全宽值减小到了0.341 λ,并基于此模型提出了一种双向梯度负折射光子晶体和单个硅透镜相结合的亚波长聚焦系统,通过硅透镜曲率优化,位置改变,带动第一次聚焦到硅透镜上的焦点移动,从而使得最终图像的像点半峰宽度、位置都发生改变,并且突破衍射极限在远场实现亚波长分辨率的超聚焦,此系统在0.13 λ~0.76 λ的亚波长下成像可调谐范围,并且焦点处最小半宽值为0.288 λ。相较于X. Huang [17] 的单一方向梯度折射率渐变模型最佳结果的0.34 λ左右,有了良好的优化效果。
2. 模型设计与原理
本文使用的二维空气柱型光子晶体是由硅(n = 3.42)为基底的,圆形介质柱为空气(折射率为1),晶格常数为a = 482 nm,并成正六边形排列。空气孔初始直径设为D = 0.831a,选用1550 nm的入射波长。并在光子晶体的上斜面边缘加设光栅参数为w1 = 0.71a,w2 = 0.78a,h1 = 0.513a,h2 = 0.963a,周期为a的等周期防反光栅 [23] ,像点与出射楔面的垂直距离为d,而硅透镜出射面与楔形光子晶体下表面距离为
。具体结构设计如图1所示。
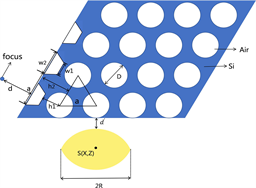
Figure 1. Schematic diagram of basic variables for two-dimensional air column photonic crystals and silicon lenses
图1. 二维空气柱型光子晶体与硅透镜基础变量示意图
在研究光子晶体中的负折射效应和亚波长聚焦时,普遍会使用光子带结构和等频图的分析方法。首先,在光子晶体折射率均匀并且空气孔直径为0.831*a时的情况下,本文使用Rsoft CAD中的BandSLOVE模块(基于平面波展开法,PWEM)对光子晶体进行数值模拟分析,得到了光子晶体的第一能带的等频图,图中,Kx和Ky分别表示波矢K在X和Y方向上的分量。
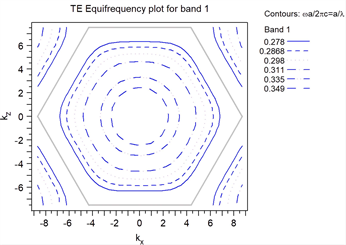
Figure 2. Iso-frequency diagram of TE polarized light in the first photonic band gap of a photonic crystal
图2. TE偏振光在光子晶体第一光子带隙等频图
由图2可明显看出,等频面呈环形,光子晶体表现为各向同性,等频线最内侧至最外侧的趋势是逐渐减小,TE波在光子晶体中的第一光子带隙中,群速度和相速度相反,波矢K和坡印廷矢量S的点乘为负,表明了此种光子晶体中存在负折射现象。此外当波长λ = 1550 nm时,对应的归一化角频率w0 = a⁄λ= 0.311。从图2中可得出此时波矢
。根据公式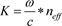 和
,可以得到当空气孔柱直径D = 0.831*a时,其光子晶体的等效折射率
= −1.184。
和
,可以得到当空气孔柱直径D = 0.831*a时,其光子晶体的等效折射率
= −1.184。
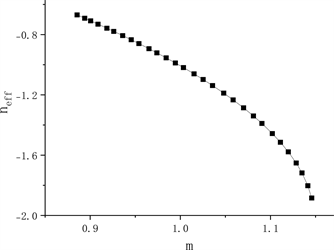
Figure 3. The relationship between the variation factor m of air hole size and the equivalent refractive index
图3. 空气孔大小变化倍数m与等效折射率的关系
研究结果指出,当等效折射率接近−1时,光子晶体表现出亚波长的聚焦特性。故经过Rsoft数值模拟,连续改变光子晶体的空气柱直径,便可以测算出特定等效折射率n范围内的基于硅基底的空气孔型光子晶体空气孔直径D数值。令
然后用matlab拟合,最终得到m与n两者关系式m = −0.1424n2 − 0.5778n + 0.5626。如图3(a)所示,可以明显从图中得到,变化后的空气孔直径
相对于空气孔直径D的倍数m与等效折射率n成反比关系,当m为0.9567即变化后空气孔直径
为0.795*a时,等效折射率恰好为−1。
电磁波在内部折射率分布模式不均匀的楔形二维光子晶体内传播时,会出现难以预测的焦移现象。本文充分利用这一现象,通过逐渐改变优化内部结构,尤其是根据先前实验得到的空气孔直径变化倍数m与等效折射率n的反比关系。我们设计了纵向上的空气孔直径梯度变化和横向上的空气孔直径梯度变化相结合的方案。可以合理预期,在特定模式下将产生一定的焦移补偿,使得光线在光子晶体中连续偏移,最终聚焦到一点,实现更高分辨率的聚焦效果。并且根据实验组之前的实验 [23] ,本研究在楔形光子晶体表面引入了等周期的亚波长光栅结构。该结构的设计旨在强化高空间频率分量的耦合效应,同时引入新的电场分量以实现像点的FWHM减小。基于等效介质理论的考虑,这一结构等效于一层增透薄膜,从而有效地提高光的能量透过率。如图4所示,是硅微球与双向梯度负折射率楔形光子晶体相结合的折射率分布模式示意图。

Figure 4. Biaxial gradient refractive index distribution mode schematic diagram
图4. 双向梯度折射率分布模式示意图
本文设定了从左往右的7列60˚倾斜的空气孔直径大小形成梯度变化,分别为C1~C7,其代表在横向上的每一列60˚倾斜的空气孔直径的变化倍数为m1。而9行从下到上的空气孔分别为L1~L9,纵向每一行的空气孔直径的变化倍数为m2,最终双向梯度变化的空气孔直径
。通过m1与m2的变化相结合,形成特定的折射率分布模式,从而产生一定量的焦移补偿。如表1,列出了本文设计双向梯度负折射率分布模式的m1与m2值。

Table 1. Bidirectional gradient negative refractive index distribution pattern
表1. 双向梯度负折射率分布模式
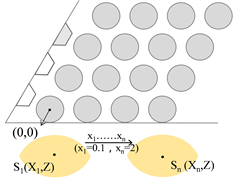
此外,为了方便后续实验进行,并可以与优化结果参照,所以基础空气孔直径设置为等效折射率为−1的时候即D = 0.795*a。同时,硅球几何中心位置点S坐标设为(X, Z),楔形光子晶体左下角第L1行,C1列空气孔中心点设为A(0, 0),并且硅透镜出射面与光子晶体下表面距离为
。随后,通过改变X与
的数值大小,控制硅透镜的空间位置变化,以探究硅透镜的位置变化是否可以对系统成像性能产生影响和它们之间的关系。
3. 模型仿真与结果讨论
本文使用RsoftCAD软件里的FullWAVE模块来模拟成像过程,其中理想匹配层(PML)厚度设置为 0.5 µm,网格精度收敛为0.02 µm,硅透镜初始前后面曲率半径都设为1.1*R,宽度为2R(R = 3*a),在硅透镜的z轴底部一侧设置波长为1550 nm,能量为 1 a.u.的平行光束,光源宽度与硅球宽度皆为2R。鉴于倏逝波随传播距离呈指数衰减的特性,本文将硅透镜初始中心S的z轴方向坐标设置在楔形光子晶体下表面0.4 μm处的近场区域,同时x轴位置设定为X = 1。这样的设置旨在确保经过硅透镜聚焦后的像点位置位于近场,以最大程度地减缓倏逝波衰减的速度。
在表1所示的特定折射率分布模式下,初始条件不变,硅透镜放置在距光子晶体下侧垂直距离0.4 μm,此时像点处的半峰全宽值为0.341 λ,其光线传播图如图5所示。从实验结果可以观察到,当平行光线经过硅透镜汇聚后,其焦点正好位于硅透镜的后表面。此时,光线通过光子晶体发生二次折射,然后汇聚在楔形梯度负折射率光子晶体的斜面上。值得注意的是,所实现的聚焦半宽度小于半个波长,从而实现了亚波长的聚焦效果。这一结果清晰地表明了双向梯度负折射率分布模式的有效性。
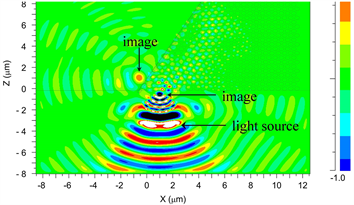
Figure 5. Imaging diagram with
of 0.04 μm
图5.
为0.04 μm时的成像图
在探究硅透镜空间位置对系统性能的影响之前,首要任务是对硅透镜的曲率进行优化。旨在研究经过不同曲率半径的硅透镜后形成的光斑最终对整体系统成像性能的影响,为后续实验的顺利进行提供基础。所以本文设置了不同曲率半径CR = C*R,在其他实验条件不变的情况下进行试验,C实验范围为1.02~1.2。最终得到仿真数据,如图6所示,可以看出,当曲率CR为1.13*R时像点的FWHM值最低,效果最好。故后续实验中硅透镜的曲率半径就设定为1.13*R。

Figure 6. Relationship between radius of curvature and imaging performance of image points
图6. 曲率半径与像点成像性能的关系
根据Huang [17] ,Lei [23] 研究表明点源位置的变化会直接影响成像时数值孔径角的尺寸,从而对最终图像的像点半峰宽度、强度和位置产生影响。而硅透镜聚焦后的效果与点源相似,所以也要研究硅透镜的位置是否会直接影响最终图像的像点半峰宽度等成像性能。在图1中,微硅透镜出射面到光子晶体下边缘的垂直距离为
。经过之前实验,硅透镜曲率半径设置为1.13*R (R = 3*a),此曲率下的硅透镜的聚焦效果最好,并在光源经过硅透镜聚焦后恰好聚焦在出射面,形成极小的光斑。为避免光斑进入光子晶体内部,预留了一定的间隔在硅透镜与光子晶体下表面之间。
在之前系统参数保持不变的情况下,仅通过调整
,经过Rsoft仿真探测器监测了
在0.1到1.6µm范围内移动时最终成像的光斑大小和像点运动轨迹,并研究了其对于焦点成像性能的影响,如图7(a)、图7(b)所示。

 (a) (b)
(a) (b)
Figure 7. (a) Focus and final imaging focus path of the silicon lens exit surface under longitudinal movement; (b) The impact of changes in  on focal imaging performance
on focal imaging performance
图7. (a) 纵向移动下硅透镜出射面的焦点和最终成像焦点路径;(b)
的改变对于焦点成像性能的影响
由之前的实验结果可知,在X = 1 µm,
= 0.4 µm时,最优半宽结果为0.322 λ,而经过实验发现,在
= 0.3 µm时结果最好,仅有0.298 λ,但再缩小
后,也许是光斑进入了光子晶体内部,导致半宽增加,并且随着
的逐渐增大,成像焦点像距逐渐增大,开始远离出射面,在归一化像距为0.76 λ时,半宽仍属于亚波长成像范围。
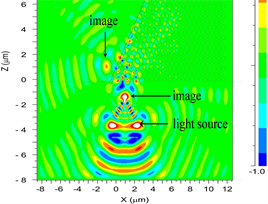
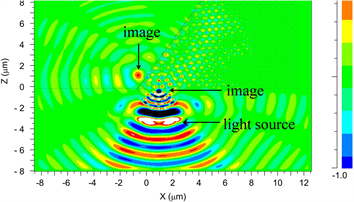
为0.3 µm和1.6 µm时的光路图如图8(a)、图8(b)所示。
 (a) (b)
(a) (b)
Figure 8. (a) The optical path diagram when the exit surface of the silicon lens is
= 0.3 μm from the lower surface of the photonic crystal; (b) The optical path diagram when the exit surface of the silicon lens is
= 1.6 μm from the lower surface of the photonic crystal
图8. (a) 硅透镜出射面与光子晶体下表面
为0.3 μm时的光路图;(b) 硅透镜出射面与光子晶体下表面
为1.6 μm时的光路图
同理,在本文也监测了X在0.1~1.6 µm时的的成像效果,硅透镜位置按照图9(a)移动轨迹所示移动,最终得到了相关的仿真数据如图9(b)、图9(c)所示。
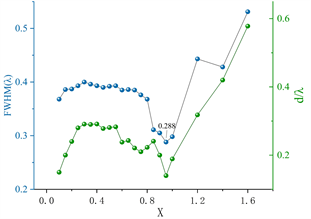
而根据图9(b)可知,当X为0.95 µm时,像点的全峰半宽最低为0.288 λ,并且硅透镜在0.1~1.4 µm范围内移动时始终保持着亚波长聚焦,实验结果表明,在像点位置,半宽度显著减小的同时,相应的像距也随之减小。这为未来研究提供了一个参考,可根据对实际输出位置和半宽等具体需要进行取舍,为应用奠定了基础。
4. 总结与讨论
本研究提出了一种基于双向梯度负折射光子晶体和单个硅透镜的亚波长聚焦系统,旨在突破衍射极限,在远场实现亚波长分辨率的超聚焦。实验中采用硅介质作为光子晶体基底和微球透镜,其折射率为
 (a)
(a)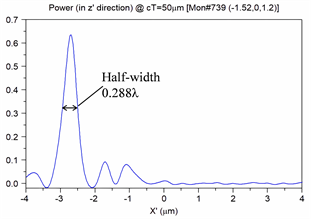
 (b) (c)
(b) (c)
Figure 9. (a) Diagram of the trajectory of the transverse movement of the silicon lens; (b) Relationship between the lateral position of the silicon lens, X, and the imaging properties of the focal point; (c) Full width of the half peak of the image point at X = 0.95
图9. (a) 硅透镜横向移动轨迹图;(b) 硅透镜横向位置X与焦点成像性能的关系;(c) X = 0.95时像点的半峰全宽
3.45。通过横向和纵向调整光子晶体中折射率的分布,成功改善了聚焦效果,将焦点的半峰全宽值减小到了0.341 λ。随后,通过硅透镜曲率优化和位置调整,实现了焦点位置和半峰宽度的进一步优化,得到最小半宽值为0.288 λ。与单一方向梯度折射率渐变模型并使用油浸技术后达到的最佳结果0.34 λ相比,本文提出的双向梯度负折射率模型在焦点处的FWHM值有了显著改善。此外,通过移动硅透镜空间位置,建立了基于MEMS (Micro Electro Mechanical System)技术的动态调焦系统,具有0.13 λ~0.76 λ的亚波长下成像调谐范围,为光学设备性能的提升提供了新途径。虽然在降低半宽上取得了一定成效,但仍需进一步优化能量转化效率和远场高分辨率成像。本研究为相关领域的进一步探索提供了有益参考,为微型化、集成化光学设备的发展奠定了坚实基础。
基金项目
国家自然科学基金(61975122)。
NOTES
*通讯作者。