基于大数据和动力学模型的车轮磨耗预测研究

Research on Wheel Wear Prediction Based on Big Data and Dynamic Model

摘要: 为了研究车轮磨耗的特点和演变过程，对机车车轮的磨耗进行了大数据分析研究发现：轮径及轮缘厚度的磨耗率随轮径值及轮缘厚度的降低呈先减小后增大的趋势、且新轮状态下车轮踏面的磨耗率约为轮缘磨耗率的三倍左右；新轮状态下车轮踏面磨耗较为明显，一定运行里程后轮缘磨耗更为突出。建立了机车动力学模型、轮轨滚动接触模型、材料磨损模型一体的车轮磨耗计算模型，并使用实测车轮数据与优化算法相结合的方式来对车轮磨耗计算模型中磨耗系数k进行优化，计算发现：磨耗系数取平均值的车轮磨耗计算结果与实测值误差较大，而取优化值的计算结果与实测值的误差较小在3%~13%之间(车轮磨耗集中在−45~40 mm，磨耗最大位置在−10~−5 mm之间)。

Abstract: In order to study the characteristics and evolution process of wheel wear, the big data analysis of locomotive wheel wear was carried out, and it was found that: The abrasion rate of wheel diameter and rim thickness decreases first and then increases with the decrease of wheel diameter and rim thickness, and the wear rate of wheel tread is about three times that of the rim wear rate under the new wheel state; The wear of the wheel tread is more obvious in the new wheel state, and the wear of the wheel rim is more prominent after a certain mileage of operation. A wheel wear calculation model integrating the locomotive dynamics model, wheel-rail rolling contact model and material wear model was established. The wear coefficient k in the wheel wear calculation model is optimized by combining the measured wheel data and the optimization algorithm. The results show that the error between the calculated results of wheel wear and the measured value with the average value of the wear coefficient is larger, while the error between the calculated result and the measured value with the optimized value is smaller between 3%~13% (the wheel wear is concentrated in −45~40 mm, and the maximum wear position is between −10~−5 mm).

1. 引言

车轮磨耗是由轮轨间的滚动接触、相对滑动、蠕滑等综合因素引起的；其直观表现为车轮的廓形发生变化，从而影响轮轨间的接触状态，及运行过程中的各项动力学参数及其平稳性和安全性 [1] 。因此快速准确地对车轮磨耗进行预测对延长车轮使用寿命、保证行车安全具有十分重要的意义。

在对车轮磨耗进行计算时，最重要的就是材料磨损模型的选取，常用的材料磨损模型分为两类，一类是基于能量耗散的磨耗功模型，以Zobory模型为主；另一类是基于蠕滑理论的Archard模型，而这两种计算模型都有自身的局限性。邹强 [2] 使用磨耗功模型对车轮踏面损伤进行了预测，但未考虑轮轨间的蠕滑作用所以预测结果误差较大。于春广 [3] 使用磨耗功来定性地评价车轮的磨耗性能，且考虑了三种蠕滑力的影响，但未对接触区域进行黏着和滑动的区分，因此也不能完全准确地对车轮磨耗进行预测。李霞，黄宇峰 [4] [5] 在采用Archard模型对车轮磨耗时为减小误差并节约计算时间，将磨耗系数k直接取为平均值进行计算，虽然预测结果较好，但其预测方法并不利用长运行里程下的磨耗预测。周迅 [6] 基于有限元ALE方法并将磨耗系数取为最小值1 × 10⁻⁵，计算了车轮的磨耗量，发现预测结果与实际磨耗数据略微偏小。赵新光 [7] 将磨耗系数k采用反推法进行较为合理的选取，用Archard模型对机车车轮进行磨耗预测。综上所述目前车轮磨耗预测进行仿真计算时主要存在两个问题：1) 采用磨耗功模型计算时未考虑轮滚间的蠕滑力的影响，且无法对接触区域进行合理的黏着、滑动区分，因此无法准确地实现车轮磨耗。2) 采用Archard模型计算时由于磨耗系数k的非线性等特点无法对其进行统一准确有效的选取，因此即使是采用同样的磨耗预测方法，其结果也会有较大差异。

为解决上述问题，本文在对车轮磨耗进行预测之前先对实测车轮磨耗数据进行分析，得到不同运行里程后车轮廓形的实测数据，并初步研究车轮磨耗的规律；使用Archard模型对车轮磨耗预测进行仿真计算时，使用实测车轮数据与优化算法融合驱动的方式对磨耗系数进行优化选取，并使用FASTSIM算法对接触区域内进行黏着区和滑动区的划分，充分考虑蠕滑力对车轮磨耗的影响，提高车轮磨耗预测模型的可信度。

2. 车轮磨耗大数据分析

本文对实测的车轮磨耗数据进行大数据分析有以下两个目的：

1) 获得一批精确的磨耗后的车轮廓形数据及磨耗量数据，为后文中车轮磨耗预测仿真计算提供实际的对比数据。

2) 初步分析车轮磨耗的部分规律，用以验证后文中磨耗计算模型的准确性及磨耗系数选取的是否合理。

车轮磨耗主要分为轮缘磨耗和踏面磨耗，因此对一大批某HXD型机车的车轮数据进行采集，并做统计分析，主要研究其轮径值和轮缘厚度的变化规律。下面拟合出轮径磨耗率 $V_D$ 、轮缘磨耗率 $V_d$ 随轮径值、轮缘厚度的变化曲线。其中进行以下定义 [8] ：

$\{\begin{array}{l}{V}_D=\frac{D_{t_{m+1}}-D_{t_m}}{t_{m+1}-t_m}\times 5\\ V_d=\frac{d_{t_{m+1}}-d_{t_m}}{t_{m+1}-t_m}\times 5\end{array}$ (1)

上式中的分子分别为每相邻两次实际检测时轮径值和轮缘厚度，分母为两次检测的时间间隔。上式中 $V_D$ 、 $V_d$ 实际意义为每五天，轮径和轮缘厚度的磨耗量。对车轮轮径值及轮缘厚度的众多采样值进行整理筛选，去除脏点，将其最终拟合为误差较小的二次曲线，如下图1、图2所示：

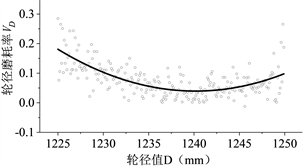
Figure 1. Wheel diameter wear rate fitting curve

图1. 轮径磨耗率拟合曲线

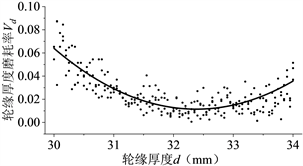
Figure 2. Flange thickness abrasion rate fitting curve

图2. 轮缘厚度磨耗率拟合曲线

轮径和轮缘厚度的磨耗速率拟合曲线为：

$V_D=0.00062D^2-1.523D+984.62$ (2)

$V_d=0.00926d^2-0.5994d+9.717$ (3)

由上图可知：

1) 轮径和轮缘厚度磨耗率随轮径值及轮缘厚度的减小呈先减小后增大的趋势，在轮径值为1240 mm、轮缘厚度为32.37 mm时其磨耗率最小，分别为0.0394、0.0118左右；在新轮状态下轮径的磨耗率约为0.096、轮缘的磨耗率约为0.0307，由此可见轮缘的磨耗率及磨耗量在新轮状态下约为轮径的三分之一左右。

2) 而在运行一段时间后，轮径及轮缘厚度降低，其动力学性能也有所下降，轮轨间的接触更加剧烈，轮径磨耗率几乎是最小值的2~3倍、轮缘磨耗率是最小值的5~6倍，因此需进行镟修，恢复部分轮缘厚度，以降低轮缘和轮径磨耗率，延长使用寿命。

3. 实测车轮数据与优化算法驱动的车轮磨耗预测

3.1. 机车动力学模型

本文选择运用广泛，结构较为简单的HXD1型机车 [9] ，将其简化为1个车体、2个构架、4个轮对、一系悬挂和二系悬挂装置，总共50个自由度，在SIMPACK软件中建立了轴重为25 t的(单节)多刚体机车动力学模型并假定机车的各构件均为刚性体且不发生弹塑性变形，如图3所示。下表1为机车建模的部分主要参数。

在实地调研后将仿真的轨道线路拟定为一条长为2000 m的“S”形双曲线，其中曲线的半径暂定为800 m，线路中曲线的占比约为40% (包括圆曲线和缓和曲线)。若机车通过曲线时的设计时速为100 km/h，则其外轨超高定为150 mm，轨道激励采用现场实测线路时速160 km等级的(哈大线)轨道谱。

机车动力学模型建立后需对轮轨滚动接触问题进行求解，由于本文中轮轨间存在两点接触(轮缘与钢轨、轮缘与踏面)，所以采用非Hertz理论来求解轮轨接触法向问题；采用Kalker简化理论及FASTSIM算法来解决轮轨接触切向问题。

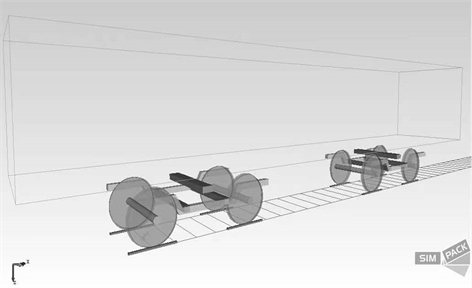
Figure 3. HXD1 locomotive dynamics model

图3. HXD1机车动力学模型

Table 1. Basic parameters for modeling the HXD1 locomotive

表1. 机车建模的基本参数

3.2. 磨耗系数的优化选取

本文采用Archard模型对车轮磨耗进行仿真计算，因此需对磨耗系数k进行合理的选取。JENDEL通过试验提出磨耗系数的取值与接触物体间相对滑动速度和接触压力有关，并分为四个不同的区域 [10] ，如下图4所示：

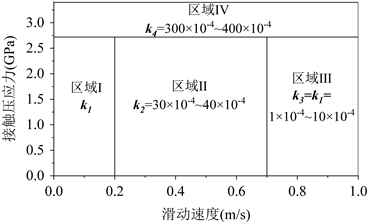
Figure 4. Distribution of wear coefficients in the Archard model

图4. Archard模型中磨耗系数分布

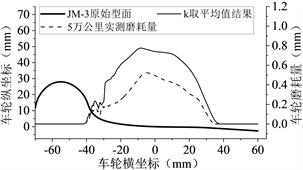
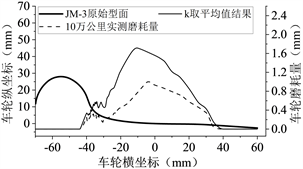
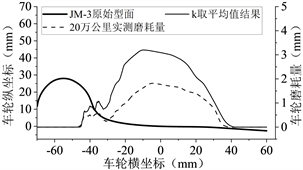
本文开始计算时暂将磨耗系数k分别取平均值，车轮初始型面选择JM3 [11] 型面，车轮的硬度取为3.4 × 10⁹ Pa，对机车运行5万公里、10万公里、15万公里、20万公里采用Archard模型进行磨耗计算，并与实测的车轮廓形进行对比分析。车轮踏面每仿真运行5000公里更新一次，且每次踏面的更新都采用三次样条插值对其进行平滑处理，k取平均值时车轮磨耗的计算结果如下图5所示。

分析发现：当磨耗系数k取平均值进行计算时，0~20万公里内车轮磨耗的分布情况与实测车轮磨耗数据较为相似，都在−45~45 mm之间，这说明仿真计算中轮轨接触模型与实际线路的轮轨接触关系较为吻合；但仿真计算的整体磨耗量要实测数据大很多，这说明磨耗系数k的取值整体偏大，并不能很好地模拟出此运行条件下车轮的磨耗情况，因此需对磨耗系数k进行优化选取，降低仿真计算值与实测值之间的误差。

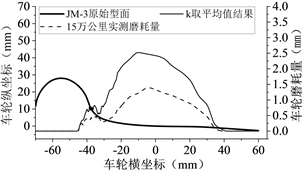
(a) 5万公里对比 (b) 10万公里对比(c) 15万公里对比 (d) 20万公里对比

Figure 5. The abrasion coefficient k was averaged and compared with the wheel wear under different simulated mileages

图5. k取平均值不同仿真里程下车轮磨耗对比

磨耗系数k寻优过程(以运行10万公里为例)：

1) 将实测的多组车轮磨耗数据进行大数据分析，整合出运行10万公里后车轮型面数据，并记每个实测型面数据为 $x_i$ 。

2) 将磨耗系数k取平均值用Archard模型计算10万公里车轮磨耗，其每个型面数据记为 $y_i\left(k\right)$ 。

3) 将每个实测型面数据 $x_i$ 与上述预测型面数据 $y_i\left(k\right)$ 作差，计算其差值的平方和，并记为 $P^2$ ：

$P^2={\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left[x_i-y_i\left(k\right)\right]}^2}\left(i=1,2,3,\cdots ,m\right)$ (4)

4) 以上式中 $P^2$ 为目标函数，通过遗传算法及最小二乘法对其进行多次迭代计算，使其达到最小值时(即所以预测型面数据点 $x_i$ 与实测型面数据点 $y_i\left(k\right)$ 之间的误差最小，型面上数据点的位置最为接近)得到3个磨耗系数k的优化取值：k₁ = 3.23 × 10⁻⁴、k₂ = 33.4 × 10⁻⁴、k₃ = 6.94 × 10⁻⁴。

3.3. 车轮磨耗取优化值计算结果对比

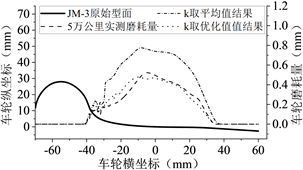
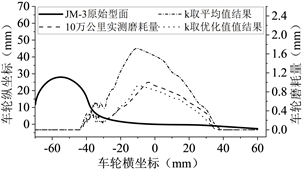
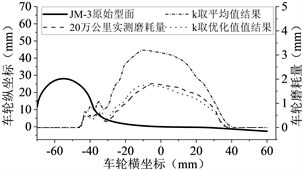
将磨耗系数k取优化值进行仿真计算，其计算的初始条件与上文中完全相同，现将k取优化值预测结果、k取平均值预测结果列出进行对比，将如下图6所示。

为衡量磨耗预测模型的准确度，现将磨耗系数k取平均值和优化值的各项计算误差进行列表对比(包括：百分比相对误差RE、均方根误差RMSE)，如下表2所示。

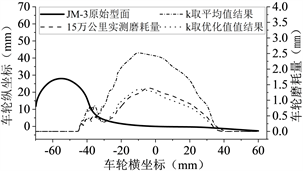
(a) 5万公里对比 (b) 10万公里对比(c) 15万公里对比 (d) 20万公里对比

Figure 6. Comparison of wheel wear under different simulated mileage

图6. 不同仿真里程下车轮磨耗对比

Table 2. The error analysis of the calculation results of different wear coefficients was taken

表2. 取不同磨耗系数计算结果误差分析

分析发现：

1) 将磨耗系数k取平均值的计算结果与实测结果几乎是1.5至1.8倍的关系误差较大；而取优化值的计算结果与实测值误差较小(两种误差都在3%~13%以内)，两者的磨耗分布也很相似(均方根误差RMSE的值较小)。这说明上述车轮磨耗计算模型及磨耗系数的优化选取较为符合实际情况，磨耗系数k的优化选取较为合理，可以以此为基础进行深入研究。

2) 将磨耗系数k取优化值计算时的车轮最大磨耗深度比实测值略小，且其位置更靠近轮缘一侧。这可能是因为设计的线路中曲线占比较实际线路略大大；车轮的硬度选定较大；选择的磨耗系数略微偏小等原因。

3) 车轮磨耗主要发生在踏面及轮缘根部，其范围在−45~40 mm之间，最大磨耗位置主要集中在−10~−5 mm处；踏面磨耗的深度约为轮缘磨耗或轮缘根部磨耗的3倍，这与上述关于车轮磨耗大数据的分析结果较为吻合。

方鑫 [12] 引入遗传算法，对岭回归算法的参数进行调优并开发出“GA-岭回归”预测算法，成功准确的预测了机车车轮磨耗，且其误差控制在0.01~0.09 mm以内。朱爱华 [13] 采用多种优化算法对磨耗系数进行优化，最后发现采用粒子群算法的方法所得出的磨耗系数计算精度最高，其磨耗系数取为k = 2.371。肖国放 [14] 通过摩擦功与Archard模型相结合的方式，发现磨耗系数基本位于I区(轻微磨耗区)，磨耗系数取为k = 3.27较为合理。经与同行业当前的研究结果对比，本文中创新性的使用实测车轮磨耗数据与遗传算法相结合的方法对磨耗系数进行优化选取是可行的；使用优化后的磨耗系数计算出的车轮磨耗的误差也是在可接受范围内；且磨耗系数的取值也较为接近目前同行业中最新的研究结果。

4. 结论

本文通过对车轮磨耗实测数据进行大数据分析和建立机车动力学模型仿真计算相结合的方式对车轮磨耗中最主要的轮缘磨耗和踏面磨耗进行了研究分析，得出以下结论：

1) 经大数据分析发现：轮径、轮缘厚度磨耗速率受轮径值及轮缘厚度的影响很大，当轮径值及轮缘厚度在1240 mm、32.37 mm左右时最小，分别为0.0394、0.0118左右；在新轮状态下，轮缘的磨耗速率约为轮径的三分之一，即在新轮状态下车轮主要发生踏面磨耗。

2) 建立机车动力学模型后采用Archard模型对车轮磨耗进行仿真计算，发现磨耗系数取平均值的预测结果与实测车轮磨耗有较大误差，又创新性地采用实测车轮磨耗数据与遗传算法结合的方式得到3个优化后的磨耗系数k (k₁ = 3.23 × 10⁻⁴、k₂ = 33.4 × 10⁻⁴、k₃ = 6.94 × 10⁻⁴)。

3) 将磨耗系数分取优化值计算发现：取优化值的预测结果与实测车轮磨耗的各项误差保持在3%~12.5%以内，且磨耗分布也较为相似，因此取优化值的方法可以较为准确地对车轮磨耗预测进行仿真计算。车轮磨耗主要发生在踏面及轮缘根部，其范围在−45~40 mm之间，最大磨耗位置主要集中在−10~−5 mm处；随着运行里程的增大，轮缘磨耗的程度加深。

基金项目

国家自然科学基金资助项目(52271023)；辽宁省教育厅科学研究项目(LJKZ0493)；大连市科技创新基金应用基础研究项目(2022JJ12GX029)。