1. 引言
近年来,随着电机应用的多样化,高功率密度、高可靠性和高紧凑性的要求越来越受到重视,温升是限制这三个要求的瓶颈之一,如果温升非常高,将导致电机过热、绝缘失效和退磁等问题。目前电机的冷却方式大概有四种:(1) 空气冷却 [1] ;(2) 水冷 [2] ;(3) 直接油冷 [3] ;(4) 油水联合冷却 [4] ,最佳的冷却性能通常为油冷和水冷的结合,然后是直接油冷、间接水冷和风冷。虽然直接油冷的存在需要更多的成本且导致系统相对复杂,但相反直接油冷却具有以下几个优点:油在为电机提供冷却的同时可为汽车中的旋转部件进行润滑,例如轴承变速箱等 [5] ;油是一种良好的电绝缘体,可以与电有源部件直接接触。
随着永磁同步电机制造技术的发展,需要更准确、更详细的温升计算和冷却分析,才能更好的指导电机的设计和生产。目前最常用的热分析方法主要有公式法、等效热网络法、有限元法、有限体积法。公式法主要是基于经验公式,在准确性方面存在问题,应用相当有限。等效热网络法通过经验公式计算各种电阻,根据几何位置关系和传热路径将各节点进行连接,形成全局热阻网络,从而预测电机内主要部件的温度 [6] 。有限元分析在热分析中模拟固体之间的热传导,采用对流换热边界条件,可以预测整个电机的温度,且准确性相对于等效热网络法而言较高 [7] 。有限体积法主要优势在于它可以解决复杂区域的流动特性,缺点是求解过程较长且对计算机硬件要求很高。
本文以一台额定功率为80 KW的车用油冷式永磁同步电机作为研究对象,结合有限元法和公式法分析计算电机各部件的损耗,并对电机气隙域及绕组部分进行了等效处理,通过计算出电机各表面与冷却油的换热系数,结合有限元方法仿真模拟分析了10,000 rpm额定工况下电机内流动特性和温度分布,为电机设计提供理论依据。
2. 模型建立
2.1. 电机基本参数
本文研究的电机是80 KW油冷式永磁同步电机,该电机的基本参数如表1所示。
2.2. 流动传热模型
SPH方法即光滑粒子流体动力学方法,是新兴的无网格拉格朗日算法,所有质点的整体运动被看作是流体的运动,计算原理是基于插值原理,通过利用核估算式将一个偏微分方程转化为积分形式,这个积分方程在数值上通过一系列离散的质点的总和来逼近 [8] 。SPH方程的构造分为两步,第一步是核函数近似,第二步是“粒子近似”。
(1)
(2)
方程(1)为核函数近似,即将某一点的属性用另一个区域的属性来描述,核函数建立这两者之间的关联;方程(2)为粒子近似,用一系列粒子将这个场离散化;
是主粒子属性;
是相邻粒子属性;粒子属性包括粒子速度、质量、密度和体积等;
是核函数;方程(2)等号右边是相邻粒子的影响求和的离散化形式(下标j代表相邻粒子编号)。
电机内大部分热量都是通过热传导和热对流进行扩散,当使用油冷对电机进行冷却时,通过辐射的散热微不足道,可以忽略不计。热传导是电机内部传热主要方式,然而也有少量热量通过传导传递到环境,相比之下,对流是将热量传递到环境的主要方式。热传导遵循傅里叶定律,热对流满足牛顿冷却定律,其计算公式分别为:
(3)
式中,
为传热面通过的热量;
为材料的导热系数;
为导热面积;
为物体沿n方向的温度变化率;
为热对流传递的热量;
为表面换热系数;
为固体表面温度;
为流体表面温度。
2.3. 损耗模型
电机的热性能主要取决于各种损耗和冷却能力,损耗由不同的机制产生,发生在不同的部件中,在进行热分析之前,准确预测损耗及其分布至关重要 [9] 。
首先,铁损计算主要基于铁损分离理论,最早由Bertotti等人提出,该理论是基于电机各部分在变化磁场作用下铁损机理的差异。分离计算各部分的损耗,最后通过叠加得到电机的总损耗,铁芯损耗分离理论的损耗计算公式如下 [10] :
(4)
式中,
为铁芯总损耗;
为磁滞损耗系数;
为涡流损耗系数;
为附加损耗系数;
为磁场的交变频率;
为磁通密度幅值,表示是磁场的强弱。
计算绕组铜耗,根据焦耳定律,绕组铜损耗等于绕组电流的平方和电阻的乘积。对于三相绕组,每相绕组电流和电阻相同,绕组铜损耗的计算公式为:
(5)
式中,
为电机绕组的电流;
为绕组的电阻。
永磁体涡流损耗可由下式进行计算 [11] :
(6)
式中,
为体积为
的永磁体涡流损耗;
为永磁体涡流密度;
为永磁体的电导率。
3. 温度场求解参数设置
3.1. 假设和等效处理
3.1.1. 基本假设
为了简化电机的三维模型,缩短求解时间,根据电机结构和传热的特点,做出以下假设:
a. 考虑到电机内的热传导和热对流远大于辐射传热,可以忽略电机内部的辐射传热;
b. 由于电机的对称性,在计算过程中使用沿轴向1/2模型;
c. 电机内部材料的导热系数不随温度变化,是恒定的;
d. 电机产生的损耗没有损失,全部用于电机发热。
3.1.2. 等效处理
在热分析中,定子绕组始终是需要关注的部件,是因为绕组是主要热源,并且绝缘材料对高温敏感,其复杂的内部结构使得构建真实模型具有挑战性,因此需要进行等效操作。在这里将绕组等效为具有统一导热系数的均匀铜导体,将绝缘物质等效为厚度均匀的绝缘层,根据下述公式对等效绝缘层导热系数进行计算 [12] :
(7)
式中,
为等效绝缘层导热系数;
为不同绝缘材料的等效对应厚度;
为不同绝缘材料的导热系数。
电机气隙中的空气由于转子的旋转而产生流动,使得定转子和气隙间的换热变得复杂,因此导入气隙等效导热系数,对其进行简化计算,气隙中的空气为湍流状态时,气隙等效导热系数用公式表达为 [13] :
(8)
式中,
为气隙的等效导热系数;
为气隙雷诺数;
为转子外径与定子内径之比。
3.1.3. 材料属性
电机中各部件的材料参数如表2所示。
采用的冷却油物性参数见表3。
3.2. 电机内热源设置
电机的热源通过体热源方式添加,将不同损耗添加到相应的部件模型上,各部件的生热率等于其对应损耗除以体积。由Maxwell结合公式计算得到电机各部件损耗,通过UG测量各部件体积,得到生热率如表4所示。

Table 2. Material parameters of motor components
表2. 电机各部件材料参数

Table 4. Heat generation rate of main parts of motor
表4. 电机主要部件生热率
3.3. 电机各部件换热系数计算
对流换热系数是评价冷却系统对流传热能力的重要指标,直接影响电机的温度,其准确计算至关重要。本研究中对于电机各表面对流换热系数通过经验公式和SPH方法结合进行计算。
从热分析角度来看,机壳将电机内部部件的热量传递到周围环境。电机机壳的外表面,没有强制风冷,通过自然对流进行散热,采用公式(11)计算其表面换热系数 [14] :
(9)
式中,
为电机壳体外部的风速,本研究中假设为0 m/s;
为壳体外环境温度。
经定子油道内流出的冷却油通常对转子的影响并不大,转子部分主要通过其自身的旋转带动与端部空气间的散热,其对流换热系数通过下面公式进行计算 [15] :
(10)
式中,
为转子端面对流换热系数;
为转子端面上的线速度。
定子铁芯是电机磁路的重要组成部分,同时也是主要热源之一,在电机运行时会产生大量损耗,对于电机绕组端部部分,由于其损耗较大且散热不足,因此温度通常高于槽内绕组。本研究中定子铁芯及绕组的冷却方式为直接油冷冷却,定子铁芯通过与定子油道内直接接触的冷却油对流传热,带走热量。冷却油流经定子油道至定子端面后,随后流过端部绕组进行冷却。本研究中,冷却油入口油温为65℃,入口流量为8 L/min,全局液体粒子设为0.5 mm;采用SPH方法计算得到电机定子及绕组表面换热系数如图1所示。

Figure 1. Surface heat transfer coefficient of stator and winding
图1. 定子和绕组表面换热系数
4. 仿真结果及分析
4.1. 冷却油流动特性分析
随电机的运行,定子及绕组表面冷却油液覆盖率逐渐趋于稳定,如图2所示。
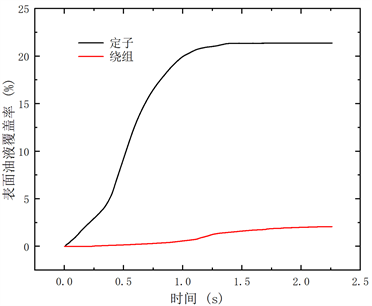
Figure 2. Oil coverage on stator and winding surface
图2. 定子和绕组表面油液覆盖率
当电机油道内稳定流动时,图3为电机内冷却油的速度分布云图,可以看出冷却油在定子油道入口处以及冷却油流出定子油道后至出油口流动速度较快,而在轴向中段圆周油道底部处冷却油流动速度缓慢,存在流动死区,其产生原因可能是受电机油道变化流动路径的影响,当到达某位置后几乎停止流动。图4为电机内冷却油压力分布云图,油道入油口处压力最大为40.6 kPa;出口处与定子油道内流速相比较大,压强最小为0 kPa。在圆周油道与轴向油道连接处,因油道形状产生变化,导致压力变化较大。图5为不同视图下冷却油温度分布云图,从图中可以看出电机内冷却油最低温度为65℃,处于入口处,且沿圆周油道流动时,与发热体定子表面接触位置油温偏高,与机壳表面接触位置油温偏低,随后冷却油在轴向油道内流动时,与定子部件充分接触换热导致冷却油温度明显上升,在与端部绕组位置接触处冷却油达到最高温度。
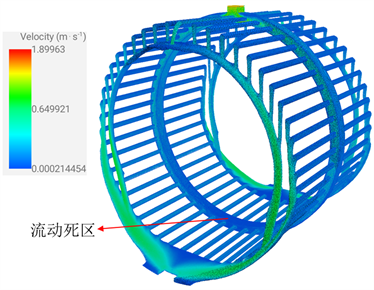
Figure 3.Cooling oil velocity distribution
图3. 冷却油速度分布

Figure 4.Cooling oil pressure distribution
图4. 冷却油压力分布
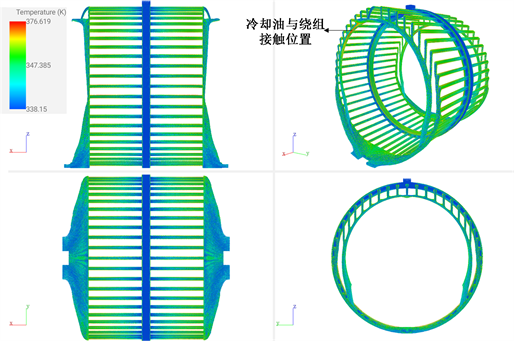
Figure 5. Temperature distribution of cooling oil
图5. 冷却油温度分布
4.2. 电机温度场仿真结果分析
在分析损耗和换热系数后,通过温度场仿真计算可以得到电机内各部件的温度分布。电机绕组及定子铁芯部分温度分布如图6和图7所示,电机内最高温度为145.49℃,出现在绕组处,定子内油道内与端面处与冷却油直接接触换热,带走热量。同时槽内绕组与定子通过热传导传热,导致槽内绕组温度相对于端部绕组温度较低,端部绕组上端通过与定子油道内流出的冷却油直接接触,散热效果较好,最高温度出现在端部绕组下端,该部位无冷却油直接接触,散热较差,同时定子最高温度出现在定子齿与端部绕组接触处,为144.14℃。对于转子部分温度分布,如图8所示,其旋转带动端部空气流动,增强与端部空气的对流散热,导致转子端面处温度较低,由于转子中段散热条件较差,导致越靠近轴向中部位置温度相对越高。
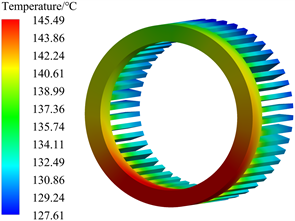
Figure 6. Winding temperature distribution
图6. 绕组温度分布
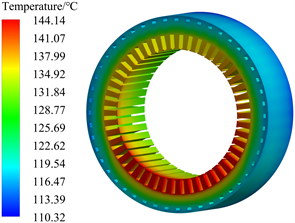
Figure 7. Stator temperature distribution
图7. 定子温度分布
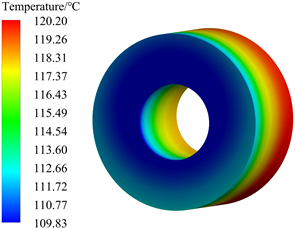
Figure 8. Rotor temperature distribution
图8. 转子温度分布
5. 结论
本文以一台车用油冷式永磁同步电机为例,分析计算了电机在10,000 rpm额定工况下各部件的损耗,采用SPH方法结合经验公式计算电机各表面的对流换热系数,同时结合有限元法对电机流场和温度场进行仿真分析,得到以下结论:
(1) 在仿真时可以将绕组等效为铜导体加绝缘层的方式,提高模型尺寸简化和等效导热系数的确定是提高模型求解速度的关键。
(2) 从流场分析可知,油道内存在冷却油流速极低的流动死区,冷却油压力最大为40.6 kPa,随着冷却油的流动,与发热体定子及绕组接触,冷却油温度呈增大趋势。
(3) 从温度场分析可知,该电机绕组部分温度最高,为145.49℃,采用油冷方式可有效控制电机整体温度,防止电机过热损坏,该仿真为永磁同步电机设计提供了依据,节省电机研发周期。