1. 引言
在现实世界中,确定性是相对的,不确定性是绝对的。现实世界的不确定性主要表现为随机性和模糊性,随机性常用概率表示,模糊性的表示方法有模糊集合论、直觉模糊集合论等,但概率论和模糊集合论都无法同时表现随机性和模糊性。李德毅院士从随机性与模糊性的关联性出发,提出了描述自然语言中概念不确定性的云模型,实现了自然语言表示的定性概念与定量表示的不确定转换,它用于不确定性知识表示非常有效[1] -[4] 。
云模型的确定度类似于模糊集合中的隶属度,反映了模糊性,同时这个值自身也是个随机值,可以用概率分布函数描述,因此,云模型将模糊性和随机性有机地结合起来。但云模型的确定度仅是一个单一的值,在实际应用中,它不能同时表示确定、否定和犹豫的知识,例如在选举投票事件中,除了支持与反对外,经常还有弃权情况发生,因此仅仅用确定度表示模糊性存在一定的问题,本文将直觉模糊集合论的思想与云模型结合,提出了直觉云模型,直觉云模型在定义知识的模糊性时,同时考虑了确定度、否定度和犹豫度三个方面的信息,体现了随机性和直觉模糊性的有机结合;在直觉云模型的基础上结合直觉模糊推理给出了直觉云推理方法,并将其应用于空中目标攻击意图分析中,验证了有效性。
本文第2节给出了基于直觉云模型的不确定性知识表示;第3节详细地介绍了直觉云推理方法;第4节将直觉云推理应用于空中目标攻击意图分析,验证了直觉云推理方法的有效性;第5节对全文进行总结。
2. 直觉云模型
2.1. 直觉云模型定义
定义1设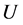 是一个用精确数值表示的定量论域,
是一个用精确数值表示的定量论域,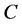 是
是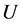 上的定性概念。若定量值
上的定性概念。若定量值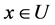 ,是定性概念
,是定性概念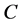 的一个随机实现,
的一个随机实现, 对
对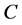 的隶属度
的隶属度 和非隶属度
和非隶属度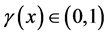 都是具有稳定倾向的随机数
都是具有稳定倾向的随机数
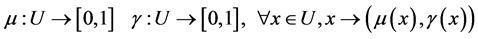
且满足条件
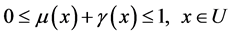
则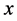 在论域
在论域 上的分布称为直觉云,每个
上的分布称为直觉云,每个 称为直觉云滴,表示为
称为直觉云滴,表示为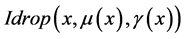 此外
此外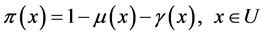 是直觉指数,表示
是直觉指数,表示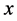 对
对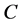 的犹豫度。
的犹豫度。
直觉云分别由确定度云滴和否定度云滴组成,它们是一个定性概念在数量上的一次实现,云滴越多愈能反映定性概念的整体特性。直觉云的确定度类似于直觉模糊集的隶属度,否定度类似于直觉模糊集的非隶属度,反映了定性概念的模糊性,此外,它们本身还是一个随机数,因此,直觉云模型既能表示定量数值与定性概念之间的隶属度和非隶属度,同时又反映了它们的随机性,实现直觉模糊性和随机性的有机结合。
直觉云可以用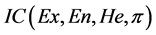 表示,其中,
表示,其中,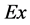 是相应云滴在论域空间上分布的期望,表示定性概念最典型的样本;
是相应云滴在论域空间上分布的期望,表示定性概念最典型的样本; 是直觉指数,表示对定性概念犹豫度的度量;熵
是直觉指数,表示对定性概念犹豫度的度量;熵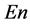 是定性概念的不确定性度量;超熵
是定性概念的不确定性度量;超熵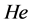 是熵不确定性度量。选择不同的概率分布函数,可以实现不同的直觉云模型。由于正态分布具有普适性,所以通常选择正态直觉云模型。图1是一个一维正态直觉云的示意图,其中直觉指数为0.1。
是熵不确定性度量。选择不同的概率分布函数,可以实现不同的直觉云模型。由于正态分布具有普适性,所以通常选择正态直觉云模型。图1是一个一维正态直觉云的示意图,其中直觉指数为0.1。
2.2. 直觉云发生器
与云模型类似,直觉云模型中定性概念与定量数值之间的转换可以通过直觉云发生器完成的。直觉云发生器主要包括正向直觉云发生器、逆向直觉云发生器、X条件直觉云发生器和Y条件直觉云发生器,本文主要介绍X条件直觉云发生器和逆向直觉云发生器。
1) X条件直觉云发生器
在给定论域空间上,如果已知直觉云的数字特征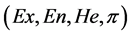 和特定的
和特定的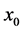 ,那么正向直觉云发生器称为X条件直觉云发生器,如图2所示。X条件直觉云发生器的实现算法如下:
,那么正向直觉云发生器称为X条件直觉云发生器,如图2所示。X条件直觉云发生器的实现算法如下:
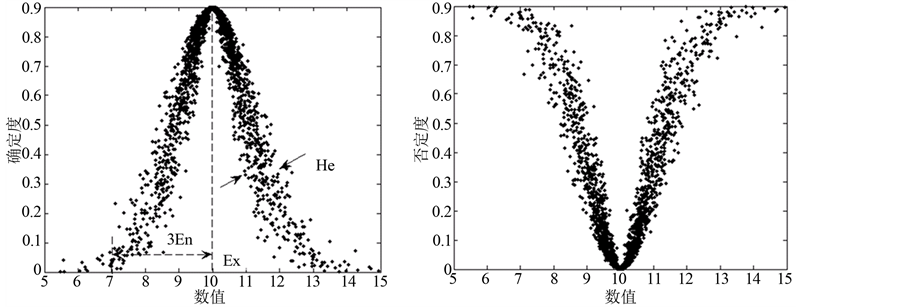 (a) 确定度云 (b)否定度云
(a) 确定度云 (b)否定度云
Figure 1. One dimensional normal intuition cloud diagram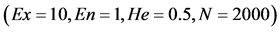
图1. 一维正态直觉云示意图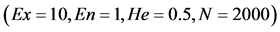

Figure 2. X condition intuition cloud generator
图2. X条件直觉云发生器
输入:定性概念的数字特征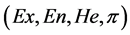 ,特定值
,特定值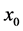
输出:特定值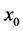 属于定性概念的确定度
属于定性概念的确定度 、不确定度
、不确定度
算法步骤:
1) 生成以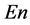 为期望值、
为期望值、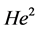 为差的正态随机数
为差的正态随机数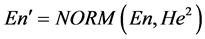 ;
;
2) 计算确定度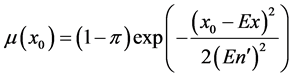 ;
;
3) 计算不确定度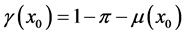 ;
;
2) 逆向直觉云发生器
逆向直觉云发生器是实现数值和相应定性概念之间的不确定性转换模型,是从定量到定性的映射,逆向直觉云发生器如图3所示。
逆向直觉云发生器的实现算法如下:
输入: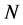 个云滴
个云滴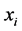 及其确定度
及其确定度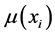 、不确定度
、不确定度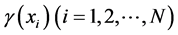
输出:定性概念的数字特征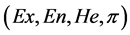
算法步骤:
1) 计算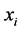 的平均值
的平均值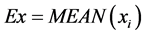 ,得到定性概念的期望;
,得到定性概念的期望;
2) 计算 的方差
的方差 ,得到定性概念的熵;
,得到定性概念的熵;
3) 根据每一个云滴计算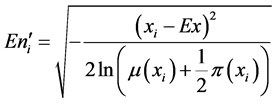 ;
;
4) 计算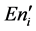 的方差
的方差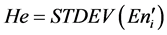 ,得到定性概念的超熵;
,得到定性概念的超熵;
5) 计算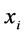 的直觉指数的平均值
的直觉指数的平均值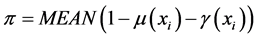 ,得到定性概念的直觉指数。
,得到定性概念的直觉指数。
其中,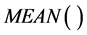 和
和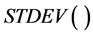 分别为求样本均值和方差的函数。
分别为求样本均值和方差的函数。
3. 直觉云推理方法
文献[5] [6] 给出了云推理的基本思路,本文将他们推广到直觉云模型,给出直觉云推理方法的基本思路。首先,构建前件直觉云发生器,对目标属性进行直觉云转换,实现输入的直觉云模型表示;其次,根据专家知识构建推理规则库,设计直觉云推理算法,并选择合适的解模糊算法;最后,将多次重复推理得到的云滴输入逆向直觉云发生器,得到最终的推理结果。直觉云推理的基本流程如图4所示。
3.1. 推理规则
推理规则采用if A then B的形式,其中A是规则的前件,表示推理的前提条件,B是规则的后件,表示推理的结果。如果前提条件包含多个要素,规则的前件可使用“and”或“or”连接符进行组合,本文采用“and”连接符,例如:
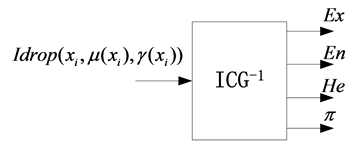
Figure 3. Y condition intuition cloud generator
图3. 逆向直觉云发生器

Figure 4. The basic flow chart of intuition cloud reasoning
图4. 直觉云推理基本流程图

其中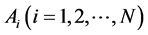 为前提部分定性概念,
为前提部分定性概念,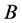 是输出对应的定性概念。推理规则来源于专家知识,同时又要反映一定的客观规律,应具有完备性和合理性。
是输出对应的定性概念。推理规则来源于专家知识,同时又要反映一定的客观规律,应具有完备性和合理性。
3.2. 推理算法
推理算法主要完成已知事实与推理规则的合成,从而获得推理结论。本文借鉴直觉模糊逻辑推理思想,合成算法采用“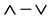 ”。根据直觉模糊逻辑推理法则,每一条推理规则对应一个输入输出关系:
”。根据直觉模糊逻辑推理法则,每一条推理规则对应一个输入输出关系:
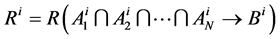
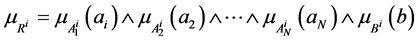
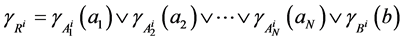
若某一时刻的输入为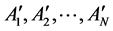 ,由推理规则
,由推理规则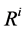 ,得到输出为
,得到输出为
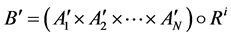
满足
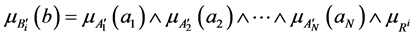

多条规则的合成公式为:
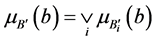
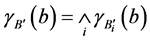
直觉模糊集常用的解模糊算法有最大真值法、重心法、加权平均法等。重心法是将直觉模糊集的隶属度函数和非隶属度函数的真值函数曲线与横坐标围成面积的重心作为推理结果的最终输出。重心法能够比较平滑的输出推理结果,对输入信号的微小变化不敏感,因此本文采用重心法实现推理结果的清晰化,即
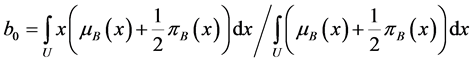
式中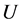 为输出论域,
为输出论域,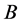 为定义在输出论域上的直觉模糊集。
为定义在输出论域上的直觉模糊集。
3.3. 逆向直觉云发生器
为了消除输入随机性对推理结果的影响,共进行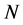 次直觉云推理,获得
次直觉云推理,获得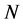 个推理结果云滴,并输入图3所示的逆向云发生器得到最终的推理结果。由统计学原理可知,直觉云滴数越多,逆向直觉云算法的误差越小。文献实验证明,当云滴数大于10时,就能够得到比较准确的期望值。
个推理结果云滴,并输入图3所示的逆向云发生器得到最终的推理结果。由统计学原理可知,直觉云滴数越多,逆向直觉云算法的误差越小。文献实验证明,当云滴数大于10时,就能够得到比较准确的期望值。
4. 基于直觉云推理的空中目标攻击意图分析
空中目标意图攻击分析是现代防空作战中理解战场态势、预测目标行动及威胁的关键,但该问题又是一个研究难点,主要原因是问题求解过程中存在许多不确定性因素。一方面,战场环境下获得的战场信息,由于传感器性能及敌方干扰、欺骗等行为,使得信息存在高度的不确定性;另一方面,由于作战的复杂性,用于推理的军事知识也存在着不确定性,这种不确定性不仅表现为随机性,还表现出一定的模糊性,现有的目标意图分析方法有直觉模糊推理方法[7] [8] ,动态贝叶斯网络方法[9] [10] 、多属性决策方法[11] 、自适应模糊神经推理方法[12] 等,它们都无法同时表示目标信息的随机性和模糊性。为了更好地处理目标意图分析中的不确定性,本文采用直觉云模型表示问题的不确定性,利用直觉云推理实现空中目标攻击意图分析。
4.1. 空中目标攻击意图分析的直觉云模型
当目标的距离相近时,影响空中目标攻击意图分析的因素主要包括目标类型、目标空袭样式(根据目标高度确定)和目标航向角等。根据上述分析,构建了空中目标攻击意图分析属性直觉云模型如图5所示。
4.2. 属性信息的云模型转换
从一级融合中获得的信息既有定量描述的,也有定性描述的,且各信息的取值范围也不同。为了便
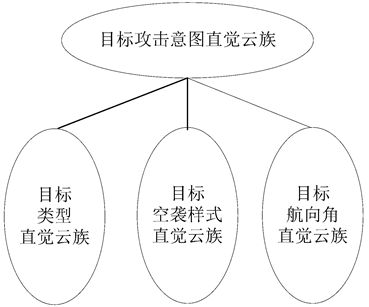
Figure 5. Attribute intuition cloud model of Aerial Target Intention Analysis
图5. 空中目标攻击意图分析属性直觉云模型
于推理,首先将态势信息进行归一化处理,然后再进行直觉云模型转换。其中,态势信息归一化采用文献[11] 中的方法。这里仅给出态势信息的直觉云转换方法。若每一类直觉云对应的定性概念可分为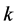 个级别,则在
个级别,则在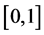 区间定义
区间定义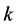 个论域,分别对应相应的级别,熵、超熵和直觉指数根据经验设定。由于正态直觉云具有普适性,所以本文选择正态直觉云,第一级设计为半降正态直觉云,最后一级设计为半升直觉云,其它各级设计为标准正态直觉云。
个论域,分别对应相应的级别,熵、超熵和直觉指数根据经验设定。由于正态直觉云具有普适性,所以本文选择正态直觉云,第一级设计为半降正态直觉云,最后一级设计为半升直觉云,其它各级设计为标准正态直觉云。
目标类型论域为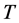 ,其范围为
,其范围为 ,根据目标航向不同可构建3个直觉云:小型目标
,根据目标航向不同可构建3个直觉云:小型目标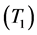 、大型目标
、大型目标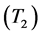 、其他目标
、其他目标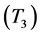 ,相应的直觉云数字特征分别为:
,相应的直觉云数字特征分别为: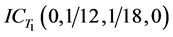 、
、 、
、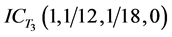 。目标航向角直觉云如图6所示。这里令直觉指数
。目标航向角直觉云如图6所示。这里令直觉指数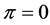 ,这样简化是合理的,因为当
,这样简化是合理的,因为当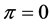 时,非隶属度函数的反制作用或形成的反对程度最强。在这种情况下得出的结论如果是可信的,那么当直觉指数不为0时,所得的结果的可信度将会更高[11] 。
时,非隶属度函数的反制作用或形成的反对程度最强。在这种情况下得出的结论如果是可信的,那么当直觉指数不为0时,所得的结果的可信度将会更高[11] 。
目标航向论域为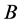 ,其范围为
,其范围为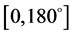 ,根据目标航向不同可构建7个直觉云:径向临近
,根据目标航向不同可构建7个直觉云:径向临近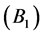 、临近
、临近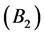 、侧翼临近
、侧翼临近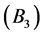 、迂回临近
、迂回临近 、侧迂临近
、侧迂临近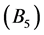 、侧翼
、侧翼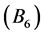 、背离
、背离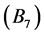 ,相应的直觉云数字特征分别为:
,相应的直觉云数字特征分别为: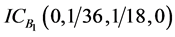 、
、 、
、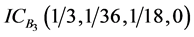 、
、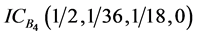 、
、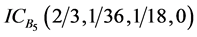 、
、 、
、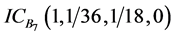 。目标航向角直觉云如图7所示。
。目标航向角直觉云如图7所示。

Figure 6. Intuitive cloud certainty degreeof Target type
图6. 目标类型直觉云确定度示意图
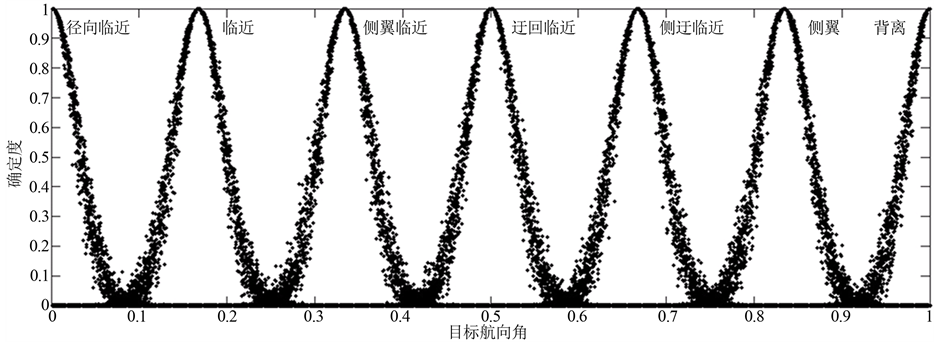
Figure 7. Intuitive cloud certainty degreeof Target heading
图7. 目标航向角直觉云确定度示意图
目标高度论域为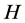 ,其范围为
,其范围为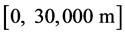 ,构建4个直觉云:超低空
,构建4个直觉云:超低空 、低空
、低空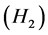 、中空
、中空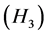 、高空
、高空 ,相应的直觉云数字特征分别为:
,相应的直觉云数字特征分别为: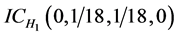 、
、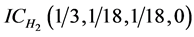 、
、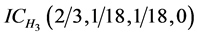 、
、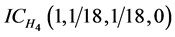 。目标高度直觉云如图8所示。
。目标高度直觉云如图8所示。
目标攻击意图论域构建5个直觉云:极大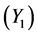 、大
、大 、中等
、中等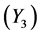 、小
、小 、较小
、较小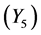 ,相应的直觉云数字特征分别为:
,相应的直觉云数字特征分别为: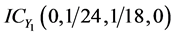 、
、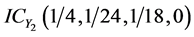 、
、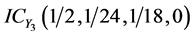 、
、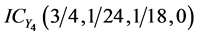 、
、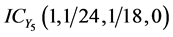 。目标攻击意图直觉云如图9所示。
。目标攻击意图直觉云如图9所示。
4.3. 规则库构建
空中目标意图识别的输入为目标类型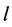 、目标航向角
、目标航向角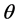 、目标高度
、目标高度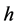 ,每个变量的属性个数分别为
,每个变量的属性个数分别为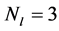 ,
,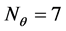 ,
,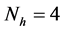 。因此,可以计算出推理规则的总数为
。因此,可以计算出推理规则的总数为 条规则。为了获得高可信度的推理结果,规则越精细越好,但越精细将导致规则增多,出现“组合爆炸”的问题。推理规则的形式为:
条规则。为了获得高可信度的推理结果,规则越精细越好,但越精细将导致规则增多,出现“组合爆炸”的问题。推理规则的形式为:
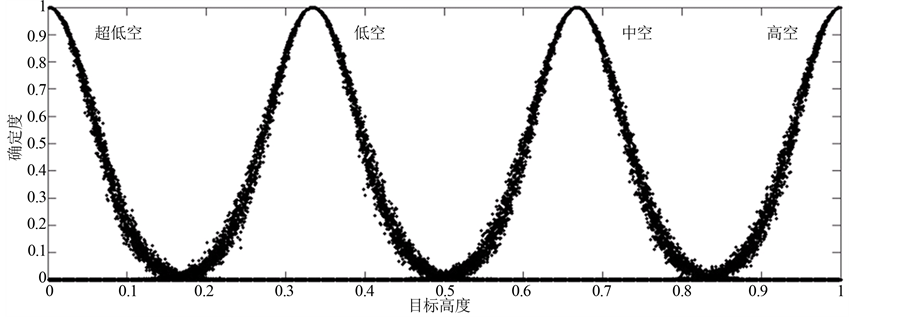
Figure 8.Intuitive cloud certainty degreeof target height
图8. 目标高度直觉云确定度示意图

Figure 9. Intuitive cloud certainty degreeof attacking intention
图9. 目标攻击意图直觉云确定度示意图
4.4. 仿真分析
根据本文提出的算法步骤,在Matlab环境中设计了一个基于直觉云推理的空中目标攻击意图分析系统。表1给出了侦察设备获取的12批敌空中目标信息。
对表1中的目标观测数据进行归一化处理,得到12批敌空中目标属性归一化值,将归一化数据输入推理系统,得到推理结果,如表2所示。
例1 以目标1为例,目标类型为大型目标,高度为6000 m,航向角为0˚,目标属性归一化值为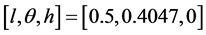 ,由归一化值可知,该大型目标处于低空径向临近状态,其攻击的可能性极大。
,由归一化值可知,该大型目标处于低空径向临近状态,其攻击的可能性极大。

Table 1. The observed value of target
表1. 目标观测值

Table 2. The normalized value of the target attribute and the result of reasoning
表2. 目标属性归一化值及推理结果
将该归一化值输入直觉云推理系统,得到目标攻击可能性为0.9617,攻击意图极大,符合专家经验判断。
例2以目标7为例,目标类型为小型目标,高度为1000 m,航向角为60˚,目标属性归一化值为 ,将该归一化值输入直觉云推理系统,得到目标攻击可能性为0.25,攻击意图小,这是因为小型目标一般指反射面积较小的目标,比如反舰导弹,这些目标在末端雷达开机后,航向角在45˚以内,而目标7的航向角较大,因此其攻击可能性小。
,将该归一化值输入直觉云推理系统,得到目标攻击可能性为0.25,攻击意图小,这是因为小型目标一般指反射面积较小的目标,比如反舰导弹,这些目标在末端雷达开机后,航向角在45˚以内,而目标7的航向角较大,因此其攻击可能性小。
在这12批目标中,目标1、9、10的攻击可能性极大,目标2、5、8、11的攻击可能性大,目标3、4攻击可能性中等,目标6、7攻击可能性小,目标12的攻击可能性极小。
5. 结束语
针对目标属性信息具有不确定性的特点,本文提出了能同时表示直觉模糊性和随机性的直觉云模型,并在此基础上设计了直觉云推理方法,该方法通过构建属性直觉云模型表示信息的不确定性,通过多次重复性的直觉云推理消除数据不确定性对推理结果的影响,推理方法具有很好的容错性和鲁棒性。将该方法应用到空中目标攻击意图分析中,仿真结果表明,本文所提方法简单、有效,为目标意图分析提供了新的思路。