1. 引言
组合结构应用于桥梁工程以来，桥梁承载能力得到了很大提高，同时也大力促进了桥梁工程向大跨、高强方向的发展。其中，波纹钢腹板体外预应力PC组合箱梁桥融合了箱梁、体外预应力和组合结构的优点，正越来越受到国内外工程界的重视，很多专家也对此新型结构进行了探索和研究[1] ，国内学者利用大型有限元软件ANSYS对PBL剪力键进行了分析，分别就剪力键钢板及混凝土应力、模型应变和竖向变形、裂缝及破坏过程分析等三个方面做了较为详细的阐述。
PBL剪力键由带孔的钢板组成，可焊接在工字形截面的上翼缘，孔内可穿入钢筋。浇注混凝土后，孔内的混凝土形成一系列的混凝土棒状榫来抵抗钢构件和混凝土构件之间的竖向掀起，带孔的钢板主要抵抗水平剪力，能在钢与混凝土之间提供强大的连接作用，并具有很好的抗疲劳性能。很多研究表明，PBL剪力键无论在加工制作还是力学性能方面都比传统的剪力连接件有很大的优势[2] 。目前国内外还没有规范对PBL键的形式、尺寸和承载能力作出规定[3] ，而PBL剪力键正是这种结构当中连接钢腹板与上下混凝土翼板的关键部件。因此，对PBL剪力键进行深入细致的分析就显的尤为必要。
2. PBL剪力键承载力理论计算
鉴于剪力键受力情况复杂多变，所以必须在理论分析的基础上，对其进行大量规范化的试验分析。目前很多PBL键试验研究大多借鉴了栓钉连接件的推出试验方法，但试件的形式和尺寸差别较大。国际上对PBL键也没有规定统一的试件和试验标准。
PBL剪力键的极限承载力一般指的是开孔钢板上的单孔极限剪切力。影响其大小的因素很多，如混凝土强度、钢筋的屈服强度、贯穿钢筋直径、钢板开孔直径等等。对于理论计算，下面给出近期一些学者在试验基础得出的计算方法。
Perfobond Strip的剪力键设计公式[4] ：
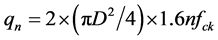(1)
式中：qn为单孔极限承载力(KN/孔)；D为钢板开孔直径(mm)；n为钢板开孔个数；1.6为剪切强度系数；fck为混凝土圆柱体抗压强度(MPa)。此公式要求提供贯穿钢筋，使之围绕孔对孔中混凝土施加约束，使其出于三向受力状态，有利于提高组合结构的整体工作性能。公式表明，单孔的抗剪强度由孔径尺寸和混凝土抗剪强度决定。其破坏模式包括混凝土抗剪销的承压破坏和孔洞间钢板的剪切破坏。
胡建华[5] 等人在PBL剪力键承载力影响因素和计算公式研究中总结得出的剪力键承载力公式：
(2)
式中，Atr为贯通钢筋面积(mm2)；
为普通钢筋面积(mm2)；fy为贯通钢筋屈服强度(MPa)；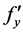
为普通钢筋屈服强度(MPa)；Ac为混凝土榫面积(mm2)；fc为混凝土立方体强度(MPa)；α为钢筋影响系数，取α = 1.320125；β为横向普通钢筋影响系数，当配筋率小于0.18%，取β = 1.042948；γ为混凝土榫影响系数，取γ = 1.95168。
石宵爽，王清远等[6] 在式子(1)基础上提出的改进型计算公式：
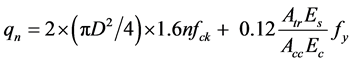(3)
式中：Acc为每个连接件所分配的受剪混凝土面积(mm2)；Atr为贯穿钢筋截面总面积(mm2)；Es为贯穿钢筋弹性模量(MPa)；Ec为混凝土弹性模量(MPa)；fy为贯通钢筋屈服强度(MPa)。此公式考虑工程实用意义，对唯一安全估算承载能力的式(1)做了进一步改进，应用变形协调原理，考虑横向钢筋抵抗滑移的能力，同时考虑了0.12 倍的剪切强度折减系数[6] 。
运用以上公式对本文中的PBL剪力键模型进行承载力计算，模型尺寸为深圳某大桥剪力键实际尺寸[6] ，材料为Q345qc桥梁钢。其中混凝土抗压强度为33.15 MPa，贯穿钢筋为HPB235φ10，剪力件钢材屈服强度为420 MPa。计算结果如表1所示。
公式(3)是鉴于实验结果修正所得的公式，一定程度上能够比较准确地接近实际情况，这样的话，从计算结果可以看出，Perfobond Strip公式计算值偏小，这是因为其所考虑的仅仅只有孔径内混凝土的作用，低估了连接件的承载能力。胡建华等的公式得到的结果也比较准确，能够反映实际情况，这是因为该公式是在大量理论分析与试验基础上总结出来的，与石宵爽，王清远等的修正公式计算结果相差不大。
3. PBL剪力键有限元分析
在有限元分析方面，其有限元分析过程较为繁琐，对于除其试验模型之外的剪力连接件计算没有很强的通用性，目前尚没有利用MIDAS-FEA对PBL剪力键分析的先例。钢和混凝土复合结构有限元分析的最大的难点在于材料模型的准确描述。钢和混凝土复合结构是由钢和混凝土这样两种具有不同物理力学性能的材料组，弹性模量E不是固定不变的，在加载过程中，当混凝土某一部分的应力超出其弹性范围后，弹性模量就会随着应力的变化而变化，材料的σ-ε曲线会变得很复杂。本模型在有限元计算中，钢材取用Q345钢，弹性模量为2.06 × 108g kN/m2，泊松比为0.3；混凝土标号为C50，弹性模量为3.45 × 107 kN/m2，泊松比为0.2。
利用MIDAS FEA建立上文深圳某大桥剪力键有限元模型，混凝土、开孔钢板和工字梁采用实体单元，贯穿钢筋采用钢筋单元，工字梁与开孔钢板用实体布尔并集结合，其与混凝土接触部分建立界面单元。整个模型采用自动划分网格，在实体接触部分，先进行实体分割，其次对相互嵌套接触的实体用布尔差集处理，然后对其接触线面部分进行线播种，最后完成网格耦合操作。
有限元模型及网格划分如图1所示。
对以上模型进行线性静态分析，在工字梁两端施加竖向荷载500KN，可以观察到各个关键点处位移和应力的变化。如图2所示。
在MIDAS FEA中，利用后处理样式的一些操作，可以观察到变形前后剪力键模型的直观变化，另外可以标记出最大最小变形。如图3所示。
随着荷载变化，PBL剪力键各个关键位置最大位移，最大应力变化规律如图4所示。
由图4可见，混凝土和钢板的最大位移呈现类三阶曲线变化趋势，其拐点发生在荷载250 KN左右，
Table 1. Carrying capacity comparison results of PBL shear key
表1. PBL剪力键承载力比较
Figure 1. The finite element model and mesh map of shear key
图1. 剪力键有限元模型及网格划分图
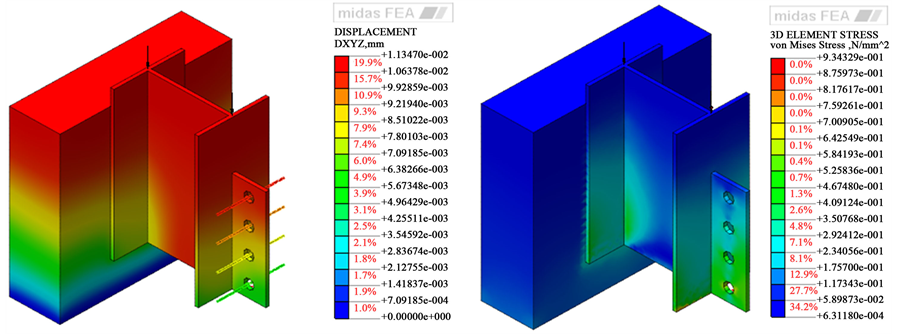
Figure 2. The displacement contours of PBL shear key and FanMises stress cloud
图2. PBL剪力键位移及范梅塞斯应力云图
此时其位移变化率最高。混凝土榫和开孔钢板的最大MISES应力呈相同变化趋势，不同点在于，在100 KN以下时，应力曲线基本重合。这是因为，在较小的荷载作用下，PBL剪力键与混凝土之间基本不存在滑移。因工字梁受集中点荷载作用，在加载过程中，工字梁受力点应力数值较大，一定程度上制约最大荷载的增加，当工字梁受力点应力达到400 MPa时，停止继续加载。
4. 结语
PBL剪力键在桥梁工程中发挥的作用越来越大，对其进行深入研究很有必要。本文从两个方面对其进行了尝试性的讨论分析，一是简要总结了PBL剪力键极限承载力的理论计算，二是利用MIDAS FEA有限元软件对其应力和变形做了简单分析，可以更加直观地认识到其内部应力应变分布变化规律。
运用不同的公式对PBL剪力键承载能力计算结果不同，这主要是因为不同的公式考虑的影响因素不
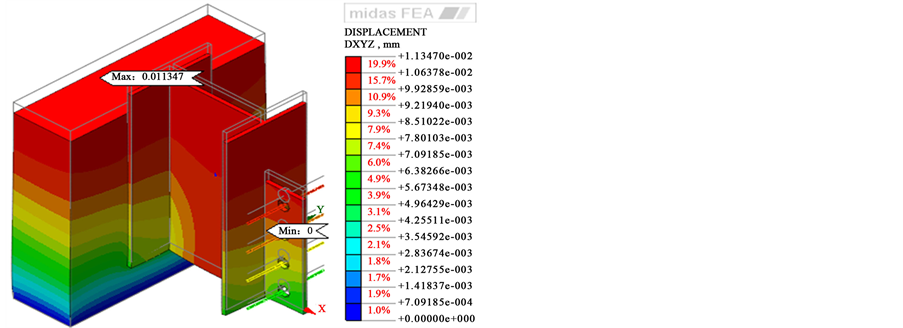
Figure 3. The comparison chart of PBL Shear before and after deformation
图3. PBL剪力键变形前后对比图
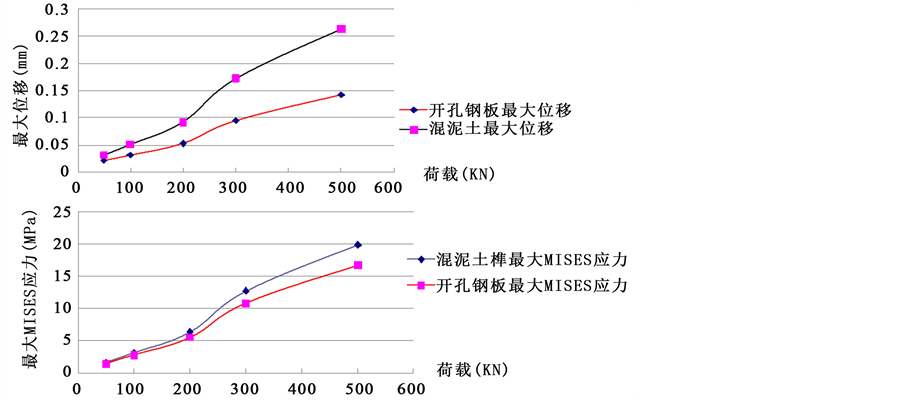
Figure 4. Maximum displacement and stress for some position under different load
图4. 不同荷载下各位置最大位移和最大应力变化规律
同，即使考虑相同因素，由于试验误差的原因，对于公式的修正侧重也有所不同。鉴于没有通用的理论计算公式，这就要求在实际中对于PBL剪力键的分析必须理论与试验相结合，最终得到符合自身实际要求的修正计算公式。利用MIDAS FEA有限元软件对PBL剪力键进行分析，可以直观地了解其内部应力应变变化，跟通用软件ANSYS相比，FEA操作简便，更容易快速得到有限元分析结果。