1. 引言
呼吸系统的气体流动问题在生理学上具有重要的作用,同时也是模拟复杂气体流动和复杂边界条件很好的例子。为了研究由于空气流通所致的吸入毒物或微生物的传播,有必要对呼吸过程进行可视化模拟。本文使用LBM模拟肺的呼吸作用,并把数值模拟结果与生理学现象进行了比较。
近些年,LBM被用于不同的领域进行数值模拟,取得的令人满意的结果[1] -[4] 。如微尺度流动问题[5] ,非牛顿流体流动[6] ,流体固体相互作用问题[7] [8] 等。
肺的呼吸作用是一个动态过程,模拟此过程需要对分形边界和动力学动态过程进行模拟。众所周知,流体流过分形几何体会产生很多特有现象。二维肺部气道是典型的支气管树型分形结构,它服从参考文献[9] 所提出的某些尺度规律。现假设二维肺部气道是对称二叉树。此外,子系分支和母系主支之间的相似率是常数。
过去一些年中,许多生理学家试图从不同方向对呼吸过程进行建模。大多数开展的实验是研究呼吸过程中压力和流量的变化[10] [11] 或是研究分支气道间气体密度,压力,流量之间的关系[12] -[14] 。尽管在呼吸作用建模方向产生了诸多成果,但没有人尝试用格子Boltzmann模型模拟此问题。因此本文从格子Boltzmann模型出发去详细刻画呼吸作用是一项有益的尝试。
本文结构如下:在第二部分,提出了一个基于格子Boltzmann模型模拟呼吸作用换气过程的模型;在第三部分中,我们建立了一个二维肺部模型;第四部分,展示了使用本模型的一个数值例子,并将它们与生理学结果进行了比较。最后,对本文的工作做出了总结。
2. 格子Boltzmann模型
本节引入一个详细模拟呼吸过程的模型。一个完整的格子Boltzmann模型包括离散速度模型(DVM),平衡态分布函数的选取,演化方程三部分。其中最主要的是选取恰当的平衡态分布函数。
对于格子Boltzmann方程:
 (1)
(1)
其中 是在
是在 时刻,位于
时刻,位于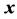 处,具有速度
处,具有速度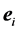 的气体密度平衡态分布函数。其中:
的气体密度平衡态分布函数。其中:
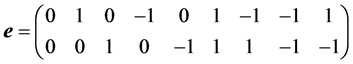

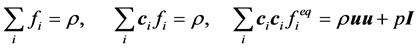
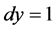 ;
;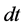 是时间步长,且满足
是时间步长,且满足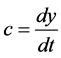 ;
;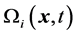 代表碰撞算子,它满足质量和动量守恒;
代表碰撞算子,它满足质量和动量守恒; 是空气密
是空气密
度, 。
。
考虑9格点格子模型,每一个格点都如同图1一样与周围8个格点相邻。如果加上静止粒子,则此种格子模型包含9种粒子移动方向。
对于格子BGK模型,我们选取一个时间松弛逼近:
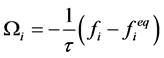 (2)
(2)
其中, 是单松弛时间因子,与流体黏性有关。取
是单松弛时间因子,与流体黏性有关。取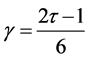 ,得到:
,得到:
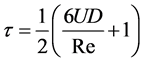 (3)
(3)
在上式中,U 是特征速度;D 是管道的直径即特征长度。对于格子上的各个粒子,选取平衡态分布函数:
 (4)
(4)
式中,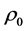 代表空气密度;
代表空气密度;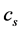 代表声速,
代表声速, 。系数
。系数 通过下式确定:
通过下式确定:
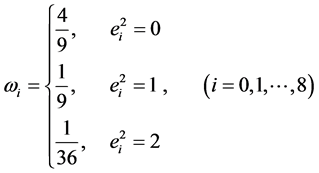 (5)
(5)
考虑边界条件,由文献 [15] 提出的方法,使用与邻近内节点的一阶外插的方法估计非平衡部分。边界节点的分布函数由下式给出:
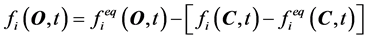 (6)
(6)
上式中C点为与边界节点O邻近的流域内节点。
对于气管顶部和支气管底部的边界条件,由于呼吸作用具有周期性,有必要选择一个周期函数去模拟吸气与呼气,正弦函数是可考虑的周期函数。
入口处边界条件:
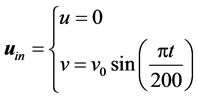 (7)
(7)
出口处边界条件:
1) 如果出口方向平行与 轴,则
轴,则
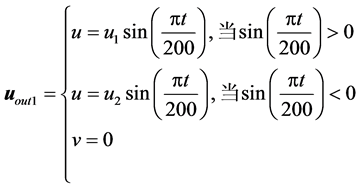 ( 8a )
( 8a )
2) 如果出口方向平行于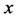 轴,则:
轴,则:
 (8b)
(8b)
3) 如果出口方向平行于直线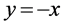 ,则
,则
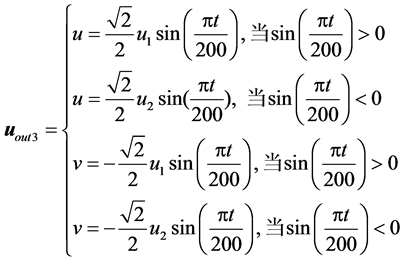 ( 8c )
( 8c )
4) 如果出口方向平行于直线 ,则:
,则:
 (8d)
(8d)
在上述各方程中,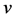 是入口处的空气速度;
是入口处的空气速度; ,
, 是 与支气管树出口处速度有关的系数。在呼吸过程中,吸入空气的速度为
是 与支气管树出口处速度有关的系数。在呼吸过程中,吸入空气的速度为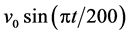 ,同时在支气管末端空气以
,同时在支气管末端空气以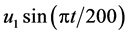 速度流入。呼出气体的流速为
速度流入。呼出气体的流速为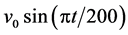 。与此同时,支气管末端气体以
。与此同时,支气管末端气体以 的速度流出。
的速度流出。
考虑本节上述各方程,我们完成了对肺的呼吸作用的建模。
肺部气道具有自相似性,即母系主支与子系分支结构相似。考虑到上述因素,我们提出肺单位的概念。一个肺单位,如图2所示,是由母系主支和子系分支组成。
在图2中,可以明显看到一个肺单位由9个点和4条线段组成。A,B,H,I组成母系主支,B,C,D,E和E,F,G,H是两个子系分支。母子两代具有相同形状,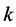 是它们之间的相似率。本文取相似率为定值,
是它们之间的相似率。本文取相似率为定值,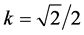 。两个子系分支的分叉角为
。两个子系分支的分叉角为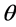 ,
, ,即
,即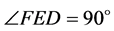 。为估计所有单位和分支,定义m为所研究的分支的代序数,n为所研究分支在同一代的序号。通过代序数m和分支序号n,就可以索引到所要研究的分支。只要已知A,B,I,H点的坐标就可以通过已知的几何知识知道所在的单元内任意点的坐标。通过对每个单元代数及其子分支的坐标迭代,就可以得到一个完整的二维肺部模型,如图3。
。为估计所有单位和分支,定义m为所研究的分支的代序数,n为所研究分支在同一代的序号。通过代序数m和分支序号n,就可以索引到所要研究的分支。只要已知A,B,I,H点的坐标就可以通过已知的几何知识知道所在的单元内任意点的坐标。通过对每个单元代数及其子分支的坐标迭代,就可以得到一个完整的二维肺部模型,如图3。
3. 数值计算和生理学结果的比较
在本部分中,我们的数值结果在图4和图5中展示出来。图4显示的是二维肺模型的压力分布情况,图5显示的是气道内部的流场情况。模拟过程中,选取格子规模为 。各节点的初始速度设为0。粒子的平衡态分布函数被设定为
。各节点的初始速度设为0。粒子的平衡态分布函数被设定为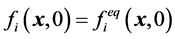 。气管与支气管入口节点密度被固定为
。气管与支气管入口节点密度被固定为

Figure 2. Schematic diagram of a unit of pulmonary
图2. 肺单位示意图
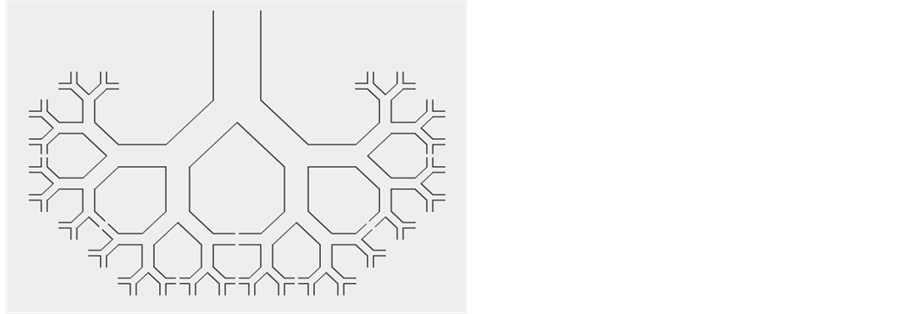
Figure 3. Two-dimensional pulmonary with seven generations
图3. 具有7代肺单元的二维肺模型
 ,与空气密度相当。单松弛时间因子
,与空气密度相当。单松弛时间因子 由式(3)计算所得:
由式(3)计算所得: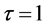 。用非平衡外插方法使得二维肺模型每个边界节点都满足入口或出口边界条件。最后,由于呼吸过程具有周期性,我们需要选定一个时间步作为限制。在这个时间步之后,各节点压力周期性变化。
。用非平衡外插方法使得二维肺模型每个边界节点都满足入口或出口边界条件。最后,由于呼吸过程具有周期性,我们需要选定一个时间步作为限制。在这个时间步之后,各节点压力周期性变化。
数值结果表明,振动的换气气流流过分形结构可以蔓延到周围支气管。除此之外,由气流的速度矢量图,可以看到肺部气道中的空气由于黏性被阻滞在气管与支气管内。
在肺的呼吸过程中,能量耗散单元称为气阻。气阻主要分布于呼吸系统的几个部位:肺部气道内,肺组织中,胸壁腔。本文假定来自肺部气道的气阻起主要作用。肺部气道的气阻主要来自空气在气道内的运动。在数值计算中,我们使用Rohrer公式来量化由于流量变化导致的压力减少:
 (9)
(9)
上式中,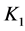 为第一Rohrer系数,单位:kN·sec/m5;
为第一Rohrer系数,单位:kN·sec/m5;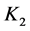 为第二Rohrer系数,单位:kN·sec2/m8;
为第二Rohrer系数,单位:kN·sec2/m8; 表示流体的体积流量,单位m3/sec [16] 。
表示流体的体积流量,单位m3/sec [16] 。
本文中的数值计算工作,初始的速度矢量与实际值成正比。由先前数据,几何上气管的直径取为气管长度的15%。我们取气管直径为1.8 cm,气管长度为12 cm [16] 。因此格子大小为轴向长度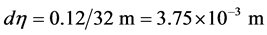 ,径向长度
,径向长度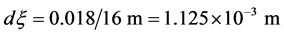 。根据上述数据可以得到
。根据上述数据可以得到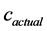 和
和 的比值:
的比值:
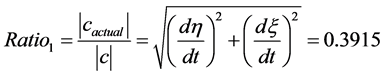
这里, 。
。 与
与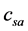 (实际声速)的比值:
(实际声速)的比值:
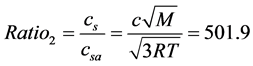
其中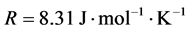 为气体常数。
为气体常数。 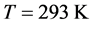 为常温。
为常温。 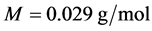 是空气的摩尔质量。
是空气的摩尔质量。 与
与 具有相同的比值:
具有相同的比值:

实际计算中,我们发现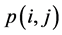 (位置
(位置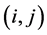 处计算所得的压力)和
处计算所得的压力)和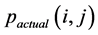 (位置
(位置 实际压力)具有固定比值:
实际压力)具有固定比值:
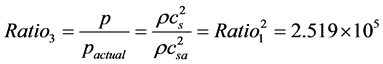
我们找到了使用模型数值计算所得值和实际值的比例。使用这一比例,取系数 ,
,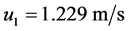 ,
,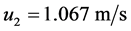 。我们得到
。我们得到 ,
,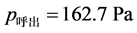 。与标准值
。与标准值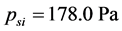 ,
, 进行比较,我们发现数值计算结果满足Rohrer公式。
进行比较,我们发现数值计算结果满足Rohrer公式。
4. 结论
本文提出了一个基于格子Boltzmann模型模拟呼吸作用气体在支气管树内的流动。数值结果表明,振动通气气流流过分形结构可以蔓延到周围支气管,这符合先前的理论结果。我们用此模型模拟了由呼吸造成的气阻并试图让数值结果更加接近Rohrer公式,结果表明当适当调整参数取值,模型可以很好的模拟Rohrer公式。
本文的方法也可以推广到其它分形边界问题中。此模型是二维情形,若要模拟三维情形,则需要添加更多的参数来建立三维支气管树,还需要考虑更多实际因素。
基金项目
本文得到了国家自然科学基金(批准号:11272133)的支助。