1. 引言
犯罪行为是一种地理行为,犯罪行为与地理环境有着密切的关系。随着社会经济的不断发展,犯罪问题尤其是系列犯罪对社会的影响也越来越突出。系列案件由于其作案次数多,作案手段娴熟,反侦察能力强,易造成社会恐慌,所以危害性巨大。但是,系列案件的空间分布格局是有律可循的,依据系列案件发生地点的空间分布格局及相关的内在驱动理论,可以对犯罪人的居住地进行预测,从犯罪地理的角度对系列案件进行侦查。
系列案件的发生具有一定的规律性,作案地点是犯罪人不断选择的结果。解释犯罪与发生地之间关系的理论有日常活动理论、理性选择理论以及犯罪模式理论等环境犯罪学理论。Cohen和Felson提出的日常活动理论指出,犯罪活动与人们的日常活动相关,犯罪人与受害人在时间和空间上必须存在交叉点。当三个元素在时间和空间上出现会聚时,犯罪活动即可能产生。这三个元素分别是:有动机的犯罪人、合适的目标以及有能力的防范力量的缺乏[1] 。理性选择理论由Cornish和Clarke提出,他们认为犯罪行为与其他人类活动一样是选择的结果。这种选择受到费力程度、收获以及付出的成本等权衡过程的影响[2] 。例如,对于入室盗窃案件而言,入室盗窃者会依据出行的成本、入室难易程度、被发现的风险、盗窃收益情况来选择盗窃目标。Brantingham夫妇提出的犯罪模式理论[3] 认为犯罪活动最有可能发生在机会空间(犯罪人感知的包含感兴趣目标的地点)与认知空间(犯罪人拥有具体环境信息的地点,例如他们的住所附近)交叉的地方[4] 。
基于环境犯罪学的相关理论基础,犯罪地理画像是一种利用与系列案件相关联的地点来预测犯罪人可能居住区域的犯罪调查方法,其首要目的是帮助警察部门优选犯罪嫌疑人[5] 。犯罪地理画像最早应用于系列谋杀、强奸、纵火等暴力犯罪的侦查,目前这种侦查技术已在美国、英国、荷兰等欧美国家的警察局得到广泛应用。Rossmo博士的犯罪地理目标模型(CGT)是犯罪地理画像的方法之一,由于具有较好的实战应用效果,已有世界唯一一款成熟的地理画像商业化软件Rigel供部分世界顶级的警察机构使用。但是,在未知犯罪人住处的情况下,需要根据已发生的案件地点推测嫌疑人可能的作案空间习惯,并利用空间点分布情况拟合CGT模型中的参数,因此不同研究区不同犯罪人的最佳距离拟合算法也不相同。
在对空间点分布的研究中,一系列综合距离算法[6] 被提出用以描述空间点群的内部情况,例如质心距离用来描述点群的中心分布趋势,以质心表示点群的中心位置;标准距离又称标准差距离,它衡量了不同点群内部的空间离散程度;不同于质心距离描述了点群的中心分布趋势,平均最邻近距离量化了点群内点间的距离分布情况,表明了点群随机分布的程度,由此得到的平均最邻近指数更加明显的揭示了点群的分布情况,如离散分布、随机分布以及聚集分布。这些算法可以用来拟合CGT模型中的未知参数,提高模型预测的精度,如Rossmo使用平均最邻近距离的一半进行模型拟合取得了最佳的预测效果。
2005年以来,犯罪地理画像理论被逐渐引入国内[7] -[9] ,但是由于国内犯罪数据的敏感性与保密性,目前我国犯罪地理画像研究仅仅限于理论介绍与探讨,缺乏实例研究,更缺乏对于模型中涉及的具体参数的讨论。因此,本文依据CGT模型的理论基础,结合国内两个城市的真实入室盗窃案例数据,研究系列入室盗窃案件的犯罪活动距离特征,并基于CGT模型对不同的点群综合距离算法进行优化选择,探索CGT模型中最佳的参数拟合方法,尝试为警务部门提供高效的地理侦查策略。
2. 方法
2.1. 犯罪地理目标模型
2.1.1. 犯罪地理目标模型(CGT)算法
依据案件点与犯罪人居住点之间的联系以及环境犯罪学的相关理论,将地图划分为大小合适的格网,通过CGT模型算法计算每个网格的犯罪人居住概率值,得到完整的概率表面,并基于概率表面预测犯罪人可能的居住地点。具体概率计算方法是[5] :
对于地图上的任一格网点 ,该点犯罪人居住的概率为:
,该点犯罪人居住的概率为:
 (1)
(1)
式中, 是犯罪人居住在格网点
是犯罪人居住在格网点 的概率值,是每一个犯罪地点计算得到的概率的累加概率。概率计算公式实际上是一个分段函数,用权重系数
的概率值,是每一个犯罪地点计算得到的概率的累加概率。概率计算公式实际上是一个分段函数,用权重系数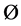 来控制:
来控制:
 (2)
(2)
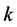 是一个常数,用来放大整体的概率数值;
是一个常数,用来放大整体的概率数值;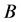 是缓冲区的半径,代表了犯罪人“心理缓冲区”的距离,
是缓冲区的半径,代表了犯罪人“心理缓冲区”的距离, 是犯罪地点的个数;
是犯罪地点的个数; 和
和 均为经验值常数;
均为经验值常数;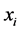 ,
,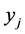 是第
是第 行,第
行,第 列对应格网点的坐标值;
列对应格网点的坐标值;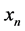 ,
,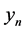 是第
是第 个犯罪地点的坐标值。
个犯罪地点的坐标值。
在模型的计算过程中,需要首先确定参与计算的地图范围,参与计算的地图面积大小也影响了格网大小的划分。CGT模型将参与计算的地图范围确定为略大于包含所有犯罪地点的矩形区域。
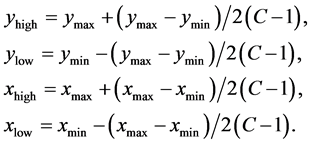 (3)
(3)
式中, 和
和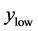 是矩形区域的最大和最小
是矩形区域的最大和最小 坐标,
坐标, 和
和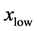 是矩形区域的最大和最小
是矩形区域的最大和最小 坐标;
坐标; 和
和 是所有案件点中的最大和最小
是所有案件点中的最大和最小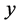 坐标,
坐标,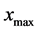 和
和 是所有案件点中的最大和最小
是所有案件点中的最大和最小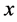 坐标;
坐标;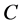 是案件点总数。
是案件点总数。
2.1.2. 犯罪距离衰减曲线
CGT模型中最为重要的参数即为缓冲区B,它代表了犯罪人在多次作案过程中逐渐形成的“心理缓冲区”,即在这个距离上作案达到了犯罪人犯罪风险与收益的平衡。环境犯罪学认为犯罪是犯罪人和他们所处环境相互作用的产物[3] ,系列案件的犯罪人具有一定的认知空间,这种认知空间随着作案次数的增多越来越成熟,犯罪人会从自己的认知空间中选择合适的目标。认知空间源于犯罪人的心理地图,一些有价值的地点如地界标识以及重要建筑等会成为心理地图的锚点,并由此构建犯罪出行的线路、距离或固定的往返路网。Brantingham夫妇认为,犯罪侵害目标的选择实际上是一个动态的过程,即犯罪人在自己熟悉的空间内遇有合适的侵害目标就会发生犯罪,犯罪人会从这些熟悉空间内的地点开始向外围搜寻目标,这种搜寻符合帕累托函数曲线[5] 。Rossmo在研究系列杀人案件时,基于Brantingham夫妇的研究基础,认为在多次作案后,犯罪人会围绕其住所形成一个“心理缓冲区”。在这个区域内,犯罪人往往很少下手,越过这个区域后,随着距离的增加,犯罪人的出行成本以及对作案地区的陌生程度也逐渐增加,作案的概率也逐渐降低。通过对出行距离与案件个数的关系研究,可以得到存在一个峰值的距离衰减曲线,峰值对应的距离范围即可认为是犯罪人“心理缓冲区”的距离范围,也就是CGT模型中缓冲区B的值(图1)。
Rossmo通过模拟犯罪人最佳犯罪活动距离曲线以确定类似案件未知犯罪人最有可能的居住地点。在CGT模型中,经验性常数f和g决定了距离衰减曲线陡峭、平缓程度,缓冲区B则反映了犯罪人犯罪时的出行距离,对模型的预测精度影响很大。每个犯罪人在作案时的“心理缓冲区”都不相同,但是所犯案件点的空间分布一定程度上反映了犯罪人的出行情况,因此可根据案件点群内部的综合距离算法模拟犯罪人最有可能的作案“心理缓冲区”位置。
2.2. 数据
本文选择中国南部沿海G省的Q市、S市两市的城区作为研究区域(图2),其中Q市城区位于G省中部,地势城区较平坦,以第二、第三产业为主;S市地处G省北部,城区地貌以山地、丘陵、盆地为主,地势周高中低,自然矿产资源丰富,第一产业在产业结构中所占比重较高。本文以两个不同地理、人文环境的样区研究系列入室盗窃案件犯罪活动距离的特点,以期获得该类案件犯罪人的活动规律。
本文原始数据来源于G省相关警务部门,选择Q、S两市2001-2013间的9433起入室盗窃案件及已

Figure 1. Decay curve of crime distance [5]
图1. 犯罪距离衰减曲线[5]
破案件的嫌疑人信息。数据包含犯罪人、案件、地图三类数据。犯罪人信息包括犯罪人基本信息、户籍地、现居住地、文化程度等等;案件信息包括案件发生地点、时间、状态、作案工具、作案手段等等。所有数据均为关系型存储,无空间信息;地图数据为基础地理信息数据,包括行政区划、植被、水系、道路网等,以ESRI的shp图层文件存储。
为了发现系列入室盗窃案件犯罪人的犯罪活动规律,本文在原始数据中抽取已破案的犯罪次数为5次及以上的犯罪人所作的入室盗窃案件。原始案件和嫌疑人地址均为地址描述,需要进行地址匹配和空间定位。通过数据筛选和匹配定位,排除地址信息不清无法空间定位的案件数据,本文最终使用的数据为18名犯罪人的237起入室盗窃案件,平均每人作案13起,其中包含Q市城区10名犯罪人(代号:Q_1~Q_10)的123起入室盗窃案件(平均每人12起,最多22起,最少6起,中位数为10起)以及S市城区8名犯罪人(代号:S_1~S_8)的114起入室盗窃案件(平均每人14起,最多27起,最少5起,中位数为13起)(表1)。

Table 1. Statistics of data for processed cases
表1. 处理后案件数据统计表
2.3. 研究方法
2.3.1. 犯罪活动距离曲线
为了得到研究区案件的犯罪活动距离曲线,首先测算每个犯罪人的居住地与其犯罪地点之间的距离,以犯罪人居住地为原点,0.5 km为间隔,统计每个区间内的案件频数。然后以距离为横轴,案件频数为纵轴绘制犯罪距离形态曲线。分别统计两个研究区内的犯罪距离形态,以区别不同自然、社会环境对犯罪活动距离的影响。
在统计犯罪距离形态时,本文选择欧式距离、曼哈顿距离以及最短路径距离三种距离模式进行统计分析。欧式距离是指两点之间的直线距离,不考虑格网型路网的影响;曼哈顿距离是两点间的直角折线距离,适用于路网呈规则格网分布的城市;最短路径距离是利用GIS空间分析中的网络分析,依据道路拓扑计算两点间的最短路径,得到的结果最为接近实际情况(本文考虑犯罪人在犯罪活动中选择最短路径出行)。
2.3.2. 空间点群综合距离算法
CGT模型中k为放大系数,用来调整所有格网点的整体概率值,g和f为经验性的常数(例如Stevenson等拟合出g、f值均为1.2 [10] ),不同案件类型不同研究区该值可能有所不同。为了获得研究样区的经验性常数g和f的数值,本文从两个研究样区的18名犯罪人种随机选择10名犯罪人及其犯罪地点进行参数拟合,每个样区5名犯罪人,并用拟合的参数对剩下的8名犯罪人进行预测(表2)。参数拟合在Matlab软件中实现,查看g和f所有拟合值的分布情况,取频数最大的g和f的值进行模型计算。
在未知犯罪人居住地点的情况下,需要通过用案件点群内的综合距离算法拟合可能的缓冲区B值。在确定g、f参数之后,分别使用平均最邻近距离一半(SNND)、平均最邻近距离(NND)、平均最远距离一半(SFND)、平均最远距离(FND)、点间平均距离(IPD)、标准距离(SD)以及质心距离(CD)距离模拟缓冲区B的值进行CGT模型预测。
点间平均最邻近距离是指所有点与其最邻近的点之间距离的平均值;平均最远距离是指所有点与其最远点之间距离的平均值;点间平均距离是指所有点间距离的平均值;质心距离是每个点与质心点之间距离的平均值;标准距离的表达式为:
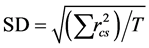 (4)
(4)
其中,SD表示标准距离值, 表示第
表示第 个点与质心的距离,
个点与质心的距离, 是点的总数。标准距离可以测量点在质心周围的集中或分散的程度。
是点的总数。标准距离可以测量点在质心周围的集中或分散的程度。
2.3.3. 犯罪地理目标模型预测精度评价
对除去拟合样本的剩下8名犯罪人的犯罪数据进行模型预测,得到不同预测值的概率表面,其中概率值最高点即为犯罪人最可能的居住地点。本文将预测得到的犯罪人居住地点与实际犯罪人居住地进行比较,测算二者之间的欧式距离,得到预测样本的距离误差。为消除由于案件点分布范围差异造成的距离误差值相差过大,将距离误差与犯罪人所作系列案件中最远两点间距离进行比较,所占百分比越小则

Table 2. Fitting and forecasting samples
表2. 拟合和预测样本说明
侦查时排查范围越小,预测精度越高。
 (5)
(5)
最后为综合比较每种距离算法确定的缓冲区B值对模型预测精度的影响,以误差百分比的均方根误差(RMSE)为综合指标,确定最适合模拟缓冲区B值的距离算法。
 (6)
(6)
其中, 为均方根误差(RMSE),为误差百分比,n为预测样本数。
为均方根误差(RMSE),为误差百分比,n为预测样本数。
3. 结果与分析
3.1. Q、S两市系列入室盗窃案件的犯罪活动距离
图3所示曲线显示了研究区系列入室盗窃案件的犯罪距离形态,其中欧式距离量度的峰值位置以及犯罪最远距离均小于曼哈顿距离和真实路网距离。Q市城区犯罪人犯罪活动欧式距离量度的峰值在1~1.5 km范围内,3 km以外的犯罪次数极少,这与国内研究者对系列入室盗窃案件犯罪活动距离的研究结果一致,赵勇等[11] 对上海市686名系列入室盗窃案件的犯罪人进行调查,得到他们的犯罪活动欧式距离在1~1.5 km范围内。此外,该结果也与北美和英国研究的入室盗窃活动平均欧式距离为1~2英里(1.61~3.22 km)基本一致[12] -[15] ,Sarangi等研究的印度Rourkela和Keonjhar市系列入室盗窃活动平均欧式距离为1.62~1.74 km [16] ;曼哈顿距离量度的峰值在1.5~2 km范围内,3.5 km以外的犯罪次数极少;真实路径距离量度的峰值在1.5~2.5 km范围内,4 km以外的犯罪次数极少。S市城区总体上表现出与Q市城区的一致性,但是每种距离量度的峰值距离小于Q市城区,这可能与S市城区地形起伏大,城市中心区分布紧凑有关。
由于Q、S两市城区的道路网络大体上呈格网型分布,所以从不同距离量度的犯罪活动距离曲线形态上来看,曼哈顿距离量度更接近于真实路网的最短路径距离。本文选择曼哈顿距离进行后续参数拟合以及模型预测,以降低地理画像模型的计算复杂度。
犯罪活动距离曲线同样也验证了系列入室盗窃案件犯罪距离衰减的现象。犯罪人在多次犯罪后会形成自己特定的犯罪活动距离,并在此距离处多次作案。这个距离被认为是犯罪人的心理舒适区,保持了风险与收益最大化的平衡。

Figure 3. Crime distance curve for serial-burglary cases in the research area
图3. 研究样区系列入室盗窃案件犯罪距离曲线
3.2. 点群综合距离算法拟合缓冲区的预测精度比较
通过已有样本数据的拟合,确定CGT模型参数g和f的值分别为0.3和2,这在两个研究样区表现出了一致性。g和f的值决定了距离衰减曲线的陡峭或平缓程度,缓冲区B的值则决定了曲线的峰值位置。由表3、表4可以看出,在众多点群综合距离算法中,Q市城区使用案件点间标准距离(SD)作为缓冲区得到的预测效果最好,平均误差距离为0.523 km,平均误差百分比为15.99%,RMSE值为0.187;S市城区则使用案件点间平均最邻近距离一半(SNND)作为缓冲区得到的预测效果最好,平均误差距离0.384 km,平均误差百分比为6.07%,RMSE值为0.064。
3.3. 点群综合距离算法优化
平均最邻近距离表示了点的空间分布模式,一定程度上反映了点是聚集分布、随机分布还是离散分布。Rossmo的CGT模型在预测系列杀人案件犯罪人的居住地时,使用案件点间平均最邻近距离的一半作为缓冲区进行模型计算,取得了较好的预测效果[17] 。本文的一个研究样区(Q市城区)则得到了与之不同的结论,使用案件点间标准距离作为缓冲区得到了较好的预测效果。表3显示了Q市城区使用标准距

Table 3. Error of predicted distance for city Q (unit: km)
表3. Q市城区预测误差表(单位:km)

Table 4. Error of predicted distance for city S (unit: km)
表4. S市城区预测误差表(单位:km)
离作为缓冲区的预测精度显著高于Rossmo的选择,得到的平均距离误差为0.523 km,平均误差百分比为15.99%,RMSE值为0.187(使用平均最邻近距离的一半进行计算时,此三项值分别为0.965 km,29.03%,0.298)。标准距离是依据标准差来衡量点围绕质心点空间分散程度的量度,由于Q市城区地势相对平坦,系列入室盗窃案件围绕居住地点一定距离范围内分布,因此标准距离更加代表了Q市城区入室盗窃犯罪点的空间分布形态。另一个研究样区(S市城区)则表现出了和Rossmo结论的一致性,这可能跟研究样区地处山区,地形起伏大,案件分布较为聚集有关。(图4~图6)
4. 结论与讨论
本文依据犯罪地理目标模型(CGT)对国内两个研究区的系列入室盗窃案件进行了地理画像,取得了较好的预测效果,将案件的侦查范围缩小至案件整体分布面积的15%以内,并可根据生成的概率表面概率值区间确定侦查地区的优先次序,为系列案件的侦破提供参考。同时,基于不同距离算法的犯罪人“心理缓冲区”模拟,确定了不同研究区最合适的点群综合距离算法,一定程度上提高了地理画像的预测精度。
总体来看,本文两个研究区的系列入室盗窃案件犯罪人的犯罪活动距离相对较短,在1~1.5 km范围内(欧式距离),这与国内其他研究者以及欧美研究者对同类型犯罪活动距离的结果基本一致,比系列杀人等暴力刑事案件的犯罪活动距离近的多。这是因为入室盗窃案件的风险比其他暴力刑事案件低,在综合

Figure 4. Distribution of case points in city Q for offender Q_4 (left) and Q_6 (right)
图4. Q市城区某犯罪人Q_4(左)及Q_6(右)案件点分布图
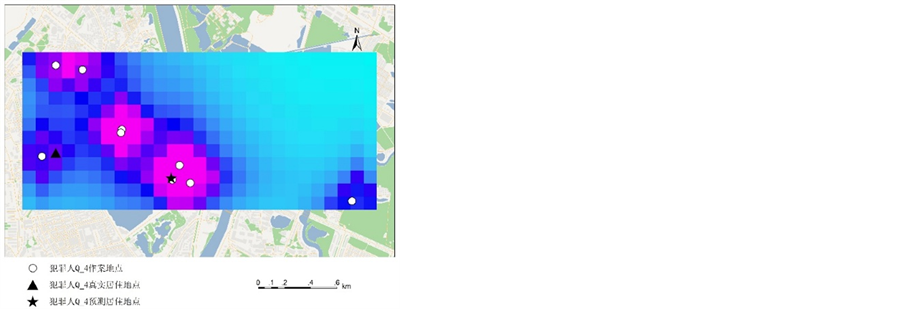
Figure 5. Prediction result for offender Q_4 (left) and Q_6 (right) using the traditional CGT model
图5. 犯罪人Q_4(左)及Q_6(右)传统CGT模型预测结果

Figure 6. Prediction result for offender Q_4 (left) and Q_6 (right) using the standard distance algorithm
图6. 犯罪人Q_4(左)及Q_6(右)使用标准距离算法预测结果
考虑出行成本、犯罪风险与收益时,其平衡点的位置也距离其居住地点相对而言近的多。
在空间点群综合距离算法优化选择上,两个研究区的结果具有差异性。Q市城区用其案件点的标准距离表示每个犯罪人的“心理缓冲区”更为合适,预测的精度也最高,而S市城区则表现出与Rossmo相同的结论,使用案件点间平均最邻近距离的一半进行拟合与预测取得了较好的效果。因此,对于系列入室盗窃案件这种案件类型而言,不同研究区选择固定的点群综合距离算法模拟CGT模型中缓冲区B的值并不科学。文中的数据结果显示出不同研究区需要根据其地理环境、人文因素等综合考虑去选择合适的点分布模式算法,不存在最合适算法的情况。
本文选择的两个研究区地形、社会结构差异明显,研究结果可以为国内地理画像的实例研究提供一定的参考。但是模型仅考虑距离因素,模糊了地形、文化、社会结构等每种因子对犯罪人作案选择的单独影响力,也限制了模型预测的精度。被模糊的地形、社会结构、文化因子对作案地点选择的影响也将在接下来的研究中提取成为各个单一的影响因子,作为地理画像模型的修正,探究犯罪人在选择作案地点时的决策过程。
致谢
感谢华南师范大学研究生科研创新基金项目对本研究的支持,感谢相关警务部门及企事业单位对本文研究的数据支持。
基金项目
华南师范大学研究生科研创新基金资助(项目号:2013kyjj058)。