1. 引言
低频交变电场在金属导线内的速度，可以简称为交流电的速度。这个问题长期以来被电磁学家们忽视。主要原因是，交变电场在金属导线内的速度不是常数，它与电路参数相关。所以人们在没有精确实验数据的情况下，电磁学教课书一般假定电路中低频交变电场的速度就是光速，或者是低于光速 [1] - [4] 。
根据我们近期的实验数据，交变纵向电场在金属导线内的速度不是常数，它与电路参数相关。在大多数情况下，交变电场的速度是低于光速的。可是，在特定的电路参数情况下，交变电场的速度可以超过光速20倍以上 [5] 。
在文献 [5] 中，我们给出了特别设定的电路参数。由函数发生器作为信号源，产生频率为1~10 MHz的正弦交变电场信号。在函数发生器输出端有一个“双通”元件，分别连接一根短的铜导线以及一根长的铜导线。短铜线长度为0.4 m，长铜线长度为6.4 m。二根铜线的另一端分别连接到数值示波器的二个通道。函数发生器与示波器的端口外圈由长度为0.4 m的短铜线连接，作为共地。示波器的输入阻抗选择为1 MΩ。示波器显示的红线代表通过0.4 m导线的交变信号，蓝线代表通过6.4 m导线的交变信号。示波器显示图像的纵座标代表测量到的电压，横座标代表测量到的时间。这样，交变信号通过二根不同长度的导线的时间差就在示波器上明确地显示出来。为了保证测量的可信度，我们把长铜线从6.4 m改为9.4 m，重复进行了测量。实验结果表明，在小于3 MHz的频率区，纵向交变电场的速度超过光速20倍以上。这里作为例子，我们仅仅给出示波器的一个显示图。
在图1中，延迟时间差的显示是0.5 ns，由于本实验中示波器测量时间的精度是±0.5 ns，所以实验结果的延迟时间差可以表示为：0.5 ± 0.5 ns。在本实验中，长度差是6.0 m，工作频率是2.0 MHz。如果定义交变电场的速度是长度差除以延迟时间差，那么从图1我们得到的时间差，交流电场的速度是光速的20倍以上。
2. 实验的原理图
我们日常应用的50 Hz交流电，是典型的超低频的似稳电场，它具有库伦电场的无旋纵场的特性。在低频交流电路理论中，起主导作用的是由电源产生的交变电动势，电路中的电阻和电感。联系这些电路参数的公式是具有感抗的欧姆定律。实验和理论表明，对于频率是10 GHz以下的交变电场，欧姆定律都有效。我们实验中研究的是1~3 MHz的交变电场，所以是属于低频电场。
我们实验的原理图如图2。
在我们的实验中，它是二个不规则形状的RL电路的并联电路。这里
和
分别代表短导线和长导
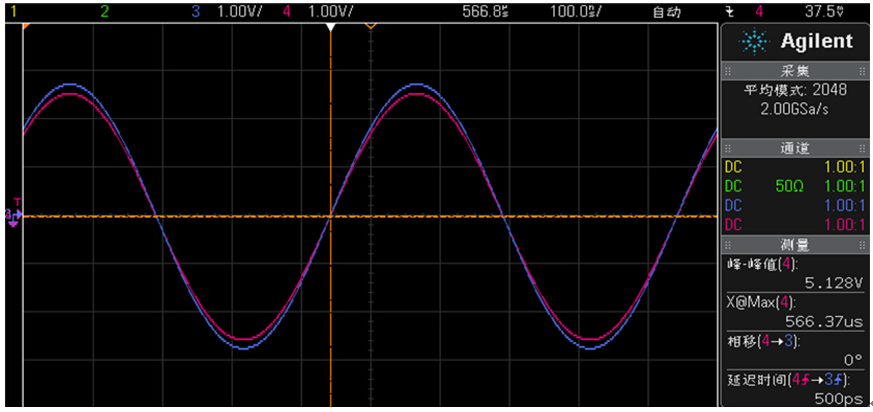
Figure 1.Display of time delay, 6.0 m, 2.0 MHz
图1. 延迟时间差的显示，6.0 m，2.0 MHz
Figure 2. Schematic diagram of RL circuit
图2. RL电路示意图
线的自感。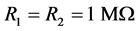
。在实验中，整个电路的尺度不超过4米。短导线的
回路与长导线的
回路事实上是在不同的方向。这样的电路设计是不能用“传输线理论”进行理论计算的。这里，我们直接应用交流电路的欧姆定律，计算RL电路的时间延迟。
带有电感的交流电路的欧姆定律可以写为：
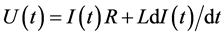(1)
在式(1)中，
代表电动势，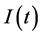
代表电路中的电流，
代表电阻，
代表电感。
式(1)其实隐含了一个基本假定：交变纵向电场是非局域的。也就是说，交变电动势瞬时地把电场传送到电路中导线和电阻的每个部分。
由于金属导线中存在电感，使得电路中的交变电场产生了微小的时间延迟。直导线的电感值由以下近似公式计算：
(2)
在式(2)中，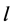
为导线长度，
为导线截面的半径。长度以m为单位取数值，计算结果单位是H (亨利)。通过计算，可得直径为1.0 mm，长度为0.4 m的铜导线的分布电感为530 nH；长度为6.4 m的铜导线的分布电感为11.2 μH。由于0.8 m导线的分布电感为1.0 μH，对于2 MHz信号，它的阻抗大约为12 Ω；6.8 m导线的分布电感为12 μH，对于2 MHz的信号，阻抗大约为150 Ω。而示波器选择的输入阻抗是1 MΩ，所以无论是12 Ω还是150 Ω，相对于1 MΩ的输入阻抗而言，均是很小的。
我们的实验数据表明，在信号频率超过3 MHz以后，通过6.4 m导线的信号会出现一定的幅度改变。而通过0.4 m导线的红线信号要在更高的频率时才会出现此现象。与此同时，示波器显示的相位也出现明显的位移。这二个现象很可能是由导线的电感与示波器内部的电容和电感相互作用导致的。在示波器端口的内部一般有25 pF的电容，这个电容以及端口附近的分布电容对于交变信号的时间延迟是有一些影响的。可是，在我们的实验中，我们关注的是二个交变信号的时间差，所以示波器端口电容的效应被减掉了。
在实验过程中，我们首先交换两个示波器通道，表明交变信号无变化，这说明示波器的二个通道性能一致。
3. 导线中交变电场的速度公式
对于一个RL电路，交变电流可以用指数形式表示
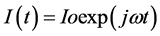(3)
这里，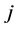
代表虚数。于是带有电感的欧姆定律式(1)可以写为：
(4)
在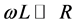
的条件下，式(4)可以改写成为
(5)
在式(5)中，
代表相位角：
(6)
所以，在RL电路中，电阻R上的电压与电动势
相比较存在一个时间延迟：
(7)
令RL电路的回路总长度为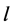
，它近似于导线的总长度。我们把导线中交变电场速度定义为：
(8)
对于单根导线，我们令导线的单位长度的电感
，那么交变电场的速度为
(9)
这里R是RL回路的总电阻。
对于6米长的铜导线，分布电感
大约为1.8 μH。在我们的实验中，电阻
是1 MΩ。根据公式(9)，我们得到
的理论值：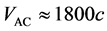
，
代表光速。
从我们的多次测量，对于频率在3.0 MHz以下的信号，纵向电场的速度超过光速20倍以上。这是与公式(9)的理论值相符合的。我们也进行过这样的条件试验：在示波器的二个输入端口分别并联一个1 kΩ的电阻，我们测量到的
。这个实验结果是与公式(9)得到的
理论值相一致的。
4. 讨论
我们需要强调出，本文讨论的金属导体中的纵向电场速度不能与电磁波在金属导体中的传播混为一谈。电磁波是横波，低频电磁波在在金属导体中的传播速度是非常小的，比如400 Hz时只有约10米/秒 [6] 。
然而，电源产生的交变电动势几乎是瞬时地、非定域地作用在电路中导体的各个部分。根据电流在金属导线内的经典微观理论，自由电子在纵向电场的作用下，沿电场强度E方向有定向的飘移，产生了电流，从而使得纵向电场沿导线有个重新分布。也由于金属导线自身分布电感与长度有关，所以纵向电场的时间延迟与频率以及导线长度有关。在我们的实验中，从时间延迟计算得到的交变电场速度代表电场的信号速度，或者是导体内的能流速度。
根据式(5)，电路中的交变电场具有频率以及相位的特征，可是不存在波长的定义。电路中的交变电场信号既不是电磁横波，也不是纵波。交变电场信号是导线中每一部分的电场在进行“纵向同步震荡”，它们的相位随时间同步变化。由于示波器的设计有周期性的扫描功能，它把相位随时间的同步变化在示波器的横向坐标显示出来。这里我可以用下面一个比喻来说明。例如，在舞台上有一排机器人演员，他们在原地跳起动作整齐的“摇摆舞”。每一个机器人演员都是独立的。他们的能量以及舞蹈节奏直接来源于电源的电动势。所以，交变电场的能量以及信号是随时间同步变化的，它不是“行波”。既然电路中的纵向交变电场不是波，于是它不存在波长的定义，也没有群速度的定义。
更加明确地说，在交流电路的情况，电源产生的交变电动势直接把能量和信息以纵场的形式同步地传送给电路的各个部分。这种传送能量的方式与电磁波是完全不同的。
电路中交变电场是非局域的。电源的交变电动势几乎瞬时地把电场传送到电路中导线以及电阻的每个部分。本文定义的交变电场速度，即公式(9)，体现了交变电场的这种非局域性。
关于与本文有关的超光速研究，可参见文献 [7] - [12] 。
致谢
本文作者感谢樊京博士以及艾仓先生，他们重复了本文的实验，并且得到了基本相同的实验结果。作者也感谢褚君浩教授的有益讨论。