1. 引言
近年来,随着我国经济的迅猛发展,人类对能源的需求量在不断的增加,能源消耗量也随之与日俱增,能源消费量与碳排放存在紧密的联系。据有关资料显示,世界能源需求的80%~85%来源于化石燃料,而每年使用化石燃料产生的碳排放量约占大气中碳排放总量的70%,化石燃料燃烧是目前大气中碳增加的首要原因[1] 。大气中碳含量的增加,必然导致人们的健康受损,生态环境也会遭到破坏。为了降低碳排放,从能源本身来讲需要减少能源的消耗量。因此,做好能源消费总量预测研究工作,不仅为相关部门制定科学的能源战略规划和合理的能源消费政策提供依据,也有助于保护生态环境和人类的健康,促进我国经济健康、持续的发展,这具有非常重要的现实意义和战略意义。
一直以来,能耗问题备受大家的关注,国内很多学者对我国能源消费总量问题进行研究分析,他们采用的预测方法各式各样。目前组合预测模型备受欢迎,建立组合预测模型最关键的是确定各单一模型的权重系数。确定权重的方法有很多,如黄宜[2] 等建立指数平滑模型和系统动力学模型分别对云南省能源消费进行预测,然后运用合作博弈中的Shapley值方法确定综合预测模型中各单一模型权重(通过分配总误差),由于Shapley值法具有对合作的各方公平且易接受的特点,故本文采用该方法确定预测模型的权重能够提高预测的可靠性;邓鸿鹄[3] 根据不同权重系数计算方法,构建了基于均方误差非最优权重组合法和最小误差平方和为目标函数最优权重线性组合法的组合模型,分别对北京市能源消费进行预测,结果表明组合模型提高了预测精度且前者组合模型预测效果没有后者好;常建娥和蒋太立[4] 运用层次分析法确定组合预测模型中各单一模型的权重系数,该方法思想简洁,灵活性大,主要用于多目标决策中,特别适用于缺少定量数据进行定性判断的情况;熊浩云[5] 等分别使用神经网络和时间序列法对我国能源消费总量进行预测,然后依据标准差法对各模型所占权重分配,进而建立我国能源消费的组合预测模型,组合预测模型不但克服了单一模型的缺陷,而且提高了预测精度;张志朝[6] 综合各个模型的优缺点,使组合预测误差平方和达到最小,从而确定各单一预测方法的权重系数,得到最优线性组合预测模型,最终对安徽省人均GDP进行预测,研究结果表明该模型预测可靠性较高;江正华[7] 在网络信息资源评价的应用研究中,基于最小方差原理,把运用熵权模糊综合评判法求得的客观权重与运用层次分析法求得的主观权重进行最优化组合,计算出组合权重,从而修正了单一模型所确定的单纯主观或客观权重这样就能够根据专家调查的指标得分,建立基于方差的最优组合赋权网站评价模型,使评判结果更具科学、合理。
基于能源对人类的重要性,做好云南省未来能源消费总量预测工作意义重大,可以为云南省政府制定合理的能源战略及规划提供科学依据,保障云南省能源的合理利用以及健康稳定的发展。本文在一些学者研究的基础上,建立了基于几种单一预测模型的非最优权重线性组合模型,并通过均方误差确定各模型的权重。为了提高预测精度,综合考虑各单一模型的优缺点,采用最小误差平方和法确定这些单一模型的权重系数,最终得到最优权重线性组合预测模型,然后对云南省未来能源消费总量进行预测,其预测效果优于各单一模型和非最优权重线性组合预测模型。
2. 模型及方法
2.1. 组合预测模型的基本介绍
所谓组合预测模型,就是在几种单一预测模型的基础上,采用赋权方式构建模型。由于单一预测模型往往只能够反映能源系统的局部信息,而将其进行有机组合,可以弥补单一模型的不足,提高预测精度,较全面的描述能源系统的趋势。本文就是采用组合预测模型对云南省能源消费总量进行预测分析的,这可使所预测的信息更加全面,预测的结果更加可靠。
然而建立组合预测模型的关键在于各单一模型在组合模型中所占权重的计算,目前计算权重的方法有很多,如层次分析法、Shapley值法、标准差法和最小化方差法等等。根据不同权重系数的计算方法,组合预测模型可划分为两种,即非最优权重线性组合预测模型和最优权重线性组合预测模型。本文则分别采用基于均方误差的非最优权重线性组合法和基于最小预测误差平方和为目标函数的最优权重线性组合法来构建云南省能源消费总量的组合预测模型。
2.2. 非最优权重线性组合预测模型
参考文献[3] ,知非最优权重线性组合模型是通过均方误差来计算各单一模型权重系数的一种组合预测模型,其基本原理是:对均方误差较小的单一预测模型可以赋予较大的权重,而对均方误差较大的单一预测模型则赋予较小的权重。该组合预测模型的构建过程如下:
1) 分别计算各单一预测模型的均方误差 :
:

其中: 为第
为第 个模型在第
个模型在第 期的预测误差;
期的预测误差; 为预测期数;
为预测期数; 为第
为第 个模型的均方误差。
个模型的均方误差。
2) 分别计算各单一预测模型的权重系数 :
:
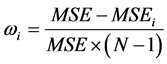
其中: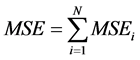 ;
; 表示第
表示第 个模型在组合模型中所占的权重,且各个权重必须满足条件
个模型在组合模型中所占的权重,且各个权重必须满足条件 ,
, 表示单一预测模型的个数。
表示单一预测模型的个数。
3) 非最优权重线性组合预测模型为:

其中: 为组合预测模型的拟合序列;
为组合预测模型的拟合序列;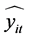 为第
为第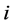 个单一预测模型的拟合序列。
个单一预测模型的拟合序列。
2.3. 最优权重线性组合预测模型
根据文献[3] ,获悉最优权重线性组合预测模型是通过使组合预测误差平方和最小,确定各单一预测模型权重系数得到的组合模型。该模型构建的基本原理是:通过赋予各单一预测模型合适的权重后,使得组合模型得到的预测值与实际值之间的误差平方和达到最小。具体建模过程如下:
令实际的能源消费总量序列为 ;
; 表示组合预测模型的拟合序列;第
表示组合预测模型的拟合序列;第 个单一预测模型的拟合序列记为
个单一预测模型的拟合序列记为 ,
, 表示第
表示第 个模型在组合模型中所占的权重。实际值与组合预测模型拟合值之间的误差序列记为
个模型在组合模型中所占的权重。实际值与组合预测模型拟合值之间的误差序列记为 ,权重系数矩阵
,权重系数矩阵 ,其中
,其中 表示单一预测模型的个数,
表示单一预测模型的个数,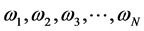 分别表示每个单一预测模型的权重系数。该组合预测模型记作:
分别表示每个单一预测模型的权重系数。该组合预测模型记作:
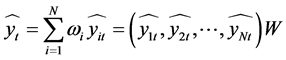
则实际值与模型拟合值的误差序列为:
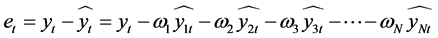 (1)
(1)
对(1)整理得:

建立目标函数:误差平方和
现在最关键的是求解一个 ,使误差平方和
,使误差平方和 达到最小,且权重系数矩阵
达到最小,且权重系数矩阵 需满足:
需满足: ,
, 。
。
上述问题显然是一个最优化问题,因此,使用matlab软件可以求得单一预测模型的权重系数矩阵 ,从而得到最优权重线性组合预测模型
,从而得到最优权重线性组合预测模型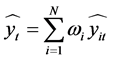 。
。
3. 实证分析
3.1. 数据来源及说明
本文从2011和2012年《云南省统计年鉴》[8] 获取了1978到2011年云南省的能源消费总量数据,我们用1978~2007年的数据建立预测模型,而2008~2011年的数据用于检验所建模型的拟合精度,从而确定预测效果最好的模型。
令云南省1978~2007年实际能源消费总量序列为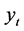 ,其中
,其中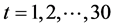 (1978年对应
(1978年对应 ),时间
),时间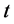 为自变量,
为自变量,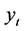 为因变量。
为因变量。
3.2. 建立云南省能源消费总量预测模型
3.2.1. 建立单一预测模型
运用SPSS软件绘制1978年~2007年云南省能源消费总量与时间t的散点图,见图1。
观察散点图,根据云南省能源消费总量的变化趋势,尝试建立二次函数模型、三次曲线模型和指数模型对其预测分析。
对云南省能源消费总量做上述三种回归分析,我们可以得到以时间 为自变量,云南省能源消费总量
为自变量,云南省能源消费总量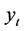 为因变量的预测模型表达式为:
为因变量的预测模型表达式为:
二次函数模型:
 (2)
(2)
三次曲线模型:

Figure 1. Scatter graph of total energy consumption
图1. 能源消费总量的散点图
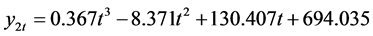 (3)
(3)
指数模型:
 (4)
(4)
其中上述三个式子中,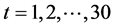 。
。
根据(2)、(3)和(4)式,可以分别求得二次函数模型、三次曲线模型和指数模型对云南省能源消费总量的拟合值 、
、 以及
以及 。
。
根据云南省能源消费总量的真实值与预测值以及公式(5),可以求得各个模型的平均相对误差绝对值,即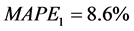 ,
, ,
,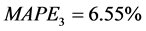 ,且
,且 。
。
 (5)
(5)
3.2.2. 建立组合预测模型
虽然上面几种曲线模型中指数模型的拟合效果相对较好,但无论我们选择哪个模型,最终都会损失部分有用的信息。因此,我们考虑给这些简单的模型赋予合适的权重使其有机结合,构建组合预测模型。这就能够克服单一预测模型的缺陷,提高预测精度,充分利用简单模型提供的全部信息,准确分析现象存在的规律,使得预测效果优于单一模型。下面分别基于二次函数模型、三次曲线模型和指数模型这三个单一预测模型,建立非最优和最优权重线性组合模型对云南省能源消费总量进行预测。
由于本文使用的数据为时间序列数据,而且根据图1,我们发现云南省能源消费总量随时间基本趋于稳定的变化,因此,我们不妨做如下假设:
假设一:云南省能源消费总量随时间变化相对稳定;
假设二:云南省产业结构变化、技术进步等因素不会引起能源消费的显著变化。
1) 建立非最优权重线性组合预测模型
现在对二次函数模型、三次曲线模型以及指数模型赋予合适的权重,建立组合预测模型。根据2.2对非最优权重线性组合预测模型建立方法的介绍,则该组合预测模型的建模过程如下:
a) 根据公式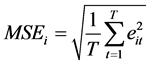 (
( ,
, ),分别计算二次函数模型、三次曲线模型以及指数模型的均方误差为:
),分别计算二次函数模型、三次曲线模型以及指数模型的均方误差为: ,
, ,
,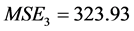 。
。
b) 根据公式 (
( ,
, ,
, ),分别计算二次函数模
),分别计算二次函数模
型、三次曲线模型以及指数模型在组合模型中所占的权重系数为: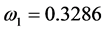 ,
, ,
, ,且各个权重满足条件
,且各个权重满足条件 。
。
c) 由a)和b),得到非最优权重线性组合预测模型为:
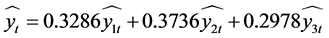 (6)
(6)
其中: 为二次函数模型的拟合序列;
为二次函数模型的拟合序列;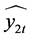 为三次曲线模型的拟合序列;
为三次曲线模型的拟合序列; 为指数模型的拟合序列。
为指数模型的拟合序列。
根据(6)式,可以得到云南省1978~2007年能源消费总量的拟合序列,从而计算出非最优权重线性组合预测模型的平均相对误差绝对值为 。
。
2) 建立最优权重线性组合预测模型
根据2.3对最优权重线性组合预测模型的介绍,我们知道该方法的基本原理是以误差平方和作为目标函数,在一定的约束条件下,求得该目标函数的最小值,从而确定各单一模型的权重系数。该组合预测模型的建模过程如下:
令1978年~2007年云南省能源实际消费总量序列为 ,二次模型的拟合序列为
,二次模型的拟合序列为 ,三次模型的拟合序列为
,三次模型的拟合序列为 ,指数模型的拟合序列为
,指数模型的拟合序列为 ,组合模型的拟合序列为
,组合模型的拟合序列为 ,则实际值与模型拟合值的误差序列为
,则实际值与模型拟合值的误差序列为 ;
; 分别表示二次曲线模型、三次曲线模型和指数模型的权重系数,
分别表示二次曲线模型、三次曲线模型和指数模型的权重系数,
 且
且 ,权重系数矩阵记作
,权重系数矩阵记作 。现需求解以下最优化问题:
。现需求解以下最优化问题:
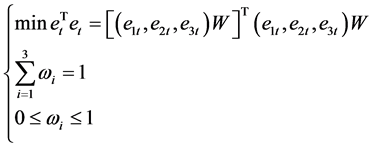
预测云南省能源消费总量的组合预测模型表达式为:

则实际值与模型拟合值的误差序列为:
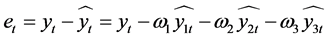 (7)
(7)
对(7)整理得:

使用matlab软件求得单一预测模型的权重系数矩阵
从而得到最优权重线性组合预测模型为:
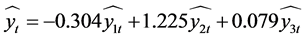 (8)
(8)
通过模型(8),对云南省1978~2007年的能源消费总量进行预测,得到预测值,然后根据输出结果,计算出组合预测模型的平均相对误差绝对值为 。
。
3.2.3. 单一预测模型与组合预测模型拟合精度比较
上文通过建立三种单一预测模型即二次函数模型、三次曲线模型以及指数模型和两种组合预测模型(非最优权重和最优权重线性组合模型)分别对1978年至2007年云南省能源消费总量进行预测分析。各个预测模型的平均相对误差绝对值见表1。
由表1可知,非最优权重线性组合预测模型的拟合误差小于三种单一预测模型;虽然最优权重线性组合预测模型的拟合误差与二次函数模型和三次曲线模型差不多,且明显比指数模型的预测误差大,但是通过各个模型的拟合结果,可以得到它的误差平方和为1299694.846,小于其他三个单一预测模型相应的误差平方和。综上考虑,组合预测模型的拟合精度较高,其预测结果可靠。
现在通过单一预测模型和组合预测模型分别对2008年~2011年云南省能源消费总量进行预测,由此进一步比较简单模型和组合模型的拟合精度。预测结果见表2。
由表2可以发现:非最优和最优权重线性组合预测模型对2008~2011年云南省能源消费总量的拟合误差都比二次函数模型和指数模型的小。根据表2中的相对误差绝对值,可以计算得到二次函数模型、三次曲线模型、指数模型、非最优权重线性组合模型以及最优权重线性组合模型拟合的平均相对误差绝对值分别为8.3%、3.3%、13.7%、5.6%和5.5%。从平均相对误差来看,虽然三次曲线模型的相对小于组合预测模型,但由于单一模型不能够全面反映所研究的问题,因而综合理论与实际考虑,组合预测模型的拟合效果优于简单模型。本文中两种组合预测模型相比较而言,最优权重线性组合模型预测精度高于非最优权重线性组合模型。
4. 组合预测模型对未来云南省能源消费总量预测的应用
综上分析可知组合预测模型的预测效果整体上要优于单一预测模型,现在选用最优权重线性组合模型对云南省未2015年~2019年的能源消费总量进行预测分析。预测结果见表3。
5. 结论
通过上面的实证分析,可以得到以下结论:
1) 从理论与实际意义上考虑,组合预测模型综合了各个简单模型的全部有用信息,克服了单一预测模型的缺陷,提高了预测的准确程度,能够较全面的描述问题;
2) 未来几年内云南省能源消费总量在持续不断的增加,到2020年将达到16982.4万吨标准煤。随着

Table 1. The absolute value of the average relative error
表1. 平均相对误差绝对值

Table 2. The prediction, actual, absolute value of the relative error from 2008 to 2011
表2. 2008~2011年预测值和真实值以及相对误差绝对值

Table 3. Prediction results of energy consumption in Yunnan Province from 2015 to 2019
表3. 2015~2019年云南省能源消费总量预测结果
经济的快速发展,能源需求也在不断的增加,而能源的过度消耗,将导致云南省未来能源供求紧张,生态环境遭到破坏,人们的健康也会受损。从长远来看,如果不适当控制能源的消耗,将会给国家的经济社会发展和人类的健康带来灾难。因此,准确的预测能源消费总量意义重大。
鉴于组合预测模型的预测准确度较高,故而可以将其用于其它领域的研究。为了实现国家经济健康、稳定、可持续的发展,保护我们的生态环境和健康,我们应控制能源消费总量的过快增长。通过提高能源的利用率、开发可再生资源以及使用低碳能源等方法都可以减少能源的消耗。
致谢
本文在云南财经大学统计与数学学院石磊教授的指导和建议下,得以顺利完成,在此对石磊教授表示衷心的感谢!