1. 引言
洪水因暴雨形成,具有突发性,破坏性和危险性,可使村镇、城市及人民生命财产毁于一旦[1] 。陕北地区洪水灾害严重且频繁,修建水库和堤防等水利工程是必要的防洪措施。而推求设计洪水是防洪规划和建设的依据[2] [3] 。在水利工程中,往往需要推求大重现期的洪水设计值,而设计值可靠与否,会直接影响到工程的安危[4] -[6] 。目前,常用的参数估计方法有矩法、适线法、权函数法、概率权重矩法和线性矩法等,这些方法的估计精度及拟合效果优劣各异[7] [8] 。譬如,矩法有较大的估计偏差,尤其是对Cs的估计;概率权重矩法具有良好的不偏性,但对于Cs的抽样误差较大,尤其是短序列;权函数法提高了Cs的估计精度,但是权函数属于单参数估计,不能解决均值,特别是Cv的估计精度问题;国内通常采用适线法,其中图解适线法可灵活调整参数,但主观任意性较大,结果因人而异;这些方法在一定程度上改善了估计精度,但对于大洪水段设计值拟合效果稍差[9] 。因此,20世纪90年代,Bhattarai [10] [11] 建议使用部分线性矩(Partial L-Moments)来拟合分布,对于长序列洪水,该法以截取频率分布拟合大流量值,效果良好,使外延的大重现期设计洪水值精度得到提高,且借助于计算机,容易实现计算过程。
本文选用陕北地区7个水文站洪峰流量序列为例,以部分线性矩法进行洪水频率曲线拟合,进而评价所得洪水频率曲线对序列拟合效果及设计值误差,以期为该区水利建设提供计算依据。
2. 部分线性矩
部分线性矩是用于估计删失样本的参数估计方法。给定一个排序样本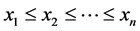 ,对于低删失,前4阶部分线性矩分别为
,对于低删失,前4阶部分线性矩分别为
 (1)
(1)
 (2)
(2)
 (3)
(3)
 (4)
(4)
其中,
 (5)
(5)
 (6)
(6)
式中, 为低删失门限值。
为低删失门限值。
3. 广义极值分布及其部分线性矩
广义极值分布(Generalized extreme value distribution, GEV)的分布函数为
 (7)
(7)
其逆函数形式为
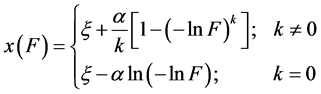 (8)
(8)
式中,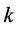 为形状参数,
为形状参数, 为尺度参数,
为尺度参数,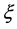 为位置参数。
为位置参数。
Wang (1990) [12] 提出了GEV分布部分概率权重矩,当 时,其表达式为
时,其表达式为
 (9)
(9)
式中,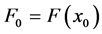 ,
, 为低删失门限值,
为低删失门限值, 为不完全gamma函数,即
为不完全gamma函数,即
 (10)
(10)
把r = 0, 1, 2代入式(9),可得
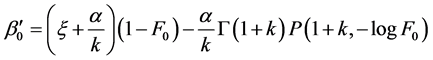 (11)
(11)
 (12)
(12)
 (13)
(13)
令上式左边为
 (14)
(14)
则有
 (15)
(15)
当 时,给定
时,给定 的取值范围
的取值范围 ,分别令
,分别令 ,根据式(15)分别计算各组取值对应的
,根据式(15)分别计算各组取值对应的 值,按式(16)拟合曲线,求得曲线拟合系数如表1所示。
值,按式(16)拟合曲线,求得曲线拟合系数如表1所示。
 (16)
(16)
Hosking [13] (1990)给出线性矩与概率权重矩的前4阶关系为
 (17)
(17)
 (18)
(18)
 (19)
(19)
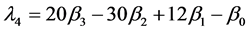 (20)
(20)
式中, 为概率权重矩,
为概率权重矩, 为前4阶线性矩,而部分概率权重矩与部分线性矩有类似的线性关系,式(14)中
为前4阶线性矩,而部分概率权重矩与部分线性矩有类似的线性关系,式(14)中 由
由 代替,并根据式(17)~式(20)的关系可得
代替,并根据式(17)~式(20)的关系可得
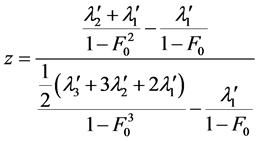 (21)
(21)
根据式(1)~式(3),由样本计算 ,并代入式(21),可得
,并代入式(21),可得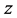 的估计量
的估计量 为
为
 (22)
(22)
上式计算出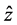 值,由式(16)计算参数
值,由式(16)计算参数 的估计值
的估计值 ,其系数由表1查算。式(11)和式(12)可得参数
,其系数由表1查算。式(11)和式(12)可得参数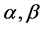 的估计值
的估计值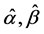 分别为
分别为
 (23)
(23)

Table 1. Coefficients, , , and for Equation (16)
表1. 不同 下式(16)的拟合系数
下式(16)的拟合系数
 (24)
(24)
当 时,部分线性矩转化为普通线性矩。Hosking [13] (1990)推出了GEV分布下普通线性矩为
时,部分线性矩转化为普通线性矩。Hosking [13] (1990)推出了GEV分布下普通线性矩为
 (25)
(25)
 (26)
(26)
 (27)
(27)
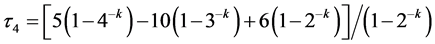 (28)
(28)
当 时,三个参数的估计量计算公式分别为
时,三个参数的估计量计算公式分别为
 (29)
(29)
式中, 。
。
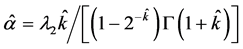 (30)
(30)
 (31)
(31)
式中, 可由样本进行计算。
可由样本进行计算。
4. 实例应用
本文选取陕北7个水文测站的年最大流量资料,经还原处理,资料满足一致性要求,研究GEV分布部分线性矩法应用于洪水序列拟合的效果,资料的基本情况如表2所示。
4.1. 绘制频率曲线
计算不同F0下各站年最大洪峰流量序列GEV分布参数估计值,由式(8)计算洪水设计值,并绘制理论频率曲线拟合图,如图1所示。
由图1看出,7个测站普通线性矩法(F0 = 0.0)对低尾部经验点据拟合结果较好,随着F0值的增大,洪水频率曲线对低尾部经验点据拟合结果变差,高尾部经验点据拟合结果得到显着改善,这表明部分线性矩法对高尾部洪水值拟合效果好。
4.2. 拟合效果分析
采用累积相对偏差平方和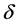 对上述拟合结果进行定量分析。式(32)为P = 50%~98%时,对应实测值与设计
对上述拟合结果进行定量分析。式(32)为P = 50%~98%时,对应实测值与设计

Table 2. Lengths of annual maximum flows
表2. 年最大流量资料系列长度

Table 3. Comparison of quantile errors using different F0
表3. 不同F0下各站设计值误差比较
值累积偏差平方和的计算公式。
 (32)
(32)
式中, 为实测值;
为实测值; 为设计值。计算结果如表3所示。
为设计值。计算结果如表3所示。
由表3可得出,与普通线性矩(F0 = 0.0)相比较,部分线性矩的设计值偏小。此外,除了张村驿站,其它6站随着F0的增大,高尾部设计值计算偏差越小,即频率曲线与高尾部(P > 50%)经验点据越来越接近,提高了设计值估算精度,这与图1拟合曲线结果相一致。而张村驿站,在F0 ≤ 0.4时,高尾部经验点据拟合效果与其它6站变化趋势相同,但F0 = 0.5时,设计值估算偏差变大,说明并非F0越大越好,即并非截掉小洪水值越多越好,而是选择合适的F0值,可提高设计值估算精度。因此,通过增大F0值的方式来拟合高尾部洪水值是可行的,提高了该区设计值估算精度。
5. 结论
本文以陕北地区7个水文测站的年最大洪峰流量序列为例,以部分线性矩法对洪峰序列进行参数估计,评价其拟合效果及设计值的偏差。结果表明,部分线性矩法通过增大F0值的方式来拟合高尾部洪水值是可行的,且随着F0的增大,高尾部设计值计算偏差越小,可为研究区防洪工程建设提供理论依据。但并非F0越大越好,应选择合适的F0值,可提高设计值估算精度。