1. 引言
纤维金属层板(Fiber Metal Laminates，简称FMLs)是一种由金属薄板和纤维增强复合材料交替铺设后，在一定温度和压力下固化而成的一种层间混杂复合材料[1] -[6] ，其典型结构如图1所示 [7] 。纤维金属层板综合了传统纤维复合材料和金属材料的优点，克服了单一复合材料和金属材料的不足，不但具有高比刚度和比强度，还具有优良的疲劳和损伤容限性能[8] [9] ，其最突出的特点是在恒幅载荷下能够保持相对恒定的裂纹扩展速率[10] -[13] 。芳纶铝合金层板(ARALL)和玻璃纤维铝合金层板(GLARE)是目前国际上比较成熟的两类纤维金属层板产品[14] [15] ，主要用于飞机机身结构[16] [17] 。作为大型飞机主承力结构备用新型材料，纤维金属层板具有良好的发展前景。
由于纤维金属层板在疲劳过程中的损伤行为较为复杂，既有金属层内的裂纹扩展，又有层间的分层扩展，两者相互耦合，相互影响，使得层板的裂纹扩展与寿命预测变得十分复杂。本文综述了纤维金属层板疲劳裂纹扩展行为的相关研究及预测方法。在本文的第二部分，介绍了纤维金属层板的疲劳损伤机制，第三部分则介绍了恒幅载荷下纤维金属层板的疲劳裂纹扩展速率预测方法，第四部分将介绍变幅载荷下纤维金属层板的疲劳裂纹扩展及分层行为研究。
2. 纤维金属层板的疲劳损伤机制
纤维金属层板在疲劳过程中伴随两种损伤模式：金属层的疲劳裂纹扩展和金属/纤维界面的分层扩展 [18] 。典型纤维金属层板的疲劳裂纹扩展和分层机制如图2所示 [19] 。
疲劳裂纹在纤维金属层板的金属层中扩展时预浸料层中的纤维不产生断裂，此时纤维会通过胶接作用阻碍裂纹尖端张开，裂纹区域金属层本应承载的部分载荷转移到预浸料层中，这部分转移的载荷称为桥接应力[20] [21] 。桥接应力降低了裂纹尖端的有效应力强度因子幅(ΔKeff)，从而减缓裂纹扩展速率。与此同时，桥接应力也会使金属层与预浸料层间产生剪切变形，从而导致分层，分层将降低桥接应力效力 [22] - [25] 。当纤维金属层板经过一定的疲劳循环次数后，裂纹扩展和分层扩展进入平衡稳定状态，此时疲劳裂纹将以近似恒定的速率扩展 [26] - [28] 。
Figure 1. The typical sketch of the 3/2 lay/up FMLs [7]
图1. 纤维金属层板典型3/2结构示意图 [7]
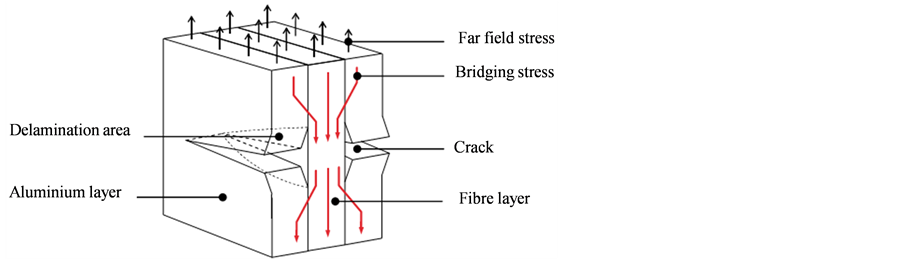
Figure 2. Typical fatigue crack growth and delamination mechanism of FMLs [19]
图2. 典型纤维金属层板疲劳裂纹扩展和分层机制 [19]
3. 恒幅载荷下纤维金属层板的疲劳裂纹扩展行为预测模型
3.1. 唯象模型
唯象模型主要包括应力强度修正因子βFML、柔度法、裂纹张开位移和桥接应力的线性关系、裂纹扩展速率和有效应力的关系、等效裂纹长度l0等理论。
Toi [29] 最早提出了应力强度修正因子βFML理论。他将纤维金属层板看成一个统一的金属结构，认为GLARE层板的所有疲劳特性都可以由修正因子βFML计算得到，并给出：
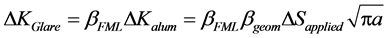(1)
其中，βgeom是几何修正因子。并且，Toi认为修正因子βFML只是裂纹长度a的函数：
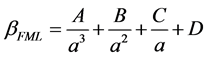(2)
这一观点一经提出便得到了质疑，一些学者[30] [31] 指出βFML不仅与裂纹长度有关，还取决于施加载荷，裂纹形态等多种因素。Takamatsu等人[32] [33] 通过试验证明βFML与应力水平有较大关系，因此对式(2)进行了修正：
(3)
修正后的公式仍然具有很大的局限性，Alderliesten [30] 强调层板的铺层结构、层板各层的残余应力以及初始锯切切口长度等都应被考虑在内。并且，无论是Toi模型还是修正后的Takamatsu模型都很难将其实际应用于纤维金属层板，这是由于修正因子βFML理论的前提是将纤维金属层板看作一个统一的金属结构，而实际上并非如此。
Cox [34] 提出了两种经验方法，一种是他假定桥接应力与裂纹张开位移之间是线性关系；另一种是认为裂纹扩展速率与施加的应力之间的关系为：
(4)
其中，Δσa为所施加的远程应力幅，fs是唯一的材料特征函数。在对Toi模型的讨论中已经指出，纤维金属层板的裂纹扩展行为是由很多参数共同决定的，无法仅用一个函数fs来描述。
郭亚军和吴学仁 [35] [36] 以纤维金属层板疲劳裂纹稳定扩展的特性为基础，提出了等效裂纹长度l0的概念。根据裂纹扩展速率方程，层板经过一定的循环次数后，其有效应力强度因子幅值ΔKeff为常数:
(5)
其中ΔS为远程应力幅。由于ΔKeff在疲劳过程中为常数，所以l0 (即等效裂纹长度)在疲劳过程中保持不变：
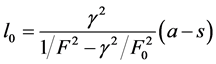(6)
式中F为裂纹构形因子；γ为层板的归一化有效应力强度因子幅(层板内铝合金层感受到的应力强度因子幅ΔKeff与远程应力强度因子幅ΔK之比)，可由试验中测得的疲劳裂纹扩展速率反推求得，即：
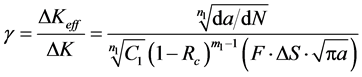(7)
该模型不需要计算层板的桥接应力，也不需要研究层板的分层扩展，而是从纤维金属层板裂纹稳定扩展的特性出发建立的。而略显不足的是，对每种不同级别和铺层的GLARE层板，l0都要分别确定 [30] 。
唯象模型都是解析运算，计算工作量小，它的提出使得纤维金属层板的疲劳裂纹扩展速率与寿命预测变得跟金属材料一样方便。然而，唯象模型的简单运算并不能很好地反映出纤维金属层板疲劳过程中的复杂机制。
3.2. 基于断裂力学的分析模型
较为典型的基于断裂力学的分析模型有Marissen模型 [37] (1988年)、郭—吴模型 [38] (1998年)和Alderliesten模型 [39] (2007年)。
1988年，Marissen [37] 发展了一种二维分析方法来描述和预测ARALL层板的疲劳裂纹扩展行为，他主要从层板的分层扩展和胶粘剂的剪切变形两方面研究。该模型利用Paris公式来描述ARALL层板的疲劳裂纹扩展行为，并且认为外层铝合金板裂纹尖端的有效应力强度因子与裂纹张开位移直接相关：
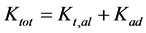(8)
其中，Kt,al是由外层铝合金板的远程加载应力和固化过程中产生的残余应力共同决定的应力强度因子：
(9)
Kad是由胶粘剂剪切变形引起的应力强度因子：
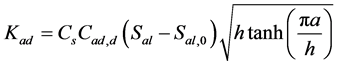(10)
式中的Cd、Cs和Cad,d分别为裂纹桥接分层、锯切尺寸和胶粘剂剪切变形的修正因子，h为材料性能参数，Sal,0是应力强度因子为0时的远程加载应力。同时，Marissen选用能量释放率描述分层扩展，分层扩展速率db/dN与能量释放率G的关系为：
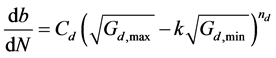(11)
式中，Cd，nd，k均为材料性能常数。
为简化模型便于分析计算，Marissen假设分层形状和裂纹张开形状都是椭圆形，但在GLARE层板中该假设不成立 [40] [41] 。对于ARALL层板，芳纶纤维与铝合金板之间具有一定厚度的胶粘剂层，然而GLARE层板中玻璃纤维与铝合金板之间并没有该胶粘剂层 [42] ，因此，Marissen模型并不适用于GLARE层板。
1998年，郭亚军和吴学仁 [38] 在Marissen模型的基础上发展了应用于GLARE层板的疲劳裂纹扩展预测模型。他们由裂纹张开位移推导出桥接应力关系：
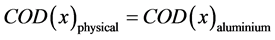(12)
其中COD(x)physical由桥接纤维的变形、分层前沿胶粘剂的剪切变形和分层区域内金属薄板的变形构成；而COD(x)aluminium由远程应力引起的裂纹张开位移和桥接应力引起的裂纹张开位移构成。由远程应力σ0引起的裂纹张开位移u∞(xi)可表示为：
(13)
式中，Ela为层板纤维方向的弹性模量，w为试样宽度。将桥接区划分为N个单元杆，第j个杆单元宽度为2wj，中心点坐标为xj，作用在此单元的桥接应力用均匀应力σbr,j表示(相对于整个层板厚度，见图3 [15] )。对于中心裂纹试样，由桥接应力引起的xj处的裂纹张开位移ubr(xi)可表示为：
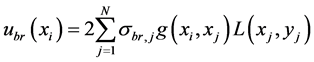(14)
其中，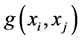
表示第j个杆单元的桥接应力σbr,j对xi处裂纹张开位移的权函数，
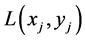将桥接应力对分层边界的作用考虑在内。由此，式(12)经过推导得到桥接应力分布控制方程：
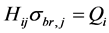(15)
(16)
(17)
式中，Pi + D、δij、gijLj分别代表桥接纤维伸长、胶粘剂的剪切变形和桥接应力引起的裂纹张开位移。
基于该模型的参数分析表明，影响桥接应力分布的主要因素为分层形状与尺寸以及初始锯切裂纹长度。郭亚军和吴学仁通过大量试验观察，发现GLARE层板疲劳裂纹扩展过程中的分层形状不是椭圆形，而是更接近于三角形，故在其模型计算中假设分层形状为三角形。郭亚军和吴学仁提出的纤维桥接应力分布的计算模型建立在更一般的概念之上，理论基础坚实，计算精度高，是对Marissen模型的实质性改进和发展。
在分层扩展方面，郭亚军和吴学仁沿用了Marissen模型中类似式(11)的关系。不同的是，舍弃了式(11)中的系数k，只保留Cd和nd两个系数。这是由于对ARALL层板k = 0.69，而对GLARE层板k = 1。
在计算裂纹扩展速率时，郭亚军和吴学仁选用了Walker方程表征扩展速率：
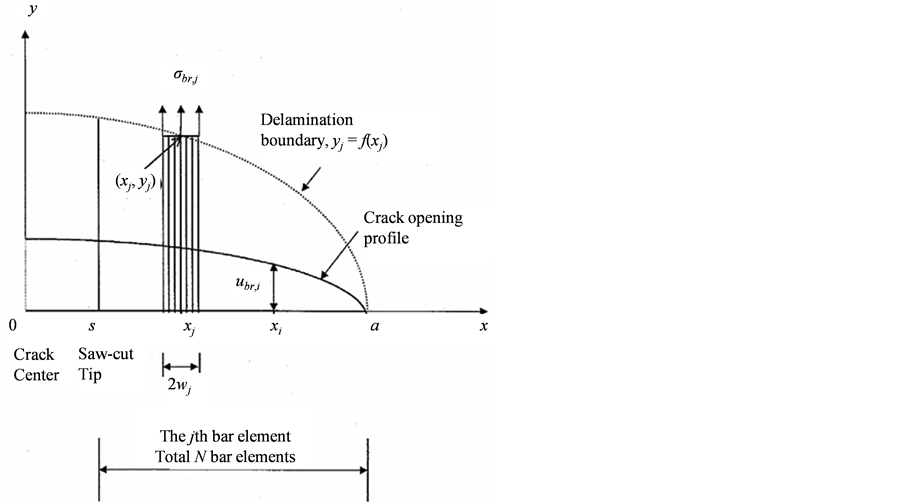
Figure 3. The crack opening displacement induced by bridging stress [15]
图3. 桥接应力引起的裂纹张开位移 [15]
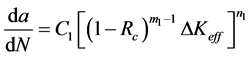(18)
式中，C1、m1、n1是试验常数；Rc为考虑残余应力影响后的有效应力比。有效应力强度因子(Keff)采用权函数方法计算，即：
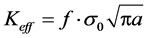(19)
式中，f是无量纲应力强度因子，可用权函数方法求解 [43] 。
在总结前人经验的基上，Alderliesten [39] 针对GLARE层板发展了一种新的基于断裂力学的分析模型。大量研究表明 [41] [44] - [46] ，实际的分层形状既不是三角形也不是椭圆形。因此，在计算桥接应力过程中，Alderliesten并没有假设分层形状为椭圆形或三角形，而是将其定义为任意连续形状。实际的分层形状由试验获得的分层扩展性能和裂纹区域真实桥接应力共同决定。
Alderliesten模型中裂纹张开位移关系与郭—吴模型相似，即：
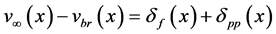(20)
式中，v∞(x)为远程应力造成的裂纹面张开位移；vbr(x)为桥接应力造成的裂纹面张开位移；δf(x)为纤维伸长量；δpp(x)为预浸料层变形量。其不同之处在于，在沿胶粘剂的剪切变形计算中，Alderliesten认为该剪切变形应表征为整个预浸料层的剪切变形，并推导出了相关计算公式 [39] 。
根据叠加原理，Alderliesten模型认为裂纹尖端的有效应力强度因子是由远程应力和桥接应力共同作用的：
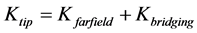(21)
得到有效应力强度因子后，可采用Paris经验公式来表达裂纹扩展速率。
不必规定分层为某一固定形状，而是通过力学模型分析获得，这是Alderliesten模型最大的创新点。
除了以上三种预测模型外，还有很多研究者针对纤维金属层板开展了大量的疲劳裂纹扩展试验并发展了多种基于断裂力学的分析模型 [47] - [54] 。
3.3. 有限元模型
相比以上两类模型，有限元模型的发展还处于初级阶段。目前比较具有代表性用来预测纤维金属层板疲劳裂纹扩展行为的有限元模型有Yeh的二维有限元模型 [55] [56] 和Burianek的全局–局部有限元模型 [57] 。
Yeh [55] [56] 针对ARALL层板进行分析研究，建立了一个二维有限元模型。模型是由铝合金层的四节点平面应力元和纤维层的二节点桁架单元组成，二者之间用特殊界面单元连接。Yeh指出，这一模型仅适用于拉伸疲劳载荷，对于有压应力存在的情况不适用。
Burianek [57] 研究了一种三维多级全局–局部有限元模型来预测钛-碳层板的疲劳裂纹扩展速率。与二维有限元模型相比，Burianek认为三维有限元模型考虑了平面应力和平面应变状态，因此比二维模型更为精确。
Alderliesten [42] 对现有的预测模型进行了对比分析，他认为，唯象模型存在局限性和不精确性，而有限元模型的发展仅处于初级阶段。相比之下，基于断裂力学的分析模型精度更高，理论基础更扎实。因此，在纤维金属层板疲劳裂纹扩展预测模型中，基于断裂力学的分析模型是主流。
4. 变幅载荷下纤维金属层板的疲劳裂纹扩展及分层行为研究
实际上，飞机在实际服役过程中多承受变幅载荷，因此变幅载荷下疲劳裂纹扩展行为分析是损伤容限研究的关键。材料在恒幅和变幅载荷下疲劳裂纹扩展行为的主要区别是在变幅载荷下存在交互作用。由于纤维金属层板在疲劳裂纹扩展过程中存在桥接应力，因此在变幅载荷下，可能会存在桥接效应与过载效应(或负载效应)之间的交互作用，二者相互影响，使得变幅载荷下纤维金属层板的疲劳裂纹扩展行为研究变得更加复杂。
Plokker等人 [58] 研究了GLARE3-4/3-0.3层板在多种变幅载荷下的疲劳裂纹扩展行为，并且将线性损伤累计模型的预测结果与试验结果进行对比。试验证明，在过载条件下GLARE层板表现出和金属材料相似的迟滞行为。但由于桥接应力的存在，这一迟滞效应较金属材料要小一些。因此，过载后不考虑交互作用的线性损伤累积模型与实际结果不吻合。另外，GLARE层板的迟滞效应同过载比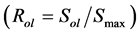
成正比。然而，压缩过载却并没有产生裂纹扩展加速效应，这是由于没有发生断裂的纤维层占据了绝大部分载荷，使得本来就不明显的加速效应进一步减小以致无法观测到。
Woerden [59] 对GLARE3-3/2-0.3层板在不同单峰过载条件下的疲劳裂纹扩展速率进行了试验研究。结果表明，过载后GLARE层板的迟滞阶段随着过载施加时裂纹长度(aol)的增加而增大。这是因为过载裂纹长度的增加使得裂纹尖端应力强度因子增大，从而导致了裂纹尖端塑性区的增大。
Khan等人 [60] 对Wheeler模型进行了修正，将其用来预测GLARE层板在变幅载荷下的疲劳裂纹扩展速率。原始Wheeler模型利用Paris方程来计算裂纹扩展速率：
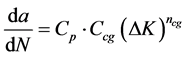(22)
式中，Cp为迟滞系数，Ccg和ncg为Paris公式拟合系数。由于Paris方程依赖于应力比而存在，因此，为了将应力比的影响考虑在方程内，Khan使用Schijve方程 [61] (式(23))来修正Wheeler模型，
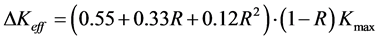(23)
得到的GLARE层板在变幅载荷下的疲劳裂纹扩展速率方程为：
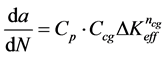(24)
该模型在一般过载情况下能进行较为准确的预测。但是，当由于大量过载循环产生了较大的裂纹尖端塑性区时，预测结果与试验结果相差较大。对于飞机谱来说，陡谱的预测结果能与试验结果较好的吻合，但是对于平谱却并不适用，如图4所示 [60] ，这可能是由于频繁的过载导致裂纹尖端被抑制。
此外，Khan [62] 还验证了CORPUS模型对GLARE层板的适用性。与修正后的Wheeler模型相比，在一般变幅载荷下，CORPUS模型的预测结果与试验结果更为接近，但对飞机谱的预测结果却与试验结果相差很远。
在分层扩展方面，Khan等人 [63] 采用双面搭接剪切(DCLS)试样研究了GLARE层板在过载情况下的分层扩展速率。结果表明，分层扩展在变幅载荷下不存在交互作用，即分层扩展速率仅取决于当前状态下的应力水平，而与载荷施加的顺序无关。Khan还使用扫描电镜(SEM)观测了分层界面处的金属表面和纤维表面。他发现，在分层金属表面则能观测到一个个规则排列的条纹(见图5 [63] )。由于这些条纹的产生是由分层导致的，因此条纹间距代表分层扩展速率。而这些条纹的间距仅与当前应力水平有关，在低载处条纹间距较小，在高载处条纹间距较大。由此可以进一步验证过载不会对分层扩展产生交互作用。
另外，吴学仁和郭亚军 [64] 的研究也证明，GLARE层板在变幅载荷下的分层扩展速率计算仍可采用恒幅下的分层扩展方程。
Alderliesten [65] 和Khan等人 [66] 分别对GLARE3-3/2-0.3和GLARE3-5/4-0.4层板在疲劳裂纹扩展过程中的分层形状与尺寸进行了研究。在两者的研究中，过载都对GLARE层板的分层形状产生了显著影响，即在过载位置附近分层形状发生了弯折。这一现象可从试验结束后的腐蚀去层形貌照片中看出，见图6 [66] 。
Alderliesten把这一现象归因于过载塑性导致了应力的重新分布，而Khan则认为过载导致的裂纹扩展迟滞是分层形状改变的主要原因。Khan提出的分层形状变化机制见图7 [66] 。施加过载(或高低载转换)
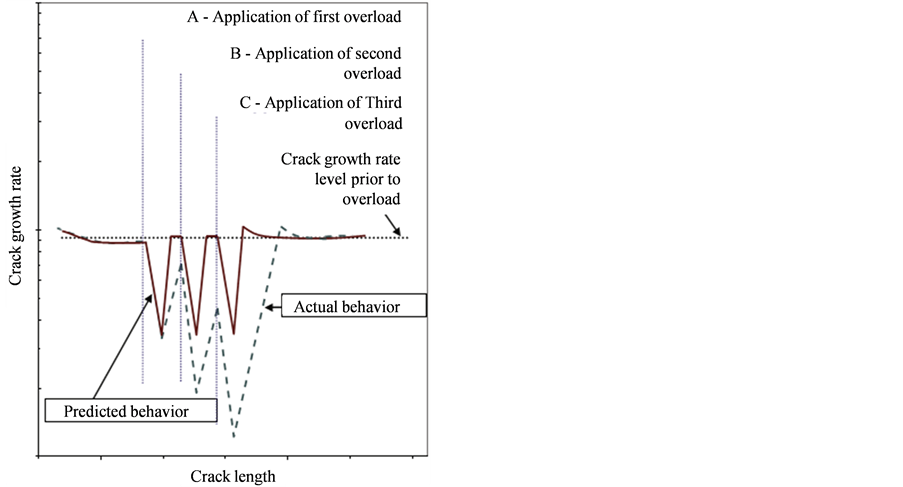
Figure 4. The difference of prediction model and test result under flat spectrum [60]
图4. 平谱下预测模型与试验结果差异示意图 [60]
Figure 5. The marks of delamination growth of LO load (a) and HI load (b) [63]
图5. 低载(a)和高载(b)处的分层扩展标记(条纹) [63]
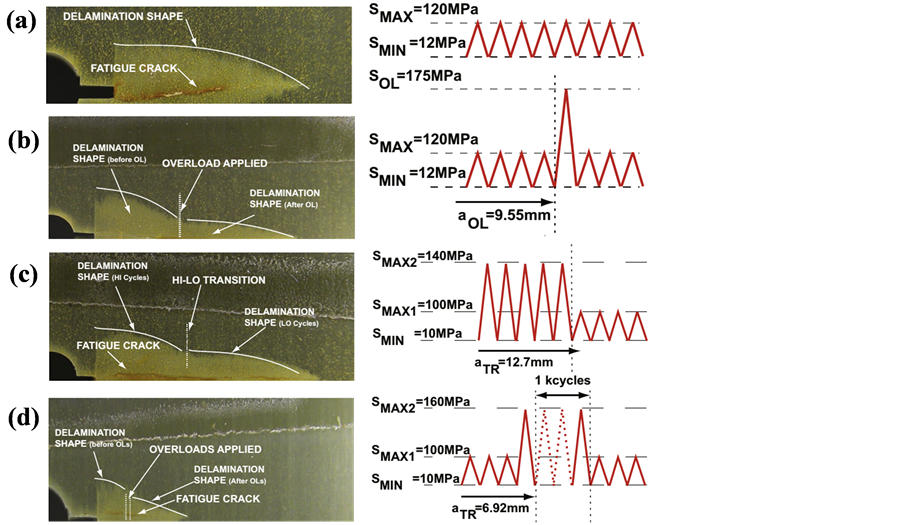
Figure 6. The delamination images under different load conditions: (a) constant amplitude load; (b) Single overload; (c) High-low block load; (d) Multiple overload [66]
图6. 不同加载条件下的分层形貌 [66] 。(a) 恒幅；(b) 单峰过载；(c) 高低过载；(d) 多峰过载
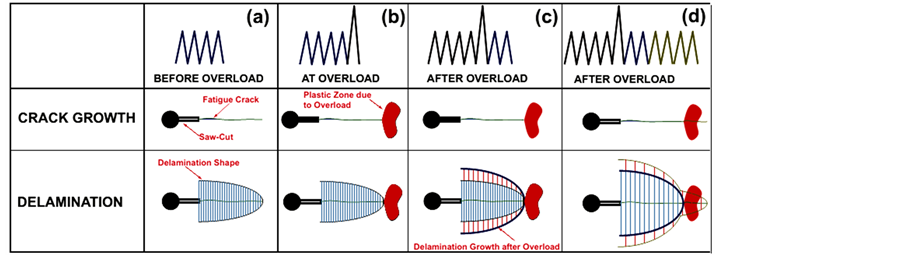
Figure 7. The changing mechanism of delamination shapes before and after overload [66]
图7. 过载前后分层形状的变化机制 [66]
后，由于过载塑性区分产生使得裂纹扩展发生迟滞(图7(b))；由Khan之前的分层研究 [63] 表明，分层扩展不存在过载交互作用，因此，在裂纹扩展迟滞期间，尽管在裂纹延伸方向上的分层扩展受到抑制，但在载荷施加的方向分层会继续扩展(图7(c))；当裂纹尖端扩出过载塑性区后，裂纹扩展速率恢复正常水平，此时，分层重新开始在裂纹延伸方向和载荷施加方向同时扩展(图7(d))。这样，在过载施加的位置附近便产生了弯折。
Khan的这一理论较好地解释了裂纹扩展迟滞效应给分层形状带来的影响。在建立过载条件下GLARE层板的疲劳裂纹扩展模型时，如果能将过载塑性导致的应力重新分布这一因素考虑在内，将会在一定程度上提高预测精度。
5. 结语
纤维金属层板是一种层间混杂复合材料，它综合了单一金属材料和纤维复合材料的优点，具有优良的疲劳性能，是大型飞机主承力结构备用新型材料。纤维金属层板的疲劳损伤机制较为复杂，国内外学者对此进行了大量的研究，建立了多种恒幅载荷下的疲劳裂纹扩展行为预测模型，为纤维金属层板的损伤容限设计和疲劳寿命预测提供了理论依据。由于飞机在服役过程中多承受变幅载荷，因此变幅载荷下的相关研究更具有实际意义。然而，相比恒幅载荷，变幅载荷下纤维金属层板的疲劳裂纹扩展行为机制研究明显不足，相关预测方法的研究还处于初级阶段。由于变幅载荷下，过载迟滞效应与纤维桥接效应之间产生了交互作用，使得裂纹扩展机制更加复杂，预测难度更大。随着纤维金属层板疲劳裂纹行为的进一步研究，相信其在实际应用中将发挥越来越重要的作用。
基金项目
工信部民机科研专项课题“民用飞机新型轻质结构设计、分析和综合验证技术研究”。