1. 引言与预备知识
FTS最早出现在20世纪50年代俄罗斯文献中,随后在60年代出现在西方控制文献中[1] [2] 。
一般来说,研究有限时间稳定性可以从2个方面考虑
1) 预先给定了状态变量的界,寻求最长的时间区间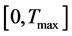 。
。
2) 预先给定一段有限的时间区间 ,寻求最小的状态变量的界,使在
,寻求最小的状态变量的界,使在 上有限时间稳定。
上有限时间稳定。
Lyapunov稳定性是在采用状态空间描述以后,初始条件作用下系统方程的解是否具有收敛性。
应当指出的是有限时间稳定(FTS)和Lyapunov稳定是2个不同的概念。一个系统可以是FTS的,但不是Lyapunov渐近稳定的,反之亦然。
有限时间稳定(FTS)和Lyapunov稳定的区别主要体现在以下几点
1) Lyapunov渐近稳和FTS考虑的时间长短不同。
2) Lyapunov渐近稳定和FTS对边界的要求不同。
3) Lyapunov渐近稳定和FTS,前者考虑的是系统的稳态行为,后者考虑的是系统的暂态行为。
最近,不同系统的有限时间稳定性吸引了很多学者的注意,[3] -[15] 给出了线性系统和线性时变系统的有限时间稳定的充分必要条件,[16] 讨论了线性脉冲系统的有限时间稳定性。
考虑到大部分文献给出的系统是有限时间稳定的判定条件是借助于Lyapunov函数,但是这个函数是很难构造的,这促使我们思考,有没有其他的方法可以考虑,本文通过求解微分方程组,把脉冲切换系统的解解出来,使得系统的解只要满足一些条件就可以保证系统是有限时间稳定的。
切换系统可以用下面的方程表示
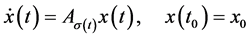 (1)
(1)
状态变量 ,切换信号
,切换信号 ,
, 是一系列描述子系统的常数实矩阵。我们假定
是一系列描述子系统的常数实矩阵。我们假定 是不稳定的,
是不稳定的,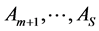 是稳定的。
是稳定的。
对应切换信号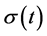 ,我们有下面的切换子序列
,我们有下面的切换子序列
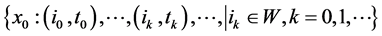
当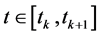 时,第
时,第 个子系统被激活。
个子系统被激活。
定义1 (平均停留时间)
对任意的正标量 ,
,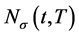 表示切
表示切 在
在 上切换次数,若
上切换次数,若
 (2)
(2)
则 称为平均停留时间。
称为平均停留时间。
不失一般性,这里仍然假定 是不稳定的,
是不稳定的,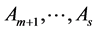 是Hurwitz稳定的,可以证明存在一系列正数
是Hurwitz稳定的,可以证明存在一系列正数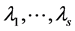 ,保证
,保证 是Hurwitz稳定的。并且应用代数矩阵理论,得到
是Hurwitz稳定的。并且应用代数矩阵理论,得到

 (3)
(3)
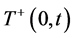 表示所有不稳定子系统的激活时间的总和,
表示所有不稳定子系统的激活时间的总和, 表示所有Hurwitz稳定子系统的激活时间的总和。
表示所有Hurwitz稳定子系统的激活时间的总和。
定义
任意选择一个标量 满足切换规则
满足切换规则
 (4)
(4)
定义2
如果矩阵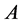 的非对角线元素是非负的,称
的非对角线元素是非负的,称 为Metzler矩阵。
为Metzler矩阵。
定义3
若矩阵 的最大特征值
的最大特征值 ,称
,称 为Hurwitz矩阵。
为Hurwitz矩阵。
定义4
一个系统被称为正系统,如果初始时刻 ,则
,则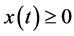 ,
, 。
。
定义5
系统(1)被称为正系统,当且仅当矩阵A的非对角线元素是非负的,即A为Metzler矩阵。
2. 正脉冲切换系统的有限时间稳定性
考虑下面的连续时间的正脉冲切换系统

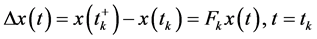 (5)
(5)
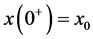
其中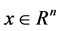 是系统的状态变量,
是系统的状态变量, 是初始时刻的值,
是初始时刻的值, 是切换信号并且是分段连续常值函数,
是切换信号并且是分段连续常值函数, 表示子系统的切换个数,
表示子系统的切换个数, 是常数矩阵,
是常数矩阵, ,
, 是常数矩阵,表示系统在切换时刻的脉冲影响,
是常数矩阵,表示系统在切换时刻的脉冲影响, 。
。
定义6
给定3个正数 ,并且满足
,并且满足 ,
,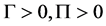 表示正无限维矩阵,
表示正无限维矩阵, 表示切换信号,若下式成立。
表示切换信号,若下式成立。

则系统(5)对任意的 是有限时间稳定的。
是有限时间稳定的。
定义7
对于给定的切换信号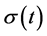 ,假定脉冲切换系统对
,假定脉冲切换系统对 有限时间稳定,如果存在正数
有限时间稳定,如果存在正数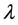 ,满足对于所有的
,满足对于所有的 ,
, 为已知常数
为已知常数

称 为脉冲切换系统有限时间稳定的度。
为脉冲切换系统有限时间稳定的度。
定理1
给定 ,若切换信号满足上式,并且
,若切换信号满足上式,并且

那么存在一个正的常数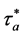 ,保证系统(5)是在任意的平均停留时间下是有限时间稳定
,保证系统(5)是在任意的平均停留时间下是有限时间稳定

证明: 表示切换时刻,
表示切换时刻, 在
在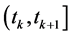 上的值用
上的值用 表示,
表示,
当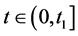 ,应用常微分方程理论,解得
,应用常微分方程理论,解得
在切换时刻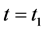 ,
,

当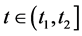 ,可得
,可得

依次类推,得到当 时,系统切换次数
时,系统切换次数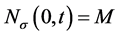
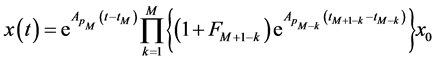
由(3)式,和 ,
,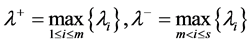 ,上式变为
,上式变为
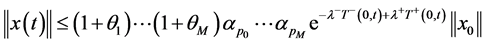
取 ,得到
,得到

对于给定的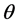 和
和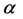 ,一定存在一个有限的常数k,满足
,一定存在一个有限的常数k,满足
因此,又得到下面的式子

由(4)式,

如果取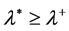 ,即使所有的子系统是不稳定的,即
,即使所有的子系统是不稳定的,即 ,上述等式也成
,上述等式也成
立,得到
 (6)
(6)
又因为一定存在一个常数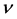 ,满足
,满足

且 表示在
表示在 上切换次数,所以
上切换次数,所以
 ,
, ,得到
,得到
 (7)
(7)
 (8)
(8)
 (9)
(9)
结合(6),(7),(8),(9)式,得
 (10)
(10)
又因为
 (11)
(11)
结合(10),(11)式,得
则系统(5)是在任意的平均停留时间下是有限时间稳定的。
3. 总结与展望
大部分文献给出的结论都是通过构造Lyapunov函数去证明系统的有限时间稳定,而Lyapunov函数不容易构造。本文从解的存在性入手,即用求解微分方程组的方法,系统的解若满足一些条件,即可证明系统的稳定性,最后,把结果推广到连续时间的脉冲切换系统的稳定性问题上。
有限时间稳定在实际应用和理论研究中有很大的价值,所以吸引了许多学者的关注,但是现在存在的结果比较保守,而且大部分是充分条件,即使给出的是必要条件,这些结果都有很大的局限性,并不能解决所有问题,这促使我们继续研究,本文可以从以下几个个方面继续讨论。
1) 研究带有时滞的脉冲切换系统的有限时间稳定。
2) 把构造解的方法推广到更复杂的混杂系统中。
基金项目
中国自然科学基金:11261033。