1. 引言
蔬菜和水果能为人体提供丰富的矿物质,维生素和膳食纤维等人体所需的营养元素。近年来,在中国,居民消费水平不断提高,人们对营养均衡的意识也有所增强。但是,多年以来养成的喜食、饱食、偏食等习惯尚未根本扭转,导致了我国的果蔬消费近乎盲目无序,进一步影响到了果蔬生产。因此,预测我国果蔬的消费与生产趋势具有重要的意义。
近几年来,这方面的文章也越来越多,文献 [1] 告诉我们每日应吃果蔬的种类及相应的数量,对如何实现人体营养均衡进行具体指导;文献 [2] 主要分析了蔬菜消费的现状,通过主成分分析法分析出影响中蔬菜消费的五个因素,再利用回归方程得出人均蔬菜消费量的模型;文献 [3] 将年人均蔬菜消费量序列转化为不同的状态和状态的转移概率,用Markov链遍历性原理,得到经过长期变化之后年增减率的数学期望,对我国居民年人均蔬菜消费量趋势进行了分析;文献 [4] 运用主成分分析的方法,建立我国蔬菜总产的主成分回归预测模型,并对中国未来几年的蔬菜总产作出预测,为国家宏观决策者提供一些有价值的参考数据。
由于蔬菜和水果的种植受到各种元素的制约,要满足人体对于营养元素的合理摄入量,还要使种植者尽量获得较大利益;而且,作为国家宏观战略,还要考虑土地面积等其他因素。基于这些原因,在本文,建立食饵–捕食者模型,来预测未来几年果蔬的产量和消费量,根据结论给出到2020年我国果蔬生产的战略调整建议。
2. 模型假设
1) 忽略人的年龄结构和个体差异等因素;
2) 假设不存在时滞因素,如果消费量对果蔬的反馈调节作用即刻实现,即果蔬进入人体后立即被人体吸收等;
3) 果蔬进入人体后被完全吸收,不考虑人体代谢等因素的影响,即消费量等于人体吸收量;
4) 假设人与果蔬属于都不可以独立生存但又相互依赖的关系,即果蔬为人体提供必需的营养成分,所以人不能离开果蔬而独立存在;而对于果蔬,其来源于种植者的种植,来满足人自身的营养需求,当人不存在时,果蔬也就不复存在;
5) 影响果蔬消费量的因素中,果蔬价格、土地面积、营养成分三者之间互不干扰;
6) 忽略其他无关因素影响。
3. 符号说明
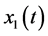 ——甲种群在
——甲种群在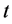 时刻的数量;
时刻的数量;
 ——乙种群在
——乙种群在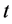 时刻的数量;
时刻的数量;
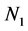 ——甲种群的环境最大容纳量;
——甲种群的环境最大容纳量;
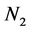 ——乙种群的环境最大容纳量;
——乙种群的环境最大容纳量;
 ——甲种群的固有增长率;
——甲种群的固有增长率;
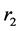 ——乙种群的固有增长率;
——乙种群的固有增长率;
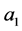 ——单位数量的乙在果蔬的价格、土地面积、营养成分等因素的影响下对果蔬的需求量为单位数量甲消耗的
——单位数量的乙在果蔬的价格、土地面积、营养成分等因素的影响下对果蔬的需求量为单位数量甲消耗的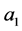 倍;
倍;
 ——单位数量乙提供的供养甲的食物量为单位数量甲消耗的供养甲食物量的
——单位数量乙提供的供养甲的食物量为单位数量甲消耗的供养甲食物量的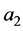 倍;
倍;
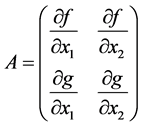 ——系统的线性化矩阵;
——系统的线性化矩阵;
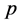 ——表示矩阵
——表示矩阵 的特征根之和的相反数;
的特征根之和的相反数;
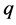 ——表示矩阵
——表示矩阵 的特征根之积。
的特征根之积。
4. 建立模型
首先运用Spss软件,对水果和蔬菜的营养素数据进行标准化处理类似于文献 [2] 的做法,分别对两组数据进行主成分分析,搜索出近几年相关水果和蔬菜的产量,并结合文献 [4] [5] 中相关果蔬产量,筛选出合适的研究对象。
果蔬可以看做人的食饵,记作甲种群(打包处理,不区分生物学意义上种群的定义);人作为捕食者,记作乙种群。这样果蔬与人构成食饵—捕食者模型。参考文献 [6] 中的模型,由于消费量与人成正比例关系(忽略人的年龄结构和个体差异等因素),因此消费量可以对应于人的数量。由于环境资源有限,存在人的环境最大容纳量;由于土地资源的分布和面积等因素,亦存在果蔬的环境最大容纳量。
在实际问题中,由于果蔬为人体提供必需的营养成分,所以人不能离开果蔬而独立存在;而对于果蔬,其主要来源于种植者的种植来满足人的自身需求,当人不存在时,果蔬也就不复存在。因此,甲乙两个种群属于都不可以独自生存的相互依存关系。由于甲为乙提供食物促进乙的增长,对应于消费量的增长;消费量的变化又通过供求关系等因素反馈调节果蔬生产的数量(如图1)。
对于种群乙:
由于种群乙没有甲的存在会死亡,则乙单独存活时有:
 (1)
(1)
甲为乙提供食物,于是(1)右端应该加上甲对乙的增长的促进作用,有
 (2)
(2)
显然,仅当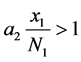 时种群乙的数量才会增长。与此同时,乙的增长又会受到自身的阻滞作用(当生
时种群乙的数量才会增长。与此同时,乙的增长又会受到自身的阻滞作用(当生
产量增长时,种植面积会增加,生产量会受到土地面积等因素制约)。所以(2)右端还应加上logistic项,

Figure 1. The diagram of population a and b
图1. 甲、乙种群关系图
方程变为:
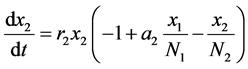 (3)
(3)
对于种群甲:
由于种群甲不能单独生存,则甲单独生存时有
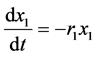 (4)
(4)
乙通过人对甲有调节的作用,于是(4)式应加上对甲的增长的调节作用,有
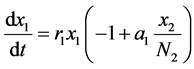 (5)
(5)
显然,仅当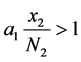 时种群甲的数量才会增长,与此同时甲的增长又会受到自身的阻滞作用(人口增
时种群甲的数量才会增长,与此同时甲的增长又会受到自身的阻滞作用(人口增
长时会受环境承载力等因素的制约,自然资源、环境条件等会对人口增长起阻滞作用,使人口增长率下降)。所以(5)右端还应加上logistic项,方程变为
 (6)
(6)
综合(3),(6)可得
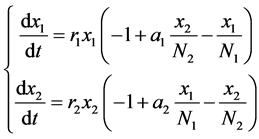 (7)
(7)
我们先求解模型方程的平衡点,并讨论其稳定性,从而对两种群的变化趋势作出判断。
由
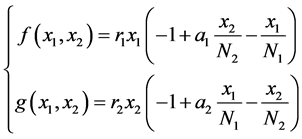 (8)
(8)
易得以下四个平衡点:
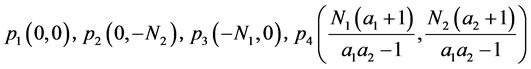
系统(8)的线性化矩阵为:
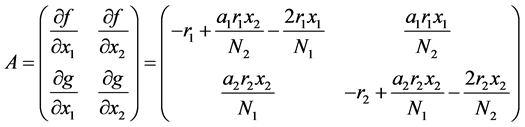
下面讨论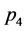 点的稳定性,其他点类似讨论。将
点的稳定性,其他点类似讨论。将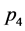 点代入到矩阵
点代入到矩阵 中,根据
中,根据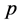 ,
, 的定义,特征根满足
的定义,特征根满足
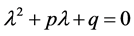
易得
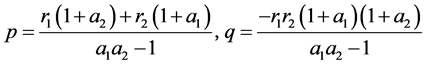
根据前面对 ,
,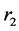 ,
,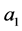 ,
, 的定义,得出
的定义,得出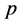 ,
,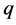 是异号的,即
是异号的,即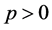 ,
, 或
或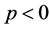 ,
,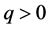 ,且
,且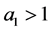 ,
, 。
。
当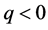 时,
时,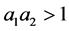 ,
,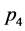 是鞍点。
是鞍点。
当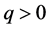 时,
时,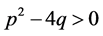 且
且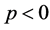 ,则
,则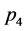 是稳定结点。
是稳定结点。
由于反馈调节时,存在负反馈调节等问题,在此不做详细的讨论。依据文献 [7] 中无自身阻滞问题的讨论,相当于对(8)式加了一个二次扰动,扰动后的系统的中心变成中心焦点或焦点等[4] 。
其次,筛选出的主要果蔬的年产量表和年消费量表1和表2所示。
5. 模型求解
为简便起见,以2010年果蔬的产量和消费量为初值,首先,第一步:利用MATLAB软件编程对2010年果蔬总的产量和消费量进行预测。
表1. 年产量
表2. 年消费量
根据2004~2010年的相关数据,由于年产量和消费量都集中在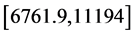 范围内,在不妨取最大容纳量分别为
范围内,在不妨取最大容纳量分别为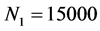 ,
, 。由于各自的固有增长率需要相关的实际调查统计、预测,为实现MATLAB的数值预测。不妨取
。由于各自的固有增长率需要相关的实际调查统计、预测,为实现MATLAB的数值预测。不妨取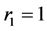 ,
,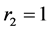 。
。
主程序如下
function xdot=equa(t,x)
r(1)=1;r(2)=1;N(1)=15000;N(2)=15000;a(1)=0.5;a(2)=0.5;
xdot=[r(1)*x(1)*(-1-x(1)/N(1)+a(1)*x(2)/N(2));r(2)*x(2)*(-1-x(2)/N(2)+a(2)*x(1)/N(1))];
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% the main function
% output two variables, which read the time t and x
clc
clear
t=2010:2:2020;
x=[11194,9685.1];
% the iteration solve
[T,X]=ode45('equa',t,x);
% display the solution on the window
[T,X]
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
当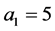 ,
, 时,
时,
ans =
1.0e+04 *
0.2010 1.1194 0.9685
0.2012 0.5848 0.1577
0.2014 0.0888 0.0232
0.2016 0.0122 0.0032
0.2018 0.0017 0.0004
0.2020 0.0002 0.0001
当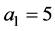 ,
,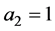 时
时
ans =
1.0e+04 *
0.2010 1.1194 0.9685
0.2012 1.3421 0.4516
0.2014 0.3794 0.1266
0.2016 0.0601 0.0200
0.2018 0.0083 0.0028
0.2020 0.0011 0.0004
第二步,分别将每种果蔬的年产量和年销量作为初值,代入到主程序中,同第一步的过程,这里省略数据。
6. 分析数据
MATLAB数据预测显示,由第一步可知:当参数取值不当,即当各因素反馈调控不当时,系统未来的产量和消费量随着时间的增大最终会趋于0,即无法维持人的正常生存,两种群都趋于灭亡。由第二步可知:水果中苹果和香蕉与蔬菜中马铃薯的消费量增加幅度大,因此要加大它们的种植面积。
依据定性分析和定量预测可知:较合理的年度消费量为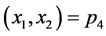 时影响果蔬的这三种主要因素对人体的正常物质需求有着一定程度的调控作用。各参数的取值对未来数据的预测有着重要的影响。由于各因素的干扰作用,对应于参数的取值需要一定的时间和实际实验逼近,现在不能给出较恰当的值或范围。
时影响果蔬的这三种主要因素对人体的正常物质需求有着一定程度的调控作用。各参数的取值对未来数据的预测有着重要的影响。由于各因素的干扰作用,对应于参数的取值需要一定的时间和实际实验逼近,现在不能给出较恰当的值或范围。
7. 给出建议
建议如下战略调整,调整果蔬的种植结构,增加营养价值高且价格相对便宜的果蔬的种植面积,尽可能达到 (当然受制于土地面积等因素影响)。
(当然受制于土地面积等因素影响)。