中部任意位置定向支承加固的压杆稳定性计算

Stability Calculation of Long Column under Directional Support in Any Position of Central

摘要: 为了丰富压杆的稳定性研究内容和方便工程应用之目的，用初参数法，对中部任意位置增加一个定向支承加固的七种压杆，建立了统一的变形方程和静力平衡方程。由各自的变形和静力约束条件，导出了求解临界压力的特征方程。借助软件，求得了压杆的长度因数与中部支承位置间的近似或精确关系；同时确定了中部支承的最佳位置和最小长度因数，以及最差位置和最大长度因数。经验证，结果符合理论预期。

Abstract: For enriching the research content about the stability of a long column and making it convenient in the engineering application, by using the initial parameters method, seven kinds of long column are strengthened by directional support in any position of central, and the unified deformation equa-tions and static force equilibrium equations are established. By the respective constraint conditions of deformation and static force, the characteristic equations of critical force are solved. By software, the approximate or accurate relationship between the factor of length of long column and the posi-tion of the central directional support are determined; at the same time, the best position of the central directional support and the minimum factor of length, and the worst position and the maximum factor of length are all determined. The result is verified according with theoretical expectation.

1. 引言

一些文献[1] -[6] 采用了统一的计算模型，得到了各种单跨压杆临界压力计算公式。工程实际中，为了增加压杆的稳定性，常在压杆中部适当位置增加某些支承。对这类压杆，材料力学教材[7] 等仅针对在压杆的中点采用固支加固的特殊情况，予以了简单有限的介绍，没有建立各种常见支承情况下，在压杆中部任意位置采取任意支承加固时，临界压力的统一求解方法，给工程应用带来诸多不便。文献[8] -[11] 等虽有研究，但鲜有给出简洁实用的解答，文献[12] [13] 等仅针对在压杆中部任意位置增加一个铰支加固的压杆的稳定性进行了计算。

为了丰富压杆的稳定性研究内容以及方便工程应用之目的，本文拟采用初参数法，研究在压杆中部任意位置增加一个定向支承(即该支承仅卡死压杆的转角，而毫不限制压杆的挠度)时，七种常见压杆的临界压力特征方程，并导出压杆的长度因数与该支承位置之间的定量关系，并进一步确定该支承的最佳位置和压杆的最小长度因数，以及最差位置和压杆的最大长度因数。

2. 公式推导

设长为l、中部任意位置x处定向支承加固的压杆的抗弯刚度为EI，当其处于微弯曲平衡状态，受力和变形情况如图1所示。

2.1. 变形关系

2.1.1. 变形方程

AB段即时，弯矩方程

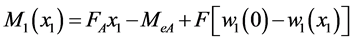
挠曲线近似微分方程

Figure 1. Micro bending equilibrium state of the whole

图1. 整体微弯曲平衡状态

转角方程

(2)

BC段即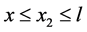时，弯矩方程

挠曲线近似微分方程

令，则的通解为

(3)

(4)

2.1.2. 变形边界条件

在(1)(2)中令x₁ = 0，得到压杆在A处的变形满足

(5)

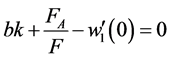(6)

压杆在B处挠度满足，由(1)(3)得

(7)

压杆在B处转角为零，即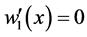,，由(2)(4)得

(8)

(9)

在(3)(4)中令x₂ = l，得到压杆在C处的变形满足

(10)

(11)

各种支承情况下的变形约束条件见表1。

2.2. 静力学关系

2.2.1. 静力平衡方程

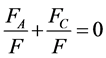(12)

2.2.2. 静力约束条件

根据压杆两端不同的支承情况，其静力约束条件见表1所述。

2.3. 特征方程

注意到表1中为零的项，则式(5)-(12)为关于 a、b、c、d和表1中的四个“？”共八个初参数的齐次线性方程组。由压杆处于临界状态时的变形和受力特征知，八个初参数即上述齐次线性方程组的解必非零，故令齐次线性方程组的系数行列式为零，即可导出求解压杆临界压力的特征方程。

2.3.1. 固支–定向–固支

结合表1，由(5)-(12)确定了一个关于初参数a、b、c、d、F_A/F、M_eA/F、F_C/F、M_eC/F的齐次线性方程组，其有非零解的充要条件是系数行列式为零，即求解压杆临界压力的特征方程为

2.3.2. 固支–定向–铰支

结合表1，由(5)-(12)确定了一个关于初参数a、b、c、d、F_A/F、M_eA/F、F_C/F、的齐次线性方程组，其有非零解的充要条件是系数行列式为零，即求解压杆临界压力的特征方程为

Table 1. Constraint conditions of deformation and static force

表1. 变形和静力约束条件

2.3.3. 固支–定向–定向

结合表1，由(5)-(12)确定了一个关于初参数a、b、c、d、F_A/F、M_eA/F、M_eC/F、的齐次线性方程组，其有非零解的充要条件是系数行列式为零，即求解压杆临界压力的特征方程为

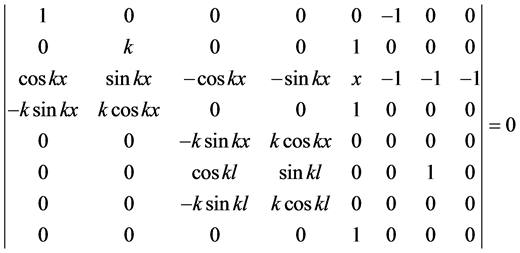
2.3.4. 固支–定向–自由

结合表1，由(5)-(12)确定了一个关于初参数a、b、c、d、F_A/F、M_eA/F、w₂(l) 、的齐次线性方程组，其有非零解的充要条件是系数行列式为零，即求解压杆临界压力的特征方程为

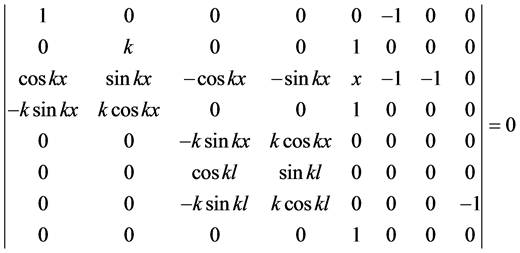
2.3.5. 铰支–定向–铰支

结合表1，由(5)-(12)确定了一个关于初参数a、b、c、d、F_A/F、F_C/F、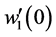、的齐次线性方程组，其有非零解的充要条件是系数行列式为零，即求解压杆临界压力的特征方程为

2.3.6. 铰支–定向–定向

结合表1，由(5)-(12)确定了一个关于初参数a、b、c、d、F_A/F、M_eC/F、、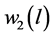的齐次线性方程组，其有非零解的充要条件是系数行列式为零，即求解压杆临界压力的特征方程为

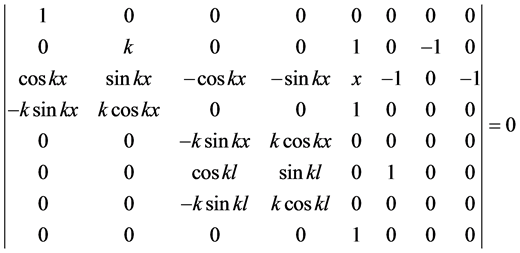
2.3.7. 铰支–定向–自由

结合表1，由(5)-(12)确定了一个关于初参数a、b、c、d、F_A/F、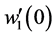、w₂(l)、的齐次线性方程组，其有非零解的充要条件是系数行列式为零，即求解压杆临界压力的特征方程为

3. 求解结果及验证

在2.3.1~2.3.7的特征方程中分别令x = ml，并用软件如maple等展开，得到关于m和u的特征

方程。

(1) 由软件分析知，2.3.1, 2.3.2, 2.3.5的特征方程为超越方程，只有近似解。借助软件绘制的曲线，则0 ≤ m ≤ 1且0.25 ≤ u ≤ 2区域曲线即为所求m-u曲线，见图2。在该图中，各m-u曲线的最低点坐标表示中部支承的最佳位置及最小长度因数；最高点坐标表示中部支承的最差位置及最大长度因数。近似关系见表2，粗体数字表示中部支承的最佳位置及压杆的最小长度因数，斜体数字表示中部支承的最差位置及压杆的最大长度因数。

(2)由软件分析知，2.3.3, 2.3.4, 2.3.6, 2.3.7的特征方程各有两个精确解，结果见表3，取二者中的极大值为u的解。图3中各m-u曲线的最低点坐标表示中部支承的最佳位置m₀及最小长度因数u_min；最高点坐标表示中部支承的最差位置m₁及最大长度因数u_max, 定量关系见表3。

当中部支承无限移近到压杆两端，即m = 0⁺或m = 1⁻时，得到等效的单跨压杆见表4，此时表2、表3中m = 0和m = 1时的长度因数与表4中等效单跨压杆的长度因数相等，结果符合理论预期。

4. 结束语

压杆的临界状态本质是微弯曲平衡状态，在推导上述特征方程时，把约束反力和相应的变形同时作为初参数，对整个压杆建立了统一的变形方程和静力平衡方程，符合压杆处于临界状态的真实情况。

Figure 2. The curve of m-u

图2. m-u曲线

Figure 3. The curve of m-u

图3. m-u曲线

Table 2. The factor of length(u)

表2. 长度因数(u)

Table 3. The analytical expressions

表3. 解析解答

Table 4. The equivalent long column

表4. 等效压杆

本文结果在丰富压杆的稳定性研究内容的同时，也为工程应用带来了方便。

基金项目

重庆科技学院本科生教育教学改革研究项目(CK2011B25)和研究生教育教学改革研究一般项目(YJG2014y008)。