1. 引言
规范中基桩的设计多以承载力为控制指标，但对超长桩而言，桩顶沉降量对结构的安全至关重要，工程中往往需要由桩顶沉降量来控制桩的竖向承载力。本文在荷载传递解析法的基础上，针对桩周土体成层的特点，由实际工程经验推导了超长单桩的竖向侧阻荷载传递模型，并由此建立了桩顶沉降量与竖向承载力之间的关系，提出按桩顶沉降量控制基桩竖向承载力的分析方法。
2. 大直径超长基桩荷载传递机理
2.1. 大直径超长基桩桩侧阻力传递机理
国内外众多研究者对超长桩侧阻力的研究，一般采用荷载传递法，因此提出了多种荷载传递函数。目前，工程上采用比较多的是双折线模型、三折线模型和假设由数个函数组合的传递函数：
(1)
式中，f(s)为桩侧(或桩端)摩阻力；s为桩身位移或桩端沉降；
及
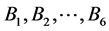为参数。
由于上式各项中的参数很难确定，故实际分析中仅选用某一项作为荷载传递函数来分析实际工程中单桩受力情况。
在众多学者的研究中，阳吉宝 [1] 在多次研究后，考虑土的连续性，将式(1)中第一项，即双曲线函数修正后作为传递函数
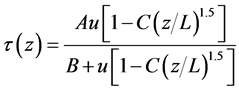(2)
式中，A, B——岩土参数；C——综合参数，按表1取值，可以分层；L——桩长。
由式(1)传递函数表达式的第一项
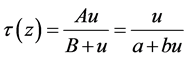(3)
对该式分析，不难发现，当剪切位移u无限大时，桩侧摩阻力接近一常数。
(4)
可见A的物理意义是描述桩侧极限摩阻力的一个常数。当剪切位移趋于0时
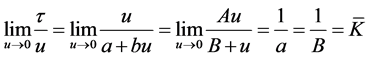(5)
趋近于过原点所做的
曲线的斜率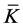
，B的物理意义为
的倒数。
对式(2)进行转化可得
(6)
可以看出，式(6)是在式(3)的基础上，对系数B除以一个小于1的系数，也即对B进行了放大。而我们在实际工程中，根据工程经验，获得了下式
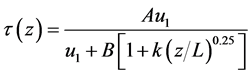(7)
式中，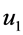
的单位取为mm；
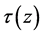的单位取为kPa；k是岩土体综合参数，分层取值，见表2。
2.2. 实例
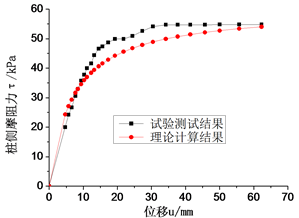
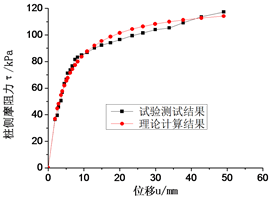
南京水利科学研究院在400 gt土工离心机上对某大桥桩基进行了模型试验。根据工程地质勘测报告[2] ，可以确定出每层土的A和B值分别取15和0.6，d取为0.5。计算结果和试验测试结果对比如图1。
从图1可以看出，本文总结的超长单桩桩侧传递函数能较好地反映桩顶荷载沿桩体的传递规律。
3. 由桩顶沉降控制超长单桩竖向承载力
取桩端荷载传递函数如下[3]
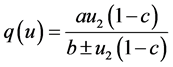(8)
式中，a，b为岩土参数；c为综合参数，意义同桩侧阻。
由上文的桩侧和桩端荷载传递函数，借用数学手段，计算桩顶沉降处于不同水平所对应的桩顶荷载值，实现以桩顶沉降量来控制基桩承载力的设想。
在分析桩顶沉降控制值
所对应的桩顶荷载值P时，首先需确定桩身处于承载极限状态下的桩顶荷载Pmax及对应的桩顶沉降量umax这两个重要的判别参数，其计算步骤如下：
表1. C值取值范围
表2. k值取值范围
(a) (b) 
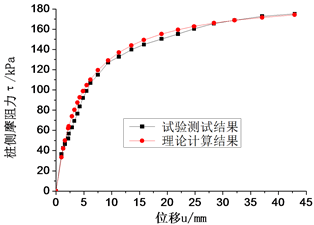
(c),(d)
Figure 1. The relationship contrast figure of pile side friction and the relative displacement between of piles and soil by test and calculation; (a) pile 1; (b) pile 2; (c) pile 3; (d) pile 4
图1. 试验与计算的桩侧摩阻力与桩土相对位移的关系对比图；(a) 桩1；(b) 桩2；(c) 桩3；(d) 桩4
(1) 按不同土层划分桩身单元，共n层，计n + 1个截面；
(2) 当桩身处于承载极限状态时，各土层侧阻及端阻均得到充分发挥，侧阻实际变形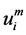
均应不小于变形临界值
，桩端土的变形应不小于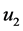
。桩身各截面的轴力和变形计算如式(8)。根据Bowles [4] 的研究，发挥最大侧阻所需土层滑动量的数量级大约为5~10 mm，计算时根据岩土的实际情况取值；
(3) 式(8)还可用于计算当桩身处于非极限状态时桩身的荷载分布和沉降。此时，各土层侧阻及端阻尚未充分发挥，侧阻实际变形及桩端土的变形可取较小值0~5 mm。
；
；
；
；
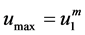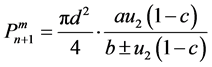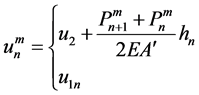，取较大值；
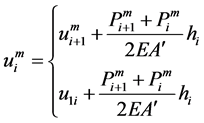，取较大值。
式中，d——桩径(m)；
——桩身i截面上的轴力值，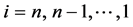
，下同(kN)；
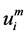——桩身i截面的竖向变形量(mm)；E——桩身弹性模量(1 × 106 Pa)；
——桩身截面积(m2)；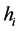
——桩身第i层土体厚度(m)。
若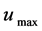
不大于预期沉降控制值
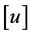，则桩顶承载力
，可结束计算；否则，调整综合参数
、
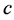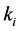和各土层变形临界值
至计算结果满足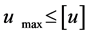
。如若计算非极限状态时桩身荷载和沉降的关系，
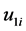系各土层的竖向变形量。
为便于工程应用，现以上述分析原理和方法，采用FORTRAN语言，编制了相应的计算程序，计算的程序框图如图2所示。
具体计算时，应根据现场试桩结果确定岩土参数A、B及k值，并计算相同岩土环境下的其它超长单桩沉降及桩顶承载力。
4. 计算实例
本节以苏通大桥北岸N-1静载荷试桩试验资料为例，对本课题推导的以沉降控制荷载的方法及开发的程序进行校验。
现场勘查资料显示，桥位区所处地层主要为粉砂、粉砂与亚粘土互层、粉砂、亚粘土、砾砂。
试桩直径1.0 m，桩长76 m，桩顶标高+2.2 m，桩底标高−73.8.0 m。静载试验采用锚桩法，加载为
慢速维持荷载法，最大加载量为11,000 kN，共分10级，每级1000 kN。试验的设计、成桩工艺和加卸载方法均严格按照相关规范进行操作。
实测资料提供的相应数据及各土层岩土参数如表3。
表中，
，
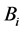是根据原始报告数据计算而来，
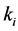根据岩土层情况取经验值。a，b及c是桩端土层的参数，由底层的
、
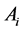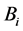和c计算而来，此处
，
，
。本算例的预期沉降控制值
，计算的结果见图3和图4 (公式中有“+”和“−”，本文的计算结果均取“−”时的大值)。桩顶不同外载作用下的位移则是调整每层的层位移
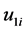计算而来。
由图3可以看出，在桩顶作用10,000 kN时，本文公式的计算结果可以很好的拟合试验测试结果，但数值计算的沿桩身的轴力则要大于实际测试结果。
图4中，在相同桩顶荷载的作用下，本文公式计算的桩顶沉降普遍要大于实际测试的结果，即本文公式由沉降控制桩顶荷载时，计算出的荷载普遍要小于测试结果，结果偏于保守。而数值计算的位移要大于测试和本文公式计算的。
桩顶总沉降量大于或等于40 mm时，达到破坏标准值，根据本文公式计算可得此时的桩顶荷载为11,358 kN，即由沉降控制计算而来的桩极限承载力为10,000~11,000 kN，和实际测试结果相符。
表3. 实测土层数据
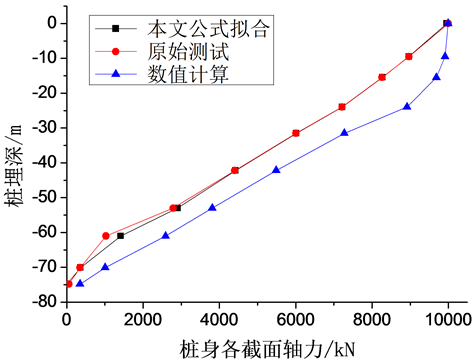
Figure 3. The axial force distribution along the pile shaft when the pile load is 10,000 kN
图3. 桩加载10,000 kN时沿桩身轴力分布图
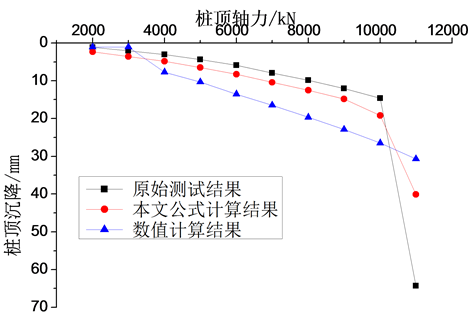
Figure 4. The load-displacement (Q-S) curve
图4. 桩的荷载–位移(Q-S)曲线
5. 小结
本文在荷载传递解析法的基础上由工程实践提出了一种新的基桩桩侧摩阻力传递模型，并推导了全桩荷载分布函数，编写了由沉降控制桩顶荷载的程序，适用于不考虑深度效应的灌注桩。
计算实例表明该方程可以很好地模拟基桩的桩身荷载分布，并能由桩顶沉降控制值计算出桩的极限承载力，对超长单桩的设计具有优化作用。