1. 序言
机械设备的摩擦过程异常复杂,再加上环境和界面介质的作用,使得在表面摩擦过程中产生形貌不同的磨粒 [1] 。磨粒往往携带有不量关于摩擦的信息,其颜色、尺寸和形貌等信息又和磨损方式密切相关 [2] 。表1给出了各种摩擦颗粒分类以及每种颗粒的大致特征的表格 [3] 。
从表1中可以看出,这五种磨粒中正常的滑动磨粒和切削磨粒比较容易区分,因为正常的滑动磨粒的尺寸在五种磨粒中最小,一般可以通过尺寸的大小来判断。而另外四种磨粒尺寸大小均匀重叠的部分,故不好用尺寸来区分。对于切削磨粒和其他三种磨粒(疲劳剥落、层状磨粒、严重滑动)最大的区别在于其边界形状一般呈细长、卷曲状。可以通过计算磨粒长轴和短轴之比,来和其他的磨粒进行区分。对于剩下的三种磨粒,尺寸均有重叠部分,边界形状也相似,故用上述的方法不能有效的进行区分。
2. 铁谱磨粒图像轮廓K值计算法
2.1. K值计算法原理
根据观测对空间或者时间的随机变量的统计性质进行调查时,往往可以得到与波数变动相对应的频谱。这些变动是否为分形可以通过频谱的研究就能阐明。从频谱的观点来看,所谓改变观察尺度就是改变截止频率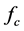 。这里的截止频率是指把较此更细小的振动成分舍去的界限频率。因此,如果某变动是分形的,那么即使改变截止频率也不会改变频谱的形状 [4] 。
。这里的截止频率是指把较此更细小的振动成分舍去的界限频率。因此,如果某变动是分形的,那么即使改变截止频率也不会改变频谱的形状 [4] 。

Table 1. Classification and preliminary characteristic of various kinds of wear particles
表1. 各种磨损颗粒的分类和初步特征
图像中选取不同的截止频率,得到的图像的灰度值的差异也不同。而K值法就是改变图像中的截止频率,从而得到图像中不同的灰度差值,将这些截止频率为横坐标,图像中灰度的差值之和取对数为纵坐标。然后对图上的折线段进行线性拟合,拟合的斜率就是K [5] 。
具有分形特征的图形,在某一个尺度范围内满足 。判断图形是否为分形只需判断图像是否存在无标度区间。一般判断有无标度区间的方法有三种[6] :
。判断图形是否为分形只需判断图像是否存在无标度区间。一般判断有无标度区间的方法有三种[6] :
1) 观察法:在双对数坐标中绘出 与
与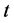 的关系,通过观察找到线性关系较好的区间作为无标度区间,若没有线性较好的区间,那么该图形不具备分形特性。这种方法总体而言是正确的,且方便有效。但存在一定的主观因素。
的关系,通过观察找到线性关系较好的区间作为无标度区间,若没有线性较好的区间,那么该图形不具备分形特性。这种方法总体而言是正确的,且方便有效。但存在一定的主观因素。
2) 分段直线回归法:假设测量点分布在3条线段构成的折线附近。通过分段线性回归,以总的回归线差平方和最小作为目标,求出中间一段斜率。这种方法只能保证测量点在无标度区间内按一定斜率分布。
3) 逐渐逼近法:选定一个起始点,逐点进行直线的线性拟合并求出线性拟合系数,以拟合系数最好的作为直线的斜率,该长度区域即为无标度区。若拟合不满意,可调整截取长度重新进行拟合。
2.2. 基于逐渐逼近法的K值计算
本文通过逐渐逼近法对图像进行线性拟合得出截止频率在3.0~4.0区间线性中直线的线性拟合效果最好。所以图形符合分形特性,其无标度区间为3.0~4.0。
K值计算法的步骤:首先将铁谱磨粒图像灰度化处理,然后在图像表面随机选取64 × 64像素的正方形区域,对区域中的灰度值进行逐个比较,将相邻的两个灰度值之差相加,设区域中所有相加值和为S。选择不同的截止频率,从而得到不同的S值,从而形成以截止频率为横轴,lgS值为纵轴的折线图,然后对图上的折线段进行线性拟合,并求出线性拟合后直线的斜率,设其斜率值为K。图1(a)为严重滑动磨粒64 × 64像素的正方形区域,当严重滑动磨粒进一步放大成一个个具有一定像素值的小方格,如图1(b)所示,图中方格中的数字表示该方格的灰度值。
根据上述过程,K值计算法的步骤分为三步:
图像获取;本试验图像的获取选用分析式铁谱仪,放大倍数为500倍;
灰度处理;分析式铁谱仪所获取的图像是彩色的,将图像灰度化处理,为后续的步骤做准备;
阈值分割;采用阈值分割法将图像的背景色变成黑色,方便K值的计算;
选取目标区域;随机选取64 × 64像素区域,在计算机图像中,白色的灰度值为255,黑色的灰度值为0,不同的灰度对应不同的灰度值;
计算不同S值;S值是指在64 × 64像素区域中所有灰度值的和值。改变不同的截止频率,得到不同的S值;
生成InS-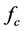 图像并进行线性拟合;线性拟合的斜率就是所求的K值。
图像并进行线性拟合;线性拟合的斜率就是所求的K值。

 (a) (b)
(a) (b)
Figure 1. Severe sliding grinding grains enlarge figure
图1. 严重滑动磨粒放大图
3. 三种铁谱磨粒图像的K值计算
对70种层状磨损颗粒、疲劳磨粒及严重滑动磨粒样本进行K值进行计算。首先选取截止频率在3.0~4.0的区域,然后计算图像的S值,最后对图像进行线性拟合。图2、图3及图4分别表示层状磨粒、疲劳磨粒及严重滑动磨粒在不同截止频率下,其和值S变化,图中的斜率就是所求的K值。
对70个样本的层状磨粒进行K值统计,层状颗粒的K值在0.110~0.350之间,疲劳后期颗粒的K值在0.375~1.30之间,严重滑动磨粒的K值在1.160~1.955之间。
4. 结果分析
以磨粒的分形维数值为纵坐标,K值为横坐标作二维坐标图,如图5所示。
通过对严重滑动磨粒、层状磨粒、疲劳(后期)磨粒的分形维数和K值形成的坐标图可知:
1) 根据纵坐标(分形维数)可以看出疲劳(后期)磨粒和层状磨粒、严重滑动磨粒和层状磨粒分布均有不同程度的重叠,所以不能很好的区分这三种磨粒。
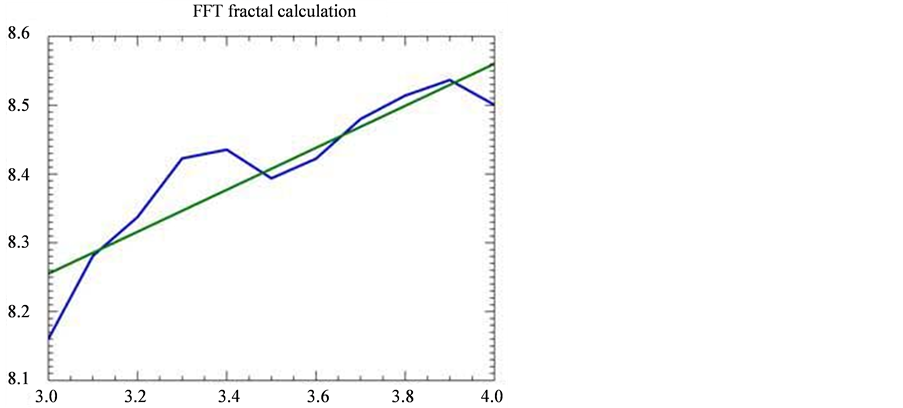
Figure 2. The K value calculation of layer wear particles
图2. 层状磨粒的K值计算
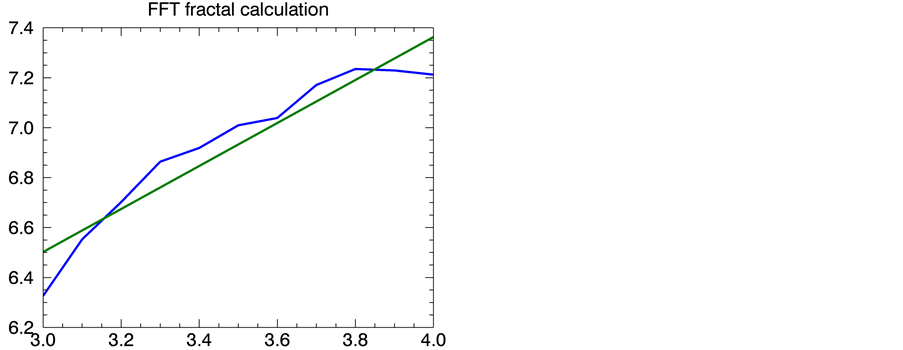
Figure 3. The K value calculation of fatigue wear particles
图3. 疲劳磨损颗粒K值计算
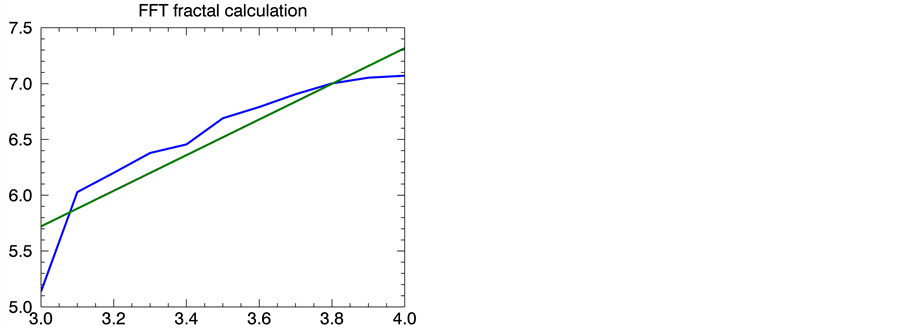
Figure 4. The K value calculation of severe sliding wear particles
图4. 严重滑动K值计算

Figure 5. K value-fractal dimension coordinate
图5. K值–分形维数坐标图
2) 根据横坐标(K值)可以看出严重滑动磨粒、层状磨粒和疲劳(后期)磨粒的分布基本没有重叠,所以可以用来对着三种磨粒进行区分。
3) K值从物理意义上表示磨粒图像表面灰度值的不同差异度。严重滑动磨粒的K值最大,表明其表面明暗程度差距明显。层状磨粒K值最小,说明其表面色差比较小。K值计算法为铁谱磨粒识别提供了一种新方法,具有一定的理论意义和实用价值。
5. 结论
通过计算严重滑动磨粒、层状磨粒和疲劳(后期)磨粒的K值表明,疲劳(后期)磨粒和层状磨粒、严重滑动磨粒和层状磨粒的分形维数有不同程度的重叠,不能很好的区分磨粒的种类。而三种磨粒的K值分布基本没有重叠,故对磨粒分类有良好的效果。