1. 引言
重力勘探观测和研究的是天然重力场，是以研究对象与围岩存在的密度差异为前提条件。观测与研究天然重力场的变化规律，从观测重力值中去掉与研究对象无关的各种因素的影响，用于探究地质一种物探方法[1] -[4] 。其主要用于研究深部和区域等大范围的地质构造，从而探查油气远景区。且随着仪器精度的提高和计算机处理方法的改进，在高精度测量方面的应用取得了很大的进展[5] -[10] 。采用经各项改正后的重力异常，研究地壳内部的结构，探查固体矿产和油气资源的分布，是重力勘探的重要研究内容。而实现这些研究的基础则是建立地质模型，进而研究各种地质模型的正演问题和反演问题，给出对应的正反演理论和方法。这些方法现今已成为重力勘探的主要研究内容[10] -[14] 。
在二维重力正演模拟发展的几十年中有效地解决了不少地质构造问题，但是在一条测线的剖面下只能探测到地质体剖面的形态，并不能反映出地质体全面的形态，造成重力反演多解性与难解性的问题[15] [16] 。刘光夏等(1998)在河北省中部地区采用剥层方法做了重力正演，获得较好的地壳结构分布[10] [12] 。吴燕冈等(2005)在中国境内沿北纬40˚截取了一段长剖面，对布格重力异常进行了正演拟合计算。所谓的正演问题就是给定地下某种地质体的形状、产状和剩余密度等，通过理论计算来求得它在地面上产生的异常大小、特征和变化规律[7] 。柯小平等(2009)对青藏高原东部下察隅地区做了重力正演模拟[11] 。杜劲松等(2012)对球冠体积分的重力异常正演方法作了简要分析[6] [17] 。
目前我国的大范围重力勘探已经完成，局部精细的地质区块并没有实现重力勘探。现在那些难开发的多构造的复杂工区，重力勘探就出现多解释，难解释的现象。主要是因为重力勘探在z轴数据的缺失，还有2D重力勘探只能反应地质体切片信息，不能反应地质块体全面的信息。3D重力勘探的研究就显得极其重要，本文就着重分析3D重力勘探的正演问题。通过模拟地下地质体，在MATLAB软件中实现出三维地质体的重力信息，包括布格重力异常，重力异常各阶导数的信息[18] -[20] 。本本的研究是基于MATLAB软件进行开展的。
2. 方法原理
计算某个地质体所产生的重力异常，是根据万有引力来进行计算。通常先计算地质体的剩余质量所产生的引力位，然后在求出引力位沿重力方向的导数，其方法如下：
以地面上某一点O作为坐标原点，z轴铅垂向下，即沿重力方向，x、y轴在水平面内，见图1。
若地质体与围岩的密度差为
，地质体内某一体积元
，其坐标为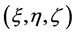
，它的剩余密度为
，则
。令计算点A的坐标为
,剩余质量元到A点的距离为
，
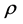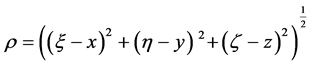(1-1)
则地质体的剩余密度在A点处对单位质量所产生的引力位为
(1-2)
其中：v为地质体的体积，G为万有引力常数。因为选择z的方向就是重力的方向，所以重力异常就是剩余质量的引力位沿z方向的导数，即
(1-3)
如果地质体的形状和埋深沿水平方向均无变化，且沿该方向延伸无限，此时的地质体称为二度地质体。将上式中的y轴方向选作为二度地质体的延伸方向，
的积分限由
到
，令y = 0，就可得到在沿x方向剖面上计算二度体重力异常的基本公式，当剩余密度是均匀的时，则可提到积分符号外，即
(1-4)
式中S为二度体的横截面积。
我们还可以推导出计算：
重力异常垂向梯度异常的基本公式为：
(1-5)
Figure 1. Calculate the geological abnormal weight force diagram
图1. 计算地质体重力异常示意图
重力异常水平方向沿x的梯度异常的基本公式为：
(1-6)
重力异常沿水平y轴方向的梯度异常的基本公式为：
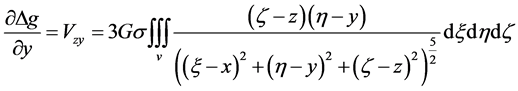(1-7)
重力异常垂向二阶导数的基本公式为：
(1-8)
重力高阶导数可以突出浅而小的地质体的异常特征压制区域性深部地质因素的影响，在一定程度上可以划分为不同深度和大小的异常源产生的叠加异常，且导数的次数越高，这种分辨能力就越强。这些功能主要是因为导数阶次越高，则异常随中心埋深加大而衰减越快，从水平方向来看，基于同样的道理，阶次越高的异常范围越小，因而无论从垂向看或者从水平方向看，高阶导数异常的分辨能力提高了[21] -[23] 。
3. 2D地质模型重力正演模拟
为了简化规则几何形体正问题的解法，假设地质形体孤立存在，密度均匀，地面水平，所取剖面为中心剖面。由于不同的地质因素往往会在重力异常平面等值线图上或剖面图上产生相似的异常特征，因此根据某一局部异常来判断它是由什么地质因素引起的，常常不是一件容易的事，为此，本文一一利用理论推导出各种地质体的
、
、
、
、
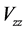的计算公式[24] -[27] 。并且作出了相应的异常剖面图与等值线图[28] -[30] 。
二维重力正演模拟是对模拟地质体切片进行二维数据分析，在XOZ的平面内进行成图分析地质体的相关数据。本文选取比较典型的密度均匀的球体模型进行分析，在实际工作中，一些近于等轴状的地质体，如矿巢、矿囊、岩株、穹窿构造等，都可以近似当作球体来计算它们的重力异常，特别当地质体的水平尺寸小于它的埋藏深度时，效果更好。为了简便，总是把地面当做水平面，即是XOY坐标面，z轴铅垂向下，代表重力方向。
对于均匀球体来说，它与将其全部剩余质量集中在球心处的点质量所产生的异常完全相同。设球心的埋藏深度为D，球的半径为R，剩余密度为σ，则它的剩余质量为：
(2-1)
将坐标原点O选为球心在地面的投影处，因球的对称性，我们只需要研究通过O点的任意水平剖面上异常的分布即可，设该剖面于x轴重合，则在剖面上任一点P(x, 0)处的重力异常，从基本公式可知，令
，
，
，便可获得其表达式为
(2-2)
本文所建的球体模型的参数为：D = 100 m，R = 50 m，σ = 1 g×cm−3。分别对所建的球体模型进行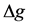
、
、
、
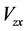分析。
(一) 分析上式(2-2)，可以获得如图2沿该中心剖面上异常分布的基本特征是：
1) 在x = 0处，异常取得极大值。因含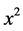
项，故异常是相对原点为对称分布的。当
时，异常趋近于零，其形态就图2所示。
2) 当异常为极大值的
时，对应的该点之横坐标以
表示，则由关系式
可解得
(2-3)
例如，取n = 2，得
说明异常半极值点的横坐标为球心埋深的0.766倍，利用它解反问题时求D十分方便。
3) 当D不变，使M加大m倍时，异常也同样加大m倍；而当M不变，D增大m倍时，异常极大值减为原来的
，而
值将增大为原值的m倍。所以，随着D的加大，异常迅速衰减。曲线明显变缓。
(二) 重力异常水平方向沿x的梯度异常的基本公式为：
(2-4)
分析上式，可以获得如图3沿该中心剖面上异常分布的基本特征是：
值在0点处，其值为0。在其左侧，其值最大，在其右侧，其值最小。图形成中心对称分布。当
时，
值为0。
(三) 重力异常垂向梯度异常的基本公式为
(2-5)
分析上式，可以获得如图4沿该中心剖面上异常分布的基本特征是：
值与
值一样，同样是在
Figure 2. The sphere of two-dimensional Bouguer anomaly section
图2. 球体二维布格异常剖面图
Figure 3. 2D derivative of gravity anomaly x direction of sphere
图3. 球体二维重力异常x方向的导数图
Figure 4. 2D derivative of gravity anomaly z direction of sphere
图4. 球体二维异常z方向上的导数图
原点处取得最大值，不同之处是：当
时，
值是从负值逐渐趋于0的。
(四) 重力异常垂向二阶导数的基本公式为
(2-6)
分析上式，可以获得如图5沿该中心剖面上异常分布的基本特征是：重力异常垂向二阶导数值的图形与
和
是一样的。都是当
时，值是逐渐趋于0的。不同的是其值大小不一样，且
值的负值小于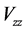
的负值，
值比
值更加精确。
4. 3D地质模型重力正演模拟
对于均匀球体来说，它与将其全部剩余质量集中在球心处的点质量所产生的异常完全相同。设球心的埋藏深度为D，球的半径为R，剩余密度为σ,则它的剩余质量为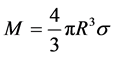
。将坐标原点O选为球心在地面的投影处，因球的对称性，我们只需要研究通过O点的任意水平剖面上异常的分布即可，设该剖面于X-Y平面重合，
则在剖面上任一点P(x, y)处的重力异常的表达式为
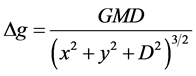(3-1)
图6为在MATLAB中所建的地质球体模型。图中所示球体的参数为：D = 100 m，R = 50 m，s = 1 g×cm−3。地质区域的参数(见图6)。
三维球体布格重力异常基本公式：
(3-2)
获得如图7沿该中心剖面上异常分布的基本特征是：
三维球体的布格重力异常数值在(0, 0)处，异常取得极大值为0.035 g·u。因有
和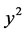
项，故异常是相对原点为对称分布的；当x与y同时趋近于
时重力异常趋近于零，其形态见图7。在平面图上等值线为以球心在地面的投影点为圆心的许多不等间距的同心圆；
三维球体重力异常x方向水平梯度基本公式为
(3-3)
Figure 5. 2D vertical second derivative of a sphere
图5. 球体二维垂向二阶导数图
Figure 6. Three-dimensional sphere geological model
图6. 三维球体地质模型
获得如图8沿该中心剖面上异常分布的基本特征是：
三维球体重力异常x方向水平梯度值在(−50, 0)附近处最大，在(50, 0)附近处最小，从而确定了地质球体的水平边界。在x轴左侧区域梯度值全为正值，在右侧区域梯度值全为负值，且两侧的图形相同，其形状见图8。在平面上等值线为以(0, 0)点沿x轴对称分布的两个不等间距的类同心圆；
三维球体重力异常y方向水平梯度基本公式为
(3-4)
获得如图9沿该中心剖面上异常分布的基本特征是：
三维球体重力异常y方向水平梯度值在(0, −50)附近处最大，在(0, 50)附近最小，从而确定了地质体球体在y方向上的边界。在y轴下侧区域梯度值全为正值，在上侧区域梯度值全为负值，且两侧的图形的相同，其形状见图。在平面上等值线为以(0, 0)点沿y轴对称分布的两个不等间距的类同心圆；
(a) (b)
Figure 7. Three-dimensional sphere geological model. (a) The Bouguer gravity anomaly in section; (b) The Bouguer gravity anomaly contour
图7. 球体三维布格重力异常的剖面图与等值线。(a) 布格重力异常的剖面图；(b) 布格重力异常的等值线
(a) (b)
Figure 8. Sphere three-dimensional profile and contour map of x direction. (a) x direction of the gravity anomaly gradient profile; (b) Gravity anomaly contour of x direction gradient
图8. 球体三维重力异常x方向梯度的剖面图与等值线图。(a) 重力异常x方向梯度的剖面图；(b) 重力异常x方向梯度的等值线
三维球体重力异常z方向梯度基本公式为
(3-5)
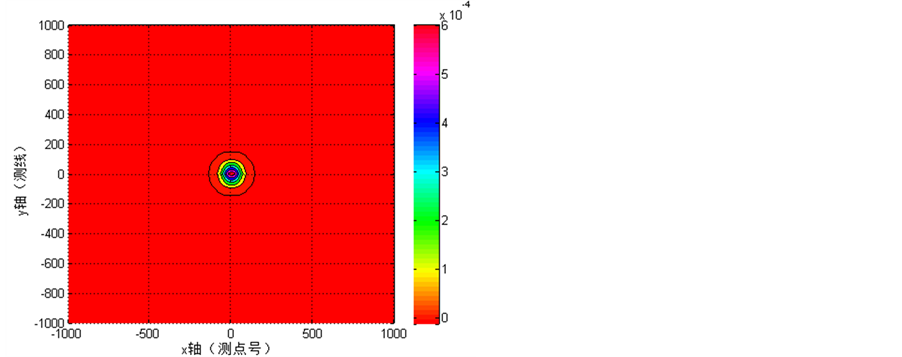
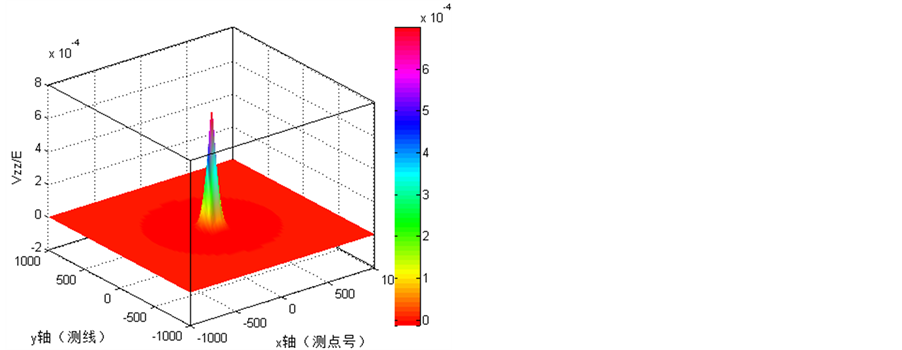
分析图10得到：
三维球体重力异常z方向水平梯度值在(0, 0)处，异常取得极大值。异常是相对原点为对称分布的，当x与y同时趋近于
时重力异常趋近于零，其形态见图。在平面图上等值线为以球心在地面的投影点为圆心的许多不等间距的同心圆；
三维球体重力异常垂向二阶梯度基本公式为
(a) (b)
Figure 9. Sphere three-dimensional profile and contour map of y direction. (a) y direction of the gravity anomaly gradient profile; (b) Gravity anomaly contour of y direction gradient
图9. 球体三维重力异常y方向水平梯度的剖面图与等值线图。(a) 重力异常y方向梯度的剖面图；(b) 重力异常y方向梯度的等值线
(a) (b)
Figure 10. Sphere three-dimensional profile and contour map of z direction. (a) The vertical gradient of gravity anomaly z direction in section; (b) The z direction vertical gradient of gravity anomaly contour
图10. 球体三维重力异常z方向垂向梯度的剖面图与等值线图。(a) 重力异常z方向垂向梯度的剖面图；(b) 重力异常z方向垂向梯度的等值线
(a) (b)
Figure 11. Three-dimensional sphere gravity anomaly vertical second derivative profile and contour map. (a) The z direction vertical gravity anomaly second order gradient profile; (b) The z direction vertical gravity anomaly second order gradient contour map
图11. 球体三维重力异常垂向二阶导的剖面图与等值线图。(a) 重力异常z方向垂向二阶梯度的剖面图；(b) 重力异常z方向垂向二阶梯度的等值线
(3-6)
获得如图11沿该中心剖面上异常分布的基本特征是：
三维球体重力异常垂向二阶梯度值在(0, 0)处，异常取得极大值为
。异常是相对原点为对称分布的，当x与y同时趋近于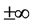
时重力异常趋近于零，但是其值会在x轴下侧趋于零形态见图。在平面图上等值线为以球心在地面的投影点为圆心的许多不等间距的同心圆。
5. 结论与认识
本文是基于MATLAB环境下建立球体模型。并且深入总结了二维重力正演模拟的方法与原理，还进一步推导出部分三维重力异常与各阶导数的公式，分析总结了三维重力正演模拟的成果图。在MATLAB环境下，编写程序，编入模型地质体的参数，输入重力布格异常公式与各阶导数异常的剖面图与等值线图。总结来说，本文的研究内容与成果主要包括以下几个方面：
1) 二维重力正演模拟的方法与原理包括对简单规则形体的深入总结。其中密度均匀的球体的认识为在原点处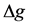
、
、
值都为最大，
值为0。
与
相比，
算法更能突出局部小地质体，反应出垂向高阶导数突出局部异常体与区分叠加异常体的极大利用价值。三维重力正演方法是对三种地质模型，其中对密度均匀的球体的结论为：重力异常等值线图、
、
的等值线图都为圈闭呈圆形，异常值中心部分高，四周低，有极大值。其剖面的分析结果与二维曲线图的分析结果是一样的，不同的是y轴信息存在，对解反问题时大有帮助；
2) 经过对二维重力正演方法与原理的深入总结和三维重力正演的推演计算成图分析，总结了部分关于重力正演的知识。得出二维重力正演只能成曲线图，y轴信息缺失。三维重力正演形成曲面图，测线覆盖整个工区，信息较为全面。对之后重力反演会有很大的帮助。而且对于局部较小的地质体，如小断层、小幅度构造、小砂体等在三维重力勘探采集中就不会被漏掉。此外通过对模拟地质体的重力异常高阶导数分析得出，小的局部地质体可以通过高阶导数分析得出其规模形状。从典型模型的二维重力正演与三维重力正演对比分析过程中还可得出三维重力正演可以确定地质体的边界，而二维重力正演只能确定地质体在测线方向上的边界。