1. 引言
由上、下两个平台和六个可伸缩的支腿通过运动副连接而成的具有六自由度运动能力且能够模拟空间各种位姿运动的Stewart并联机构最初被设计用作飞行员的飞行模拟器[1] 。由于这种机构与传统的串联机构相比具有精度高、刚度大、结构稳定、承载能力强、运动惯量小、动态特性好、反解易获得等优点，其逐渐在航空航天、天文观测、汽车工业、隔振平台、高档数控机床以及起重运载等领域中得到广泛的应用 [2] [3] 。
由于在具体应用中涉及机械、电机(或液压)驱动、控制、传感等多学科再加上其运动学正解的多解性，使得Stewart并联机构在仿真建模和实际应用中并不容易。特别是在对Stewart平台结构设计和控制器设计时，需要对平台相关的运动学、动力学参数进行计算，以此来为结构设计提供理论依据。而在运动学、动力学参数计算过程中存在大量的数值计算和矩阵计算，形式繁琐且容易出错，不利于工程实际应用 [4] [5] 。为了解决这个问题，本文采用ADAMS建立Stewart并联机构的模型，基于MATLAB建立模糊PID控制器模型，通过联合仿真对Stewart并联机器人的控制参数进行整定，对其性能进行仿真设计，此种方法由于基于商用软件，因此具有简单、不涉及复杂的理论和公式的优点 [6] - [9] 。
2. Stewart并联机构
Stewart并联机构如图1所示，其由动平台、静平台、球铰和六个伸缩缸构成，伸缩缸可以是液压缸也可以是电动伸缩缸，其下端通过球铰和静平台相连，上端通过球铰和动平台相连。
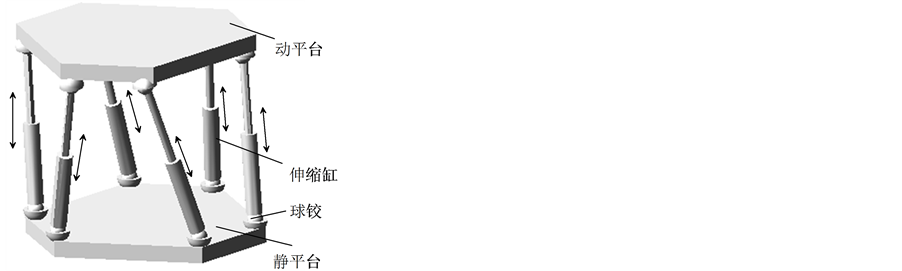
Figure 1. Schematic diagram of stewart parallel robot
图1. Stewart并联机构原理简图
将Stewart并联机构作为机器人操作的机器系统即为Stewart并联机器人。由于伸缩缸两端为球铰，对伸缩缸的输出杆长度进行控制即可控制动平台的姿态，而伸缩缸是由电机或液压带动的，由于电机或液压的伺服驱动技术较成熟且响应时间远小于机器人的响应时间 [10] ，因此本文建模时将电机或液压等效于比例环节，仅对Stewart并联机器人的控制性能分析。
3. Stewart并联机器人控制模型
3.1. Stewart并联机构的动力学模型
在工作过程中，平台的受力都集中在动平台上，忽略伸缩缸的质量后，系统的动能可以表示为
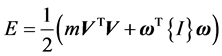(1)
式中，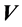
，
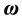分别是动平台的速度矢量和角速度矢量，因此其取值为
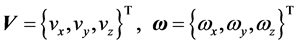(2)
，
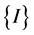分别是动平台的质量和惯性张量，惯性张量取值为 [11]
(3)
动平台的动能还可以表示成以下形式
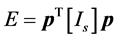(4)
式中，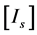
为广义惯性张量，它是机构本身的力学量，其取值为
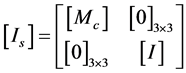(5)
式中，
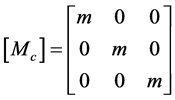(6)
为动平台的广义输出速度，其表示为
(7)
动平台的广义惯性力可以表示为
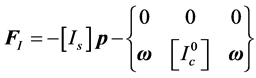(8)
式中，
为动平台的角速度反对称矩阵，它可以表示为
(9)
设动平台不受外力则所受总力等于广义惯性力，即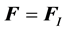
。
由能量守恒可得伸缩缸满足方程
(10)
式中，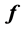
、
分别为6个伸缩缸的驱动力和速度。
由于伸缩缸的速度满足
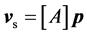(11)
则代入式(10)可得
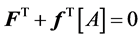(12)
因此伸缩缸受力满足
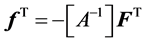(13)
式中，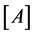
为并联平台的一阶影响系数，当已知并联平台上平台的运动状态和受力状态时，就可以求出6个伸缩缸的受力情况。
3.2. 基于ADAMS的Stewart机构模型
设动平台直径为200 mm，静平台直径为400 mm，伸缩缸由伸缩杆和缸体构成，伸缩杆长度2 m，直径50 mm，缸体长度1.5 mm，内径50 mm，外径80 mm，杆件材料为Q
235A
，在ADAMS中直接构建Stewart平台的机械结构模型如图2所示。并按如下设置Stewart并联机构的约束和运动副：输出杆和缸体间为移动副，伸缩杆和动平台间为球铰连接，缸体和静平台间为球铰连接，静平台为固定架。
3.3. 模糊PID控制
由于并联机器人存在着非线性、时变性等不确定性因素，传统PID控制效果将难以达到预期的目标，采用模糊PID控制将能够很好的处理这个问题，模糊PID的参数整定原理如图3所示 [12] ，被控对象是Stewart并联机构。
Figure 2. Three-dimensional model of Stewart parallel robot
图2. Stewart并联机构三维模型
Figure 3. Stewart parallel robot system with fuzzy self-tuning PID controller
图3. Stewart并联机构模糊自适应控制系统
模糊自适应PID控制器设计如下：
1) 定义输入、输出模糊集并确定个数类别
依据模糊PID控制器的控制规律以及经典PID的控制方法，同时兼顾控制精度。一般将输入的误差(e)和误差微分(ec)分为7个模糊集：NB (负大)，NM (负中)，NS (负小)，ZO (零)，PS (正小)，PM (正中)，PB (正大)。但为提高系统的响应特性，取3个模糊集N (负)，Z (零)，P (正)，因此本文模糊控制集取
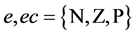(14)
输出的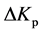
，
，
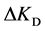也分为7个模糊集：NB (负大)，NM (负中)，NS (负小)，ZO (零)，PS (正小)，PM (正中)，PB (正大)。同样取3个模糊集
(15)
2) 确定输入输出变量的实际论域
根据控制要求，对各个输入，输出变量作如下划定：
(16)
，
，
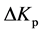的论域：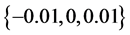
应用模糊合成推理PID参数的整定算法。第k个采样时间的整定为
(17)
式中，
，
，
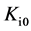为经典PID控制器的初始参数。
为了便于系统输入，输出参数映射到论域内。根据实验和相关文献，确定模糊化因子为：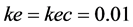
；解模糊因子为：
。
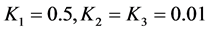3) 定义输入、输出的隶属函数
误差e、误差微分及控制量的模糊集和论域确定后，需对模糊变量确定隶属函数。即对模糊变量赋值，确定论域内元素对模糊变量的隶属度。参考输入、输出变量的变化规律，最终作如下规定：对于输入量误差(e)，误差微分(ec)都采用高斯型的隶属函数
(18)
式中，c决定函数的中心位置，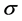
决定函数曲线的宽度。
对于输出量KP变化量(ΔKP)，KD变化量(ΔKD)，KI变化量(ΔKI)采用三角形隶属函数
(19)
式中，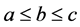
4) 确定相关模糊规则并建立模糊控制规则表
根据参数KP、KI、KD对系统输出特性的影响情况，可以归纳出系统在被控过程中对于不同的偏差和偏差变化率参数KP、KI、KD的自整定原则：
· 当偏差较大时，为了加快系统的响应速度，并防止开始时偏差的瞬间变大可能引起的微分过饱和而使控制作用超出许可范围，应取较大的KP和较小的KD。另外为防止积分饱和，避免系统响应较大的超调，KI值要小，一般取KI = 0。
· 当偏差和变化率为中等大小时，为了使系统响应的超调量减小和保证一定的响应速度，KP应取小些。
在这种情况下KD的取值对系统影响很大，应取小一些，KI的取值要适当。
· 当偏差变化较小时，为了使系统具有较好的稳态性能，应增大KP、KI值，同时为避免输出响应在设定值附近振荡，以及考虑系统的抗干扰能力，应适当选取KD。原则是：当偏差变化率较小时，KD取大一些；当偏差变化率较大时，KD取较小的值，通常为中等大小。
参考以上自整定原则，总结工程设计人员的技术知识和实际操作经验，建立合适的关于e、ec、ΔKP KP、ΔKI的模糊规则推理表如表1和表2所示。
由于微分的作用是改善系统的动态性能，对偏差进行提前预报，但微分作用强会使得响应过程提前制动，降低系统的抗干扰性能，延长调节时间，考虑到所研究Stewart并联机器人对精度、抗干扰性能要求很高，因此本文仅对PI参数进行整定。
依据图3可建立基于simulink的模糊自适应PID控制器如图4所示。
4. Stewart并联机器人控制仿真
4.1. Stewart并联机器人的控制
由前所述，伺服电机的响应速度远大于Stewart并联机器人的响应速度。在建模时将电机模型等效成比例环节，模糊PID控制器控制对象为Stewart并联机器人最终位置。为研究方便，本文选用Stewart并联机器人Z方向位置(升降方向)作为控制对象，结合图2和图4可建立Stewart并联机器人的位置控制模型如图5所示。
图5中与Admas联合的前端模块为运动学反解模块，通过数值模拟确定机器人每个位置所对应角度。
4.2. Stewart并联机器人的模糊自适应控制仿真
设PI控制参数的初始值为分别为
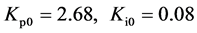(20)
基于图5建立的Stewart并联机器人模糊自适应PID控制系统仿真可得，在Z方向的阶跃响应曲线如图6所示。模糊自适应PID控制器的参数整定过程如图7所示。
设伸缩缸最短时Stewart并联机器人位置为零位。由图6可知，在Stewart并联机器人从Z = 0跃变到z = 1 m的高度时，在模糊自适应PID控制器的作用下，其阶跃响应的峰值响应时间约为0.25 s，稳态误差小于0.01 m；在传统PI控制器作用下，阶跃响应曲线的上升时间约为0.5 s，稳态时间约为0.6 s。因此模糊自适应PID控制器可以提高Stewart并联机器人位置控制性能。
图7为模糊PID控制参数随时间的变化曲线，由图7(a)可知比例系数在衰减后上升，最后稳定在2.68附近，由图7(b)可知积分参数迅速将为0，在0.05 s时迅速上升，最后稳定在0.08附近。
5. 结论
通过ADAMS建立Stewart并联机构模型和Simulink建立的模糊PID控制器联合仿真对Stewart并联机器人的控制性能进行了研究，在Stewart并联机器人从最低状态跃变到最高状态时，所给Stewart并联机器人的峰值响应时间约为0.25 s，稳态误差小于0.01 m；其模糊PID控制器的比例系数在衰减后上升，最后稳定在2.68附近，积分参数迅速将为0，在0.05 s时迅速上升，最后稳定在0.08附近。
Table 1. The value of proportion parameter
表1. 比例参数取值的模糊规则表
Table 2. The value of integral parameter
表2. 积分参数取值模糊规则表
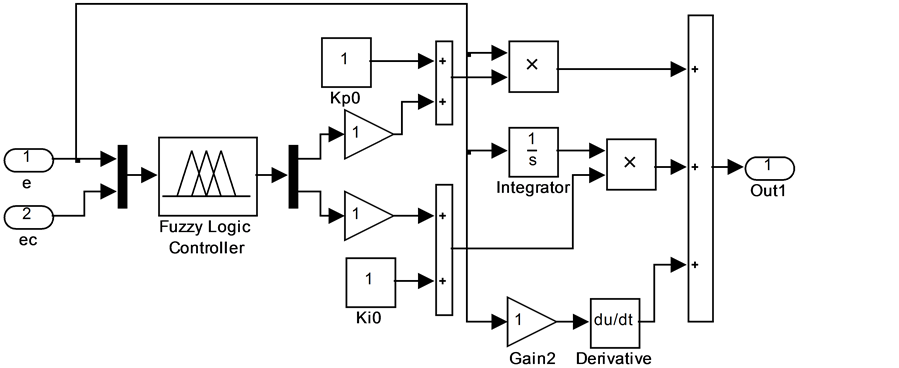
Figure 4. Fuzzy self-tuning PID controller
图4. 模糊自适应PID控制器
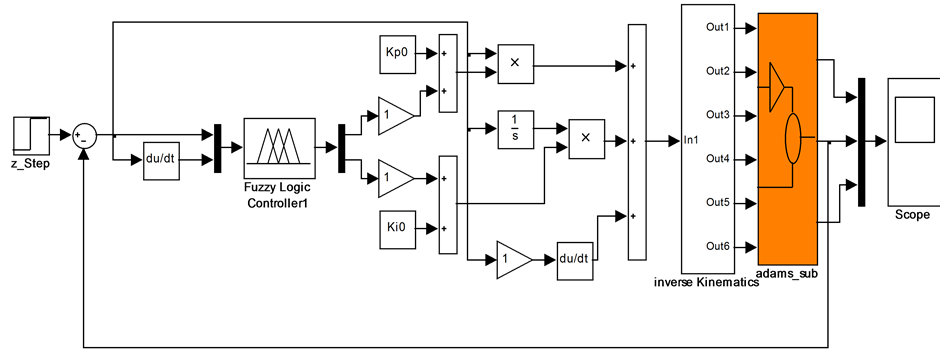
Figure 5. Simulation figure of Stewart parallel robot system with fuzzy self-tuning PID controller
图5. Stewart并联机器人的模糊自适应PID控制系统仿真图
Figure 6. Step response of Stewart parallel robot
图6. Stewart并联机器人的阶跃响应曲线
(a) 比例参数的整定曲线(b) 积分参数的整定曲线
Figure 7. Parameter of Stewart parallel robot with fuzzy self-tuning PID controller
图7. 模糊自适应PID控制的参数自整定过程
致谢
本文由河南科技大学博士科研启动费(4001-13480055)，河南科技大学青年科学基金(2015QN013)，河南科技大学2015年度大学生研究训练计划(2015006)资助。