1. 引言
在人口统计学以及精算科学中，人口死亡率预测模型一直以来都是热点问题。随时间的延续，死亡率改善导致的人口预期寿命的增加已经成为全球性趋势。死亡率预测作为养老金计划财务规划的基础，对政府养老金制度、雇主企业年金、保险公司的团体和个人养老金业务等都有重要的影响，关系到各类养老计划的财务安全和可持续发展。根据是否考虑未来死亡率变动的不确定性，把死亡率预测模型分为确定型死亡率模型(静态死亡率模型)和随机型死亡率模型(动态死亡率模型)两大类。其中，确定型死亡率模型包括Gompertz模型、Makeham模型、Weibull模型、Kannisto模型和T.N.Thile模型等，但是这些模型没有考虑死亡率的随机变动，因而不适用于死亡率的预测，只适合做模型的拟合；而随机型死亡率模型包括Lee-Carter模型、多因素年龄-时期模型、Renshaw-Haberman队列效应模型和Cairns-Blake-Dowd模型等。在随机型死亡率模型中，被公认为是随机预测方法中最典型的一个即美国人口学家Lee Ronald D和Carter Lawrence R。于1992年提出的一种预测美国未来人口死亡率变化的概率模型，该模型的优点在于人口统计模型与统计时间序列方法相结合，不需要引入能对死亡率产生影响的医疗、环境以及社会等因素，从而有效地减少了主观判断因素对于预测结果的影响，且只有时间因子一个参数需要预测，并在时间因子趋势上没有其他假设。Lee-Carter模型假设未来各个年龄组的死亡率将依据历史数据的变动情况，预测其未来趋势。此方法属于外推模型，对数表达形式和ARMA构成了Lee-Carter方法的主要特征。
在Lee-Carter模型中，对未来时间因子的预测时，用ARIMA模型，但是ARIMA模型只适合做短期预测，做中长期预测会导致误差很大，所以为了降低预测误差，可以用其它的模型来预测，本文选用广义差分模型，发现其预测误差更小。
2. 数据说明
本文采用芬兰1971~2012年男性死亡率数据。其中死亡率数据分为22组，0~5岁的分为两组0~1，1~4，其他5岁为一个组别，末组为100~104。数据来源于人口死亡率数据库(The “Human Mortality Database” at www.mortality.org)。
3. Lee-Carter模型
Lee-Carter模型的主要思路是将死亡率的变化分解为时间因子t和年龄因子x。如果用
表示x岁的人群在第t年的中心死亡率，那么
满足以下函数关系式。
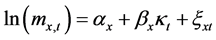(1)
其中，
反应x岁年龄组别的对数中心死亡率的平均水平，
为人口死亡率随时间变化的速度，
为年龄因子对
的敏感度，即x岁年龄组别的死亡率随着时间变化的大小，
为随机误差项，假设其服从正态分布
。为了得到唯一确定的参数估计值，加入约束条件
以及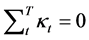
。
是为了保证参数
的平均值的含义，即
。
3.1. 模型的求解
Lee-Carter模型参数的估计方法主要包括矩阵奇异值分解法(SVD)、最小二乘(OLS)和加权最小二乘法(WLS)；奇异值分解法和最小二乘法对不同年龄人群的死亡率赋予了相同的权重，但Koissi [2] 证明了，在现实情况下，不同年龄人群对应的人口数和死亡人口数都存在较大的差异，因此这两种方法在死亡率很低的条件下使用效果较差。为此，本文采用加权最小二乘法来估计Lee-Carter模型。
加权最小二乘法通过以下两个步骤求得
，
第一步，将式(1)两边对年龄x 求和，得到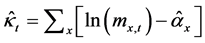
。
第二步，Wilmoth [3] 证明
的方差近似等于死亡人数
的倒数，因此可以将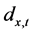
作为残差平方和的权重。最小化经加权处理后的残差平方和
，即
得到
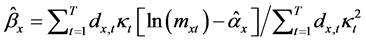[4] 。
3.2. 拟合的结果
用加权最小二乘法拟合数据，估计参数的结果如下(表1，图1)。
Table 1. Estimation results of corresponding parameters of,
表1. 相应的
，
参数的估计结果
Figure 1. The charge of estimates of 
over time
图1. 
的估计值随时间的变化
从表1中
的估计值可以看出0~1岁年龄组至70~74岁年龄组，
的估计值相对较高，75岁以上年龄组
的估计值相对较低。
表1
的估计值显示，低龄组人口(0~1岁至10~14岁)的
的估计值较高，这主要是由于新生人口具有较高的死亡率，对死亡率趋势的变化也最为敏感，高年龄组(90~94岁及以上年龄组)的估计值较低，并趋近于0，其原因在于高龄人口的死亡率特征随时间的变化较小，实际死亡率对死亡率指数不敏感。
图1给出了
的估计值随时间变化的图像，从中可以看出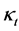
的估计值随着时间的变化呈近似线性下降的趋势，表明死亡率随时间推移而减小的速度较为稳定，与历史死亡率总体趋于下降的特征一致。
4. 模型的预测
对于未来时间因子
的预测，本文用ARIMA模型和广义差分模型。并将两者比较，选出较优的模型。
4.1. ARIMA模型
ARIMA模型是Box和Jenkins，1970年 [5] 提出的以随机理论为基础的时间序列分析方法，又称为“Box-Jenkins模型”，这一模型在经济领域的预测分析中得到广泛的应用。时间序列是依赖时间t的一组随机变量，构成该时序的单个序列值虽然具有不确定性，但对整个时间序列来说，它的变化却具有一定的规律性，可以用相应的数学模型来近似描述。一个ARIMA(p, d, q)模型，由三个过程组成：自回归模型(AR(p))，移动平均模型MA(q)，单整(I(d))。
1) 一般的p阶自回归过程AR(p)是
(2)
2) 一般的q阶的移动平均过程MA(q)可以表示为
(3)
将纯AR(p)与纯MA(q)结合得到一个一般的自回归平均过程ARMA(p, q)
(4)
3) 单整自回归移动平均过程ARIMA(p, d, q)
假设一个随机过程含有d个单位根，其经过d次差分之后，可以变换为一个平稳的自回归移动平均过程。则该随机过程称为单整自回归移动平均过程，记为ARIMA(p, d, q)。
因为
是随着时间变化，所以可以用ARIMA模型来预测未来的时间因子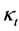
，通过比较后发现ARIMA(0, 1, 1)较合适，其预测模型为
(5)
4.2. 广义差分模型
在经济计量研究中，随机误差项自相关是一种十分普遍的现象。在这种情况下，仍应用普通最小二乘法(即OLS方法)建立的预测模型，尽管所得的结果为无偏的，但估计量不具有最小方差性，t、F检验失效，并且会使得预测置信区间增大，降低了预测精度。当然也就失去了预测的意义。如果在模型
中作广义差分变换 [6] ，得到广义差分模型即可消除自相关性从而提高预测的精度。
设线性回归模型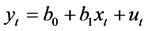
存在一阶自相关性：
，其中
为满足古典回归模型基本假定的随机误差项。将模型滞后一期，得
在方程两边同乘以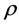
，并与原模型相减得
(6)
定义变量变换
(7)
称式(7)为广义差分变换，模型(6)可以表示成如下形式
(8)
其中，
。式(8)是经过广义差分变换得到的模型，称为广义差分模型。
4.2.1. 建立线性回归方程
从图1可以看出
与时间t近似成线性关系。所以设方程为
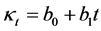，为了计算简便，把1971年作为第一年t = 1，其他的年份以此类推。用EVIEWS软件求出
，
。相应的p值都小于0.05，说明
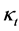与t的线性关系显著。
4.2.2. 检验自相关系
用EVIEWS将模型的残差进行拉格朗日LM乘数检验。选择滞后期为一阶。显示
，对应的P = 0.0005小于0.05，说明随机误差项存在一阶自相关。
4.2.3. 自相关修正
对线性回归模型进行广义差分变换，得出
，
，
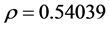，再进行LM检验，
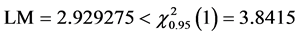，相应的P值为0.2312，说明随机误差项不存在自相关性。最后预测模型为
(9)
5. ARIMA模型与广义差分模型比较
通过计算模型拟合的平均绝对误差、平均相对误差、均方根误差、Theil不等系数、偏差比率、方差比率和协方差比率(表2)，可以明显看出，广义差分模型的拟合精度优于ARIMA模型。所以对于
的预测，选择广义差分模型。
6. 模型的预测结果检验
为评价模型的有效性，运用Lee-Carter模型预测未来3年2013，2014，2015，各年年龄段的死亡率，再求出2011~2015年5年的平均死亡率与联合国世界人口组织分布2011~2015年的死亡率作比较，如下图2。
结果显示0~60岁误差较小，60~80岁误差相对较大，而且略大于联合国世界人口组织公布的死亡率，这是因为Lee-Carter模型是用以前的数据来预测未来的，不能够准确估算出未来随着时间，医学的进步和公共卫生新技术的应用以及文化教育水平提高对死亡率的影响大小。其次高年龄组误差较大，主要是因为高年龄组死亡率不确定性较大。这些都是避免不了的。
总的来说该模型在预测未来死亡率上还是可行的。
7. 死亡率降低对养老保险金的影响
随着死亡率的降低，人口寿命的延长，越来越多的国家将会面临人口老龄化所带来的压力，芬兰也不例外。用以上Lee-Carter模型，预测2013~2022年芬兰男性婴儿的预期寿命如下图3所示。
Table 2. Comprehensive evaluation index
表2. 综合评价指标
•表示预测的死亡率，*表示联合国世界人口组织公布的死亡率
Figure 2. Comparison of mortality average predicted value and the actual value for five years among 2011-2015
图2. 2011~2015年五年死亡率平均预测值与实际值的比较
Figure 3. The change of life expectancy of male infants over time
图3. 男性婴儿预期寿命随着时间的变化
从图3中可以看出随着时间的变化，芬兰男性人口预期寿命不断地增加，到了2022年预期寿命达到了78.5岁，这就意味着，领取养老金的人会越来越多，这将会对芬兰的财政带来严峻的挑战。
不过，面对不断加剧的老龄化态势，芬兰采取多轮延迟退休，如上世纪70年代以前，芬兰人的退休年龄是60岁，1978年降至58岁，1980年降到55岁，1987年上调至60岁。2005年芬兰将退休年龄由60岁提高到63岁，身体健康且愿意继续工作的可延长至68岁。以此来缓解财政压力，并取得了一定效果。这对我国有一定的启示的作用。
因为我国同样面临预期寿命的延长带来的财政的压力，建国初的时候，我国人均预期寿命只有40岁左右，现在人均的预期寿命，“第六次全国人口普查”的数据是74.8岁。也就是说，建国60多年来，我国经济社会发展、人口数量、人口结构、人口预期寿命，都发生了巨大的变化。在建国初期制定的退休年龄政策，即1953年《劳动保险条例》规定的：女工人退休年龄是50岁，女干部55岁，男职工60岁，很显然和当前经济社会的发展不相适应，所以我国有必要像芬兰一样对退休年龄作出调整。
8. 总结
本文是用Lee-Carter模型的对芬兰男性人口死亡率进行预测。对于未来时间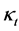
的预测，本文应用了广义差分模型。较于已有方法ARIMA模型，广义差分模型预测误差更小。最后分析了死亡率降低，对芬兰国家的财政影响，以及对我国的一些启示。